Matlab中短时傅里叶变换 spectrogram和stft的用法

  在Matlab中，做短时傅里叶变换需要使用函数spectrogram，而在Matlab2019中，引入了一个新的函数stft，下面我们就来看下这两个函数都如何使用。

  短时傅里叶变换的基本原理就是将数据分段加窗，做fft，在分段时会有overlap，因此一个向量的短时傅里叶变换结果是一个矩阵。了解了这点，下面的函数及参数就更加容易理解了。

spectrogram

参数列表

  先来看spectrogram函数，在更早期的版本中，这个函数的名字是specgram，几种常用的用法如下：

spectrogram(x)
s = spectrogram(x)
s = spectrogram(x, window)
s = spectrogram(x, window, noverlap)
s = spectrogram(x, window, noverlap, nfft)
s = spectrogram(x, window, noverlap, nfft, fs)
[s, f, t] = spectrogram(x, window, noverlap, nfft, fs)
[s, f, t] = spectrogram(x, window, noverlap, f, fs)
[s, f, t, p] = spectrogram(x, window, noverlap, f, fs)

其中，

• x表示输入信号；
• window表示窗函数，如果window的值是一个整数，那么被分段的x的每一段的长度都等于window，并采用默认的Hamming窗；如果window是一个向量，那么被分段后每一段的长度都等于length(window)，且输入的向量即为所要加的窗函数；
• overlap表示两段之间的重合点数，overlap的值必须要小于窗长，如果没有指定overlap，默认是窗长的一半，即50%的overlap；
• nfft表示fft的点数，fft的点数跟窗长可以是不同的，当没有指定该参数时，Matlab会取max(256, 2^(ceil(log2(length(window)))))，即当窗长小于256时，fft的点数是256；当窗长大于256时，fft的点数取大于窗长的最小的2的整数次幂；
• fs表示采样率，用来归一化显示使用；
• f表示显示的频谱范围，f是一个向量，长度跟s的行数相同；
  • 当x是实信号且nfft为偶数时，s的行数为(nfft/2+1)
  • 当x是实信号且nfft为奇数时，s的行数为(nfft+1)/2
  • 当x是复信号时，s的行数为nfft
  • 当在输入的参数列表中指定f后，函数会在f指定的频率处计算频谱图，返回的f跟输入的f是相同的；
• t表示显示的时间范围，是一个向量，长度跟s的列数相同；
• p表示功率谱密度，对于实信号，p是各段PSD的单边周期估计；对于复信号，当指定F频率向量时，P为双边PSD;如何计算PSD

Examples

  首先，生成信号如下，4个点频信号拼接起来：

clc;clear all;close all;
fs = 10e6;
n = 10000;
f1 = 10e3; f2 = 50e3; f3 = 80e3; f4 = 100e3;
t = (0:n-1)'/fs;
sig1 = cos(2*pi*f1*t);
sig2 = cos(2*pi*f2*t);
sig3 = cos(2*pi*f3*t);
sig4 = cos(2*pi*f4*t);

sig = [sig1; sig2; sig3; sig4];

  信号的时域波形如下：

  直接调用spectrogram(sig)，可得如下结果，图中默认横轴是频率，纵轴是时间

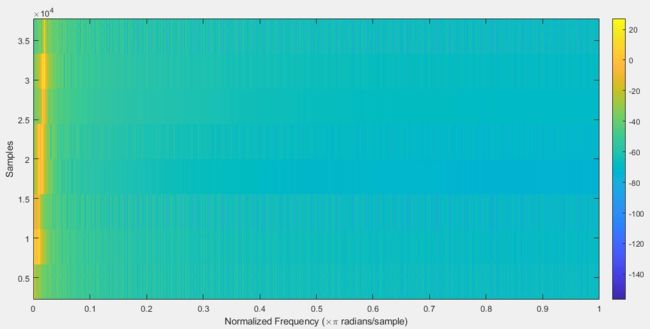
  为了绘图更灵活，我们不直接用spectrogram绘图，而且求出s后，再对s单独绘图，这次我们指定window的大小为256

s = spectrogram(sig, 256);
t = linspace(0, 4*n/fs, size(s,1));
f = linspace(0, fs/2, size(s,2));
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;

  noverlap默认是50%，现在我们把它设为window的长度减1，即每次的步进为1

s = spectrogram(sig, 256, 255);
t = linspace(0, 4*n/fs, size(s,1));
f = linspace(0, fs/2, size(s,2));
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;

  再加上nfft和fs参数，我们指定fft点数就是窗长

s = spectrogram(sig, 256, 128, 256, fs);

  这个的图形跟之前一样，不再画了

  如果在返回值中，增加f和t，这样我们下面就不用再重新定义f和t了

[s, f, t] = spectrogram(sig, 256, 128, 256, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;

  从上面的图中我们可以看出，我们的4个信号的频率都比较小，而画出来的图显示的频谱范围比较大，导致下面很大一部分信息我们其实都不需要。这时，我们就可以通过指定f的区间来计算频谱。为了显示效果更好，我们把其他参数也调一下

window = 2048;
noverlap = window/2;
f_len = window/2 + 1;
f = linspace(0, 150e3, f_len);
[s, f, t] = spectrogram(sig, window, noverlap , f, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;

  最后再把功率谱密度的返回值加上

[s, f, t, p] = spectrogram(sig, window, nfft, f, fs);
figure;
imagesc(t, f, p);xlabel('Samples'); ylabel('Freqency');
colorbar;

stft

  这个函数在Matlab的解释并不是很多，example也只写了两个，但用法比较简单：

window = 2048;
noverlap = window/2;
nfft = window;
[s, f, t, p] = spectrogram(sig, window, noverlap, nfft, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
title('使用spectrogram画出的短时傅里叶变换图形');
colorbar;

ss = stft(sig,fs,'Window',hamming(window),'OverlapLength',window/2,'FFTLength',nfft);
figure;
imagesc(t, f, 20*log10((abs(ss(1024:end,:)))));xlabel('Samples'); ylabel('Freqency');
title('使用stft画出的短时傅里叶变换图形');
colorbar;

欢迎关注微信公众号：