带有滤波器的数字pid控制matlab实现

前言：这一部分分为两个部分，首先介绍基于低通滤波器的信号处理，第二部分才是带有滤波器的数字pid控制matlab实现以及老规矩最后用simulink实现一下

---

一、基于低通滤波器的信号处理

低通滤波器为：Q（s）=1/（0.04s+1）
因为为离散系统，所以要将这个离散化，方法还是用c2d函数，只不过用的参数不在是zoh，而是使用tucsin。
直接上代码，代码很简单，说明都在注释里面：

clear all;
close all;

ts = 0.001; %采样周期
sys=tf([1],[0.04,1]); %滤波器模型
dsys = c2d(sys,ts,'tucsin');%模型离散化
[num,den]=tfdata(dsys,'v');


%获取输入
for k=1:1:5000
    time(k)=k*ts; 
    noise(k)=0.1*sin(100*2*pi*k*ts); %信号里面的高频噪声
    yinput(k)=noise(k)+0.5*sin(0.4*pi*k*ts); %混合信号
end

yout_1=0;
yinput_1=0;

for i=1:1:5000
    yout(i) = -den(2)*yout_1+num(1)*yinput(i)+num(2)*yinput_1;%滤波
    
    %更新状态
    yout_1=yout(i);
    yinput_1=yinput(i);
end

subplot(211);
plot(time,yinput,'k','linewidth',2);
subplot(212);
plot(time,yout,'k','linewidth',2);

结果：

---

二、带有滤波器的数字pid控制

被控对象模型为：G(s)=523500/(s^3 + 87.35s^2+10470s)
滤波器模型为：Q（s）=1/（0.04s+1）
噪声加在对象模型输出端，采样时间为1ms
程序中M的值用于选择选择是否用滤波器，是否加噪声。
% m=1：不加噪声
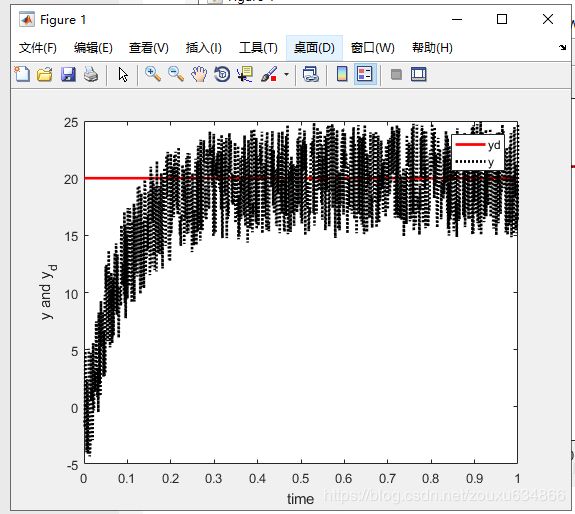
% m=2：加噪声不加滤波器
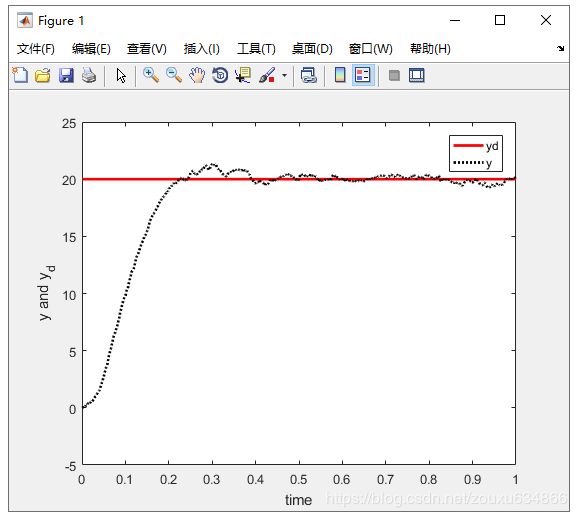
% m=3：加噪声加滤波器

代码：

clear all;
close all;

%获取控制对象离散化模型
ts = 0.001;  %采样时间
sys = tf([523500],[1,87.35,10470,0]);
dsys = c2d(sys,ts,'zoh');
[num,den]=tfdata(dsys,'v');

%获取滤波器离散化模型
sys1=tf([1],[0.04,1]); %滤波器模型
dsys1 = c2d(sys1,ts,'tucsin');%模型离散化
[num1,den1]=tfdata(dsys1,'v');
 y_filter_out_1=0;
 y_noise_1=0;


%设置pid参数
k_p=0.2;
k_i=0.05;

%设置输入信号形式
y_d = 20*ones(1,1000);   %输入信号为阶跃信号 
%y_d = [ones(1,250) zeros(1,250)]; 输入信号为阶跃信号
% for k=1:1:500%输入信号为正弦信号
% y_d(k) = 0.5*sin(4*pi*k*ts); 
% end


%噪声信号
for j=1:1:1000
    noise(j)=5*rands(1); %信号里面的高频噪声
end


y = zeros(1,1000);%初始化输出信号
y_noise=zeros(1,1000);
y_feed=zeros(1,1000);%反馈回来的信号，y_feed=y
 y_filter_out=zeros(1,1000);
erro = zeros(1,1000);%信号差值
erro_1 = 0;%上一时刻信号差值
erro_total = 0;%信号差值累计值
y_1=0;%上一时刻的输出
y_2=0;%上一上一时刻的输出
y_3=0;%上一上一上一时刻的输出

pi_out=0;  %pid控制器的输出，注意不是系统输出
pi_out_1=0;%上一时刻pid控制器的输出，注意不是系统输出
pi_out_2=0;%上一上一时刻pid控制器的输出，注意不是系统输出
pi_out_3=0;%上一上一上一时刻pid控制器的输出，注意不是系统输出



% m用来选择是否用滤波器，是否加噪声。
% m=1：不加噪声
% m=2：加噪声不加滤波器
% m=3：加噪声加滤波器
M=input('input the m:');

beta=1;

if M==1
    for k=1:1:1000
    time(k)=k*ts;  %存储时间，用于后面画图
 
    y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3;%控制对象 
     y_feed(k)= y(k);
    
    erro(k) =y_d(k) -  y_feed(k) ;

    if  abs(erro(k))<=0.8
        erro_total = erro_total +erro(k) ;
    end
    
    if  abs(erro(k))>0.8
       erro_total = 0 ;
    end
    
    pi_out = erro(k) *k_p+k_i*erro_total*ts;
       
   %更新系统输出状态
   y_3=y_2;
   y_2=y_1;
   y_1=y(k);
    
  %更新pid输出状态
    pi_out_3=pi_out_2;
    pi_out_2=pi_out_1;
    pi_out_1=pi_out;
    
    end

    %画图
    plot(time,y_d,'r',time,y,'k:','linewidth',2);
    xlabel('time');
    ylabel('y and y_d');
    legend('yd','y');
end


if  M==2
    for k=1:1:1000
    time(k)=k*ts;  %存储时间，用于后面画图
 
    y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3 ;%控制对象 
     
     y_feed(k)= y(k)+noise(k); %注意：噪声是加载对象模型输出上的，而不是麽模型内部，模型本身的输出是正确的，只是加上了噪声后作为整个系统的输出。所以+noise(k)不能写在上面的后面
    
    erro(k) =y_d(k) -  y_feed(k) ;

    if  abs(erro(k))<=0.8
        erro_total = erro_total +erro(k) ;
    else
       erro_total = 0 ;
    end
    pi_out = k_p*erro(k) +k_i*erro_total*ts;
       
   %更新系统输出状态
   y_3=y_2;
   y_2=y_1;
   y_1=y(k);
    
  %更新pid输出状态
    pi_out_3=pi_out_2;
    pi_out_2=pi_out_1;
    pi_out_1=pi_out;
    
    end

    %画图
    plot(time,y_d,'r',time,y_feed,'k:','linewidth',2);
    xlabel('time');
    ylabel('y and y_d');
    legend('yd','y');
end

if  M==3
    for k=1:1:1000
    time(k)=k*ts;  %存储时间，用于后面画图
 
    y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3 ;%控制对象
    y_noise(k)= y(k)+noise(k);
    y_filter_out(k) = -den1(2)*y_filter_out_1+num1(1)*y_noise(k)+num1(2)*y_noise_1;
    
    y_feed(k)=y_filter_out(k);%注意：噪声是加载对象模型输出上的，而不是麽模型内部，模型本身的输出是正确的，只是加上了噪声后作为整个系统的输出。所以+noise(k)不能写在上面的后面
    
    erro(k) =y_d(k) -  y_feed(k) ;

    if  abs(erro(k))<=0.8
        erro_total = erro_total +erro(k) ;
    else
       erro_total = 0 ;
    end
    pi_out = k_p*erro(k) +k_i*erro_total*ts;
       
    
    %更新滤波器输出状态
    y_filter_out_1=y_filter_out(k);
    y_noise_1=y_noise(k);

   %更新系统输出状态
   y_3=y_2;
   y_2=y_1;
   y_1=y(k);
    
  %更新pid输出状态
    pi_out_3=pi_out_2;
    pi_out_2=pi_out_1;
    pi_out_1=pi_out;
    
    end

    %画图
    plot(time,y_d,'r',time,y_feed,'k:','linewidth',2);
    xlabel('time');
    ylabel('y and y_d');
    legend('yd','y');
end

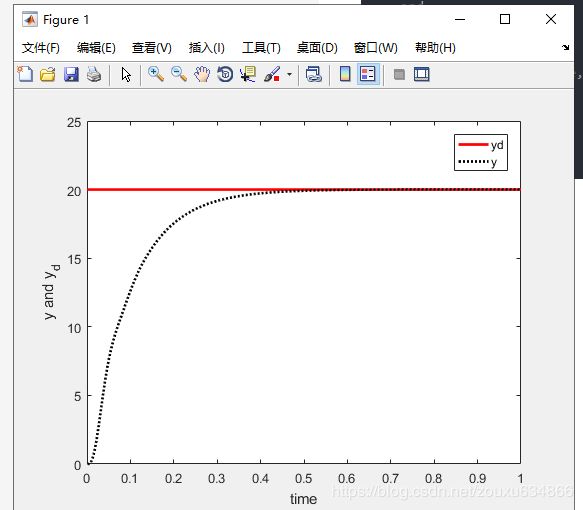
仿真结果：
没有噪声：

家噪声不加滤波器：

加噪声加滤波器：

说明：
1.这段程序中使用了积分分离pid，但要注意当差值小于阈值时才引入积分，另外累计差值是在引入积分时才开始算，前面未引入积分时的差值不能在在后面加上！！！比如当k=6时引入积分，此时erro_total从此时才开始算，之前k《=5的差值erro不能算。
2.搞清楚哪个是对象模型输出哪个是系统输出，加了噪声后为系统输出，是要反馈回去的。另外噪声并不影响对象模型，对象模型的差分方程y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3中的y(k)、y_1、y_2、y_3均为对象模型的输出，千万不要将加了噪声的系统输出当做这里面的y_1、y_2、y_3带进去计算，我在这里就犯了错，我将对象模型的差分方程写成了y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3+noise(k)显然这事错的，因为这么写的话就表示对象模型的输出与噪声有关，这事错的，噪声是在模型外部，只影响下一个模型（比如滤波器）的输入，但不会影响对象模型的输出。所以应该像上面程序中写的那样：

y(k) = -den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*pi_out_1+num(3)*pi_out_2+num(4)*pi_out_3 ;%控制对象 
     
y_feed(k)= y(k)+noise(k); %注意：噪声是加载对象模型输出上的，而不是麽模型内部，模型本身的输出是正确的，只是加上了噪声后作为整个系统的输出。所以+noise(k)不能写在上面的后面
    
erro(k) =y_d(k) -  y_feed(k) ;

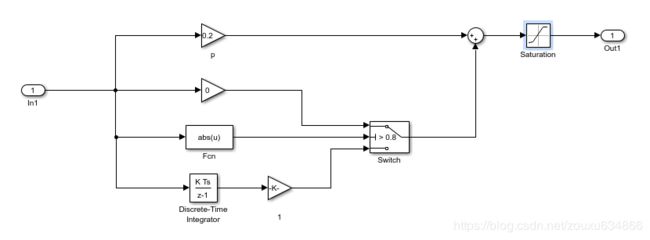
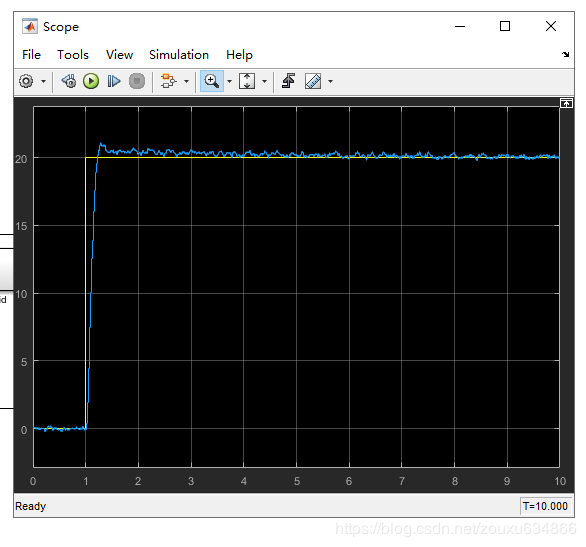
三、simulnik仿真

可以看出效果还是可以的。