朴素贝叶斯分类器

一、实验目的
1、 用朴素贝叶斯分类器完成对未知样本的类型分类
二、 实验内容：
1、 实验题目：设某网球俱乐部由下表给出的打球与气候情况的历史数据样本集S。

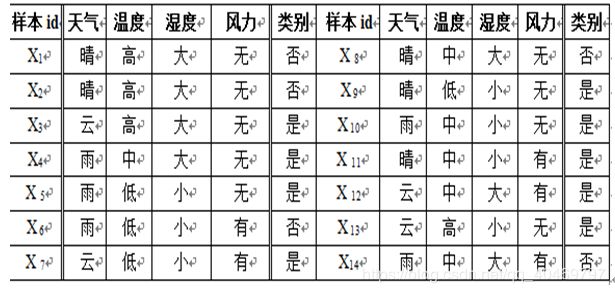
俱乐部计划后天安排一次网球比赛活动，而后天的天气预报情况如下：
Z=(天气=“晴”，温度=“高”，湿度=“小”，风力=“无”) 根据历史样本集S，利用朴素贝叶斯分类器，判断后天是否适宜进行网球比赛

过程代码

#include "stdio.h"

//天气
enum enum_outlook
{
	sunny = 0,
	overcast = 1,
	rain = 2
}_outlook;

//温度
enum enum_temperature
{
	hot = 0,
	mild = 1,
	cool = 2
}_temperature;

//湿度
enum enum_humidity
{
	high = 0,
	normal = 1,
}_humidity;

//风力 
enum enum_wind
{
	weak = 0,
	strong = 1
}_wind;

//类别 
enum enum_targetAttribute
{
	yes = 0,
	no = 1
}_targetAttribute;


#define TRAIN_NUM 14      //定义14个训练实例
#define ATTR_NUM 4        //每个训练实例有4个属性
//初始化训练实例 
int trainSample[][ATTR_NUM + 1] = {
	{
		sunny,hot,high,weak,no
	},
	{
		sunny,hot,high,weak,no
	},
	{
		overcast,hot,high,weak,yes
	},
	{
		rain,mild,high,weak,yes
	},
	{
		rain,cool,normal,weak,yes
	},
	{
		rain,cool,normal,strong,no
	},
	{
		overcast,cool,normal,strong,yes
	},
	{
		sunny,mild,high,weak,no
	},
	{
		sunny,cool,normal,weak,yes
	},
	{
		rain,mild,normal,weak,yes
	},
	{
		sunny,mild,normal,strong,yes
	},
	{
		overcast,mild,high,strong,yes
	},
	{
		overcast,hot,normal,weak,yes
	},
	{
		rain,mild,high,strong,no
	},
};

int newSanple[ATTR_NUM] = { sunny,cool,high,strong };                             //定义需要分类的新实例
float preP[ATTR_NUM] = { (float)0.333,(float)0.333,(float)0.50,(float)0.50 };     //m-估计每个属性对应的先验概率

#define m TRAIN_NUM                                                                //m-估计的m值等于训练样例数
                                                           
void CalcposAndNegNum(int*pPosNum, int*pNegNum)
{
	int i;

	*pPosNum = 0;
	*pNegNum = 0;
	for (i = 0; i<TRAIN_NUM; i++)
	{
		if (trainSample[i][ATTR_NUM] == yes)
		{
			(*pPosNum)++;
		}
		else
		{
			(*pNegNum)++;
		}
	}
	
	return;
}

//朴素贝叶斯分类器 
void NaiveBayes(void)
{
	int x;
	for (int i = 0; i <ATTR_NUM; i++)
	{
	scanf("%d", &newSanple[i]);
	}

	int j, cntY, cntN;
        //存储训练样例目标属性为yes或no的样本数
	int posNum, negNum;
        //存储目标值yes和no的概率
	float PVyes, PVno, PVyesTemp, PVnoTemp;
        //存储目标值为yes时需分类的每个属性的概率
	float PAttrYes[ATTR_NUM];
        //存储目标值为no时需分类的每个属性的概率
	float PAttrNo[ATTR_NUM];
        //计算训练样例集的正样本数和负样本数
	CalcposAndNegNum(&posNum, &negNum);
        //计算目标值 yes 的概率
	PVyes = (float)posNum / (float)TRAIN_NUM;
        //计算目标值 no 的概率
	PVno = (float)negNum / (float)TRAIN_NUM;
        printf("目标值概率PVyes=%f\n\n",PVyes);
	printf("目标值概率PVno=%f\n\n", PVno);
        //计算目标值分别为 yes 和 no 时各个需分类属性对应的概率
	for (j = 0; j<ATTR_NUM; j++)
	{
                //清 0 计数变量
		cntY = 0;
		cntN = 0;
		for (int i = 0; i<TRAIN_NUM; i++)

		{
                        //统计目标值为 yes 时各个需分类的属性在训练样例中的个数
			if (trainSample[i][ATTR_NUM] == yes)
			{
                                //如果训练样例的目标属性是 yes
                                //且该训练样例的属性值和需要分类的样例的属性值相等,则计数 
				if (trainSample[i][j] == newSanple[j])
				{
					cntY++;
				}
			
			}
                        //统计目标值为 no 时各个需分类的属性在训练样例中的个数

			else if (trainSample[i][ATTR_NUM] == no)
			{
                                //如果训练样例的目标属性是 no
                                //且该训练样例的属性值和需要分类的样例的属性值相等,则计数
				if (trainSample[i][j] == newSanple[j])
				{
					cntN++;
				}
			}
		}
		printf("统计输入样例属性下Yes的个数cntY=%d\n\n",cntY);
		printf("统计输入样例属性下No的个数cntN=%d\n\n",cntN);
	 
                //计算目标值为 yes 时需分类的各个属性的概率
                PAttrYes[j] = ((float)cntY + (float)m*preP[j]) / ((float)(posNum + m));
                //计算目标值为 no 时需分类的各个属性的概率
		PAttrNo[j] = ((float)cntN + (float)m*preP[j])/((float)(negNum + m));
		printf("目标值为Yes时输入属性的概率:%f\n\n",PAttrYes[j]);

		printf("目标值为No时输入属性的概率:%f\n\n",PAttrNo[j]);
	}
        //分别计算需要分类的样例的目标值为 yes 和 no 的概率
	for (int i = 0; i<ATTR_NUM; i++)
	{
		PVyes = PVyes*PAttrYes[i];
		PVno = PVno*PAttrNo[i];
	}
	printf("概率PVyes=%f\n\n",PVyes);
	printf("概率PVno=%f\n\n",PVno);
        //做归一化处理
	PVyesTemp = PVyes / (PVyes + PVno);
	PVnoTemp = PVno / (PVyes + PVno);
	printf("归一化后实例被分为yes的概率:%f\n\n", PVyesTemp);
	printf("归一化后实例被分为no的概率:%f\n\n", PVnoTemp);
	if (PVyesTemp>PVnoTemp)
	{
		printf("所以实例被分类为:yes\n\n");

	}
	else
	{
		printf("所以实例被分类为:no\n");
	}
	return;
}
//主函数
int main(void)
{
    printf("请输入样例属性:\n");
       //调用朴素贝叶斯学习器算法 
	NaiveBayes();
	return 1;
}

朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。