聚类之Mean Shift算法

前言

  上篇博客说到了K-Means算法的不足之一，由此介绍了K-Means++算法来优化初始聚类中心的选择。本篇博客将介绍Mean Shift算法，来解决K-Means算法的另一个不足之处。
  Mean Shift算法，又被称为均值漂移算法。与K-Means算法不同的是，它不需要事先指定类别个数$k$，其聚类中心是通过在给定区域中的样本的均值来确定的，通过不断更新聚类中心，直至最终的聚类中心不再改变为止。

1. Mean Shift向量

  对于给定的$n$维空间$R^n$中的$m$个样本点$X^{(i)},i=1,\dots ,m$，对于其中的一个样本$X$，其Mean Shift向量为：
$$M_h(X)=\frac{1}{k}\sum _{X^{(i)}\in S_h}(X^{(i)}-X)$$  其中，$S_h$指的是一个半径为$h$的高维球区域，其定义如下：$$S_h(x)=\left(y\right|(y-x)(y-x{)}^T\le h^2)$$  在二维平面上来看，$S_h$是一个半径为$h$的圆，其中有多个样本点。在计算均值漂移向量的过程中，通过计算圆$S_h$中的每一个样本点$X^{(i)}$相对于点$X$的偏移向量$(X^{(i)}-X)$，再对所有的均值漂移向量求和，最后再求平均，即最上面的公式。
  但是在上述的计算过程中存在一个问题，即在$S_h$的区域内，每一个样本点$X^{(i)}$对样本$X$的贡献（权重）是一样的，而实际上，每一个样本点$X^{(i)}$对样本$X$的贡献是不一样的。因此，引入核函数来度量这样的贡献。

  通常，可以取$S_h$为整个数据集范围。

2. 核函数

  引入核函数，可以使得随着样本与被漂移点的距离不同，其漂移量对均值漂移向量的贡献也不同。核函数的定义如下：
  设$\aleph$是输入空间（欧式空间$R^n$的子集或离散集合），$H$为特征空间（希尔伯特空间），如果存在一个$\aleph$到$H$的映射：
$$\varphi (x):\aleph \to H$$  使得所有$x_1,x_2\in \aleph$，函数$K(x_1,x_2)$满足条件：
$$K(x_1,x_2)=\varphi (x_1)\cdot \varphi (x_2)$$  则称$K(x_1,x_2)$为核函数，$\varphi (x)$为映射函数，$\varphi (x_1)\cdot \varphi (x_2)$为$\varphi (x_1)$和$\varphi (x_2)$的内积。

  核函数其实就是表示低维空间里数据的内积映射到高维空间里后的内积，在低维空间线性不可分的样本映射到合适的高维空间就变得线性可分。具体的内容我准备放在另外一篇博客里细说，这里就简单提一下。

  高斯核函数是使用较多的一种核函数，其函数形式为：
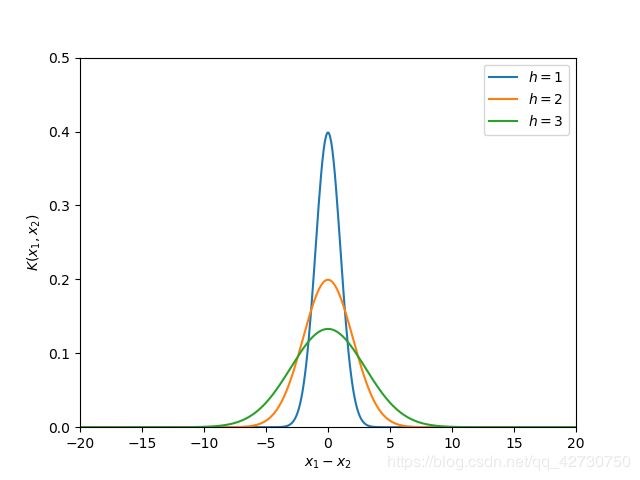$$K\left(\frac{x_1-x_2}{h}\right)=\frac{1}{\sqrt{2\pi }h}exp(-\frac{(x_1-x_2{)}^2}{2h^2})$$  一维高斯函数大致就是这个样子：  当带宽$h$一定时，样本点之间的距离越近，其核函数的值越大；当样本点之间的距离相等时，随着高斯核函数的带宽$h$的增大，核函数的值在减小。

3. 算法原理

  引入核函数后的Mean Shift向量就变为了下面这种形式：
$$\begin{array}{rl}{M}_h(X)& =\frac{{\sum }_{X^{(i)}\in S_h}\left[K\right(\frac{X^{(i)}-X}{h})\cdot (X^{(i)}-X\left)\right]}{{\sum }_{X^{(i)}\in S_h}\left[K\right(\frac{X^{(i)}-X}{h}\left)\right]}\\ & =\frac{{\sum }_{X^{(i)}\in S_h}\left[K\right(\frac{X^{(i)}-X}{h})\cdot X^{(i)}]}{{\sum }_{X^{(i)}\in S_h}\left[K\right(\frac{X^{(i)}-X}{h}\left)\right]}-X\end{array}$$   其中，$K\left(\frac{X^{(i)}-X}{h}\right)$是高斯核函数。
  在Mean Shift算法中，通过迭代的方式找到最终的聚类中心，即对每一个样本点计算其漂移均值，以计算出来的漂移均值点作为新的起点，重复以上过程，直到满足终止条件，得到的最终的均值漂移点即为最终的聚类中心。
  具体步骤如下：

• 在指定的区域内计算每一个样本点的漂移均值；
• 移动该点到漂移均值点处；
• 重复上述的过程，不断计算新的漂移均值、移动；
• 当满足最终的条件时（漂移点与该点距离小于一个很小值），结束迭代。

  下面用一个图说一下：
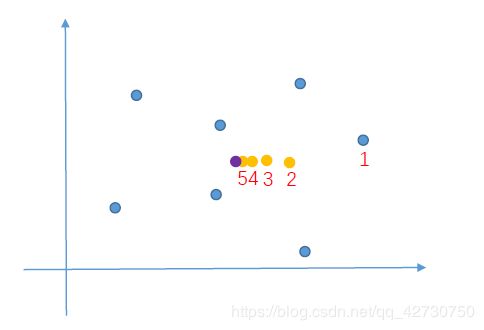  先选择一个样本点（1号样本点），然后计算1号样本点与所有样本点的漂移均值，得到2号点，然后计算2号点与1号点的距离，当距离小于$1\times 10^{-6}$时，这个点不在漂移，然后再计算区域内的其他样本点，计算完毕即一次迭代结束；然后进行第二次迭代，这时的1号样本点已经漂移到了2号点，然后再计算2号样本点与所有样本点的漂移均值，得到3号点，然后计算3号点与2号点之间的距离，这样不断计算、迭代，最终1号点漂移到了5号点。

4. 代码实现

import numpy as np
import matplotlib.pyplot as plt
import math


def load_data(file_path):
    data_list = []
    with open(file_path, 'r') as f:
        lines = f.readlines()
        for line in lines:
            data_row = []
            line = line.strip().split('\t')
            for x in line:
                data_row.append(float(x))
            data_list.append(data_row)
    data_arr = np.array(data_list)
    return data_arr


def o_distance(vecA, vecB):
    distance = math.sqrt(np.dot((vecA - vecB), (vecA - vecB)))
    return distance


def gaussian_kernel(distance, bandwidth):
    """
    高斯核函数
    :param distance: 欧氏距离(mat)
    :param bandwidth: 带宽h(int)
    :return: 高斯函数值
    """
    # 样本个数
    dim_m = np.shape(distance)[0]
    right = np.array(np.zeros(shape=(dim_m, 1)))
    for i in range(dim_m):
        right[i] = np.exp(
            (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth)
        )
    left = 1 / (bandwidth * math.sqrt(2 * math.pi))

    gaussian_value = left * right
    return gaussian_value


def shift_point(point, points, bandwidth):
    """
    计算均值漂移点
    :param point: 需要计算的点
    :param points: 所有样本点
    :param bandwidth:
    :return: 漂移后的点
    """
    # 样本个数
    dim_m, dim_n = np.shape(points)

    # 计算距离
    distances = np.array(np.zeros(shape=(dim_m, 1)))
    for i in range(dim_m):
        distances[i] = o_distance(point, points[i])

    # 计算高斯核
    weights = gaussian_kernel(distances, bandwidth)

    # 计算分母
    all_sum = 0.0
    for i in range(dim_m):
        all_sum += weights[i]

    # 计算均值漂移
    shift_value = np.dot(weights.T, points) / all_sum

    return shift_value[0]


def label_points(data_arr):
    """
    计算样本点所属的类别
    :param data_arr_shift:
    :return:
    """
    data_arr = np.around(data_arr, decimals=4)
    cluster_centers = []
    label_dict = {}
    label_list = []
    label = 0
    for data in data_arr:
        temp = str(data)
        if temp not in label_dict:
            label_dict[temp] = label
            label_list.append(label)
            label += 1
            cluster_centers.append(data)
        else:
            label_ = label_dict.get(temp)
            label_list.append(label_)

    labels = np.asarray(label_list)
    cluster_centers = np.asarray(cluster_centers)

    return labels, cluster_centers


def train_mean_shift(data_arr, bandwidth=2):
    """
    训练Mean Shift模型
    :param points: 特征数据
    :param bandwidth:
    :return:
    """
    mean_shift_points = np.copy(data_arr)
    max_distance = 1
    iteration = 0
    dim_m = np.shape(data_arr)[0]
    # 标记是否需要漂移
    flag = [True] * dim_m

    # 计算均值漂移向量
    while max_distance > 1e-6:
        max_distance = 0
        for i in range(dim_m):
            # 判断每一个样本点是否需要计算漂移均值
            if not flag[i]:
                continue
            # 初始样本点
            point_shift = mean_shift_points[i]
            point_start = point_shift
            # 样本点漂移
            point_shift = shift_point(point_shift, data_arr, bandwidth)
            # 漂移后的点与样本点之间的距离
            distance_shift = o_distance(point_shift, point_start)
            if distance_shift > max_distance:
                max_distance = distance_shift
            if distance_shift < 1e-6:
                flag[i] = False

            mean_shift_points[i] = point_shift
        iteration += 1
        print('iteration: %d' % iteration)

    # 计算最终的所属类别
    labels, cluster_centers = label_points(mean_shift_points)
    return labels, cluster_centers


def draw_picture(data_arr, cluster_centers, labels):
    dots1 = data_arr[labels == 0]
    dots2 = data_arr[labels == 1]
    dots3 = data_arr[labels == 2]
    dots4 = data_arr[labels == 3]

    plt.figure()
    plt.scatter(dots1[:, 0], dots1[:, 1], marker='o',
                color='#1f77b4', alpha=0.7, label='dots1 samples')
    plt.scatter(dots2[:, 0], dots2[:, 1], marker='o',
                color='#ff7f0e', alpha=0.7, label='dots2 samples')
    plt.scatter(dots3[:, 0], dots3[:, 1], marker='o',
                color='#2ca02c', alpha=0.7, label='dots3 samples')
    plt.scatter(dots4[:, 0], dots4[:, 1], marker='o',
                color='purple', alpha=0.7, label='dots4 samples')
    plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], marker='x',
                color='black', alpha=0.7, label='centroids')
    plt.savefig('./result.png')
    plt.show()


if __name__ == '__main__':
    file_path = './data.txt'

    data_arr = load_data(file_path)
    labels, cluster_centers = train_mean_shift(data_arr, bandwidth=2)
    draw_picture(data_arr, cluster_centers, labels)

  运行结果如下图所示：
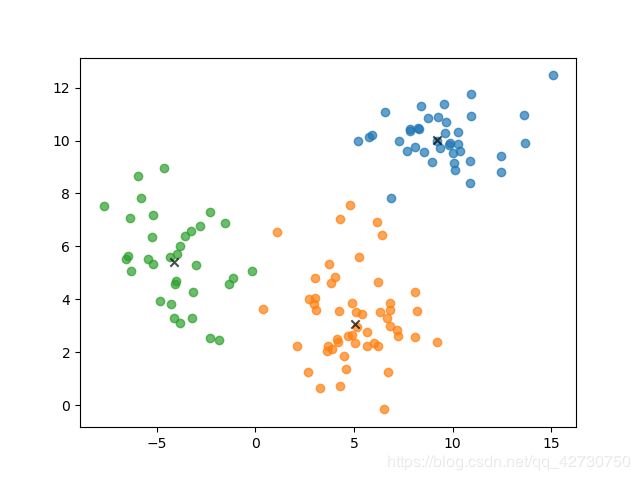  可以看到Mean Shift算法自动将样本聚类成了3个类，效果还可以，另外，我将书本上的代码进行了优化，迭代速度明显提升了许多。

  在实际测试过程中，$k$的具体取值要不断地去尝试，找到一个合适的$k$才会有好的聚类效果。

结束语

  昨天晚上考完最后一门课，大三生活正式结束，又回到了考研日常。本来计划花一点时间写下这篇博客，结果没想到花了大半个晚上，程序迭代了上万次，结果就是无法收敛了，最终发现了端倪——没区分深拷贝与浅拷贝，这次算是记住了o(╥﹏╥)o，改正后程序很快地迭代20多次就收敛了，很nice (=￣ω￣=)喵了个咪。