梯度下降算法原理python实现，更易理解

梯度下降

要找到某个函数的最小值，就是沿着该函数的梯度的负方向寻找。若寻找某函数最大值，则沿着梯度方向找。

那么梯度下降数学表示：

：步长或叫学习率，：是函数关于w的导数

梯度上升数学表示：

上述某函数可以理解成最小二乘问题（线性回归和非线性）的损失函数，均方误差损失表示为：

对于凸函数可以使用最小二乘法求解最优点，过程是求关于w的导数，使导数等于0即可

对于梯度下降法则需要迭代N次，每次将wi带入上式中求得wi值下的导数，然后求得wi+1的值

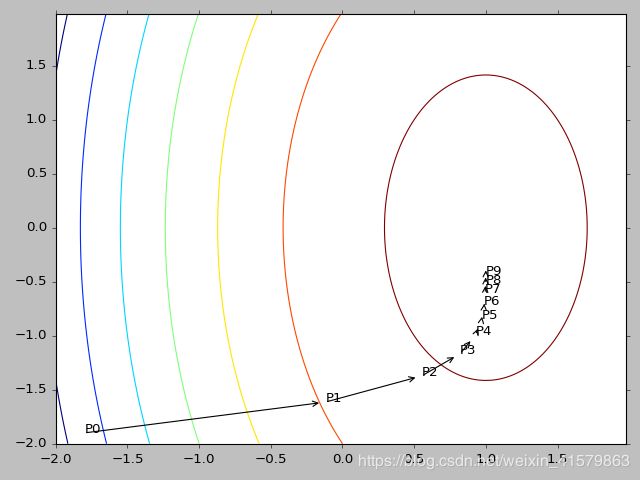
看图理解

上图是梯度下降求解过程，假设求解一个线性回归问题，目标函数是均方误差最小，数学公式表示为：

用矩阵表示为：，其中X已知，y已知，w是求要的参数，圆心视为最优点也是误差最小点，那么对w求导

则梯度的负方向寻找最小点，p0是开始位置，w0可以使初始值1的矩阵，则将w0带入导数方程求得w0导数，那么根据梯度下降法

，根据此方法一直迭代的圆心点附近，求得的wi使得均方误差最小。

实例

首先生成随机样本：

x = np.arange(0, 100, 1)
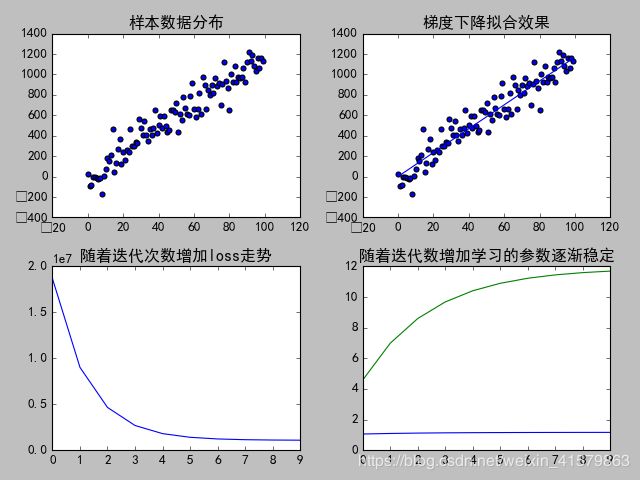
y = x * 11.8 - np.random.standard_normal(100) * 100

使用梯度下降法求解结果如下图

第一张图表示样本分布，第二张（右上）表示使用梯度下降法求解拟合直线，第三张（左下）表示随着迭代次数增加模型损失逐渐下降直至平稳，第四张图表示参数的学习效果，随着迭代次数增加参数学习逐渐稳定。

迭代 1 损失：18659840.76439424,weight参数：[[1.0539232487566108, 4.578364388994817]]
迭代 2 损失：9004152.836684883,weight参数：[[1.0901282014628215, 6.981505910781841]]
迭代 3 损失：4649307.430631565,weight参数：[[1.1144339831409158, 8.5953966993742]]
迭代 4 损失：2685213.4523903765,weight参数：[[1.13074857483731, 9.679246133912951]]
迭代 5 损失：1799380.5932514765,weight参数：[[1.1416964803735679, 10.407132849392006]]
迭代 6 损失：1399858.0328088128,weight参数：[[1.1490402518776508, 10.89596376971111]]
迭代 7 损失：1219667.972099556,weight参数：[[1.1539635759490037, 11.22425070567449]]
迭代 8 损失：1138399.8251730944,weight参数：[[1.157261387354931, 11.44472025576014]]
迭代 9 损失：1101746.7947403109,weight参数：[[1.1594675447067935, 11.59278230490871]]
迭代 10 损失：1085215.783217484,weight参数：[[1.1609405742996355, 11.692217259740454]]

迭代10轮，直线方程可以表达为y =  11.692217259740454* x +1.1609405742996355和样本生成方程即（y = x * 11.8 - np.random.standard_normal(100) * 100）比较接近了

python实现代码如下

# @Time : 2020/6/16 19:42
# @Author : 大太阳小白
# @Software: PyCharm
"""
通过程序理解如何使用梯度下降求解
1、首先程序定义一个样本集，用来代替真实数据的分布
2、计算模型误差，使用均方误差
3、利用均方误差求导，解出关于待定参数w的导数
4、目标函数是误差最小，则关于w的方程求w下降最快方向使目标函数下降最快
5、定义w初始位置，带入导数方程，求得关于初始位置w的导数
6、w根据w位置导数移动lamda倍步长，得到新的w1点，带入导数方程求w1导数，如此迭代
7、当满足一定迭代限制或是误差限制时停止迭代，求得w值
"""
import numpy as np
import matplotlib.pyplot as plt


def create_sample_set():
    """
    生成样本数据集
    :return:
    """
    x = np.arange(0, 100, 1)
    y = x * 11.8 - np.random.standard_normal(100) * 100
    return x, y


def loss(weight, x, y):
    """
    损失函数使用均方误差
    :param weight:权重
    :param x:
    :param y:
    :return:
    """
    return (x * weight - y).T * (x * weight - y)


def gradient(weight, x, y):
    """
    基于损失函数求关于w的导数
    :param weight:
    :param x:
    :param y:
    :return:
    """
    return x.T * (x * weight - y)


def gradient_descent(x, y, max_iter=10, learning_rate=0.001):
    """
     梯度下降求解
    :param x:
    :param y:
    :param max_iter:
    :param learning_rate:
    :return:
    """
    m, n = np.shape(x)
    weight = np.mat(np.ones((n, 1)))
    loss_arr = []
    weight_arr = np.zeros((max_iter,n))
    for i in range(max_iter):
        g = gradient(weight, x, y)
        weight = weight - learning_rate * g
        error = loss(weight, x, y).T.tolist()[0][0]
        loss_arr.append(error)
        weight_arr[i, :] = weight.T
        print("迭代 {} 损失：{},weight参数：{}".format(i + 1, error, weight.T.tolist()))

    return weight,loss_arr,weight_arr


if __name__ == '__main__':
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    features, labels = create_sample_set()
    X = np.ones((2, 100))
    X[1] = np.mat(features)
    X = X.T
    Y = labels.reshape(100, 1)
    weights,loss_array,weights_array = gradient_descent(X, Y, learning_rate=0.000001)
    # 绘制曲线
    fig = plt.figure()

    ax1 = fig.add_subplot(2, 2, 1)
    ax1.set_title("样本数据分布" )
    ax1.scatter(features, labels)
    ax2 = fig.add_subplot(2, 2, 2)
    ax2.set_title("梯度下降拟合效果" )
    ax2.scatter(features, labels)
    ax2.plot(features, (X * weights).T.tolist()[0])
    ax3 = fig.add_subplot(2, 2, 3)
    ax3.set_title("随着迭代次数增加loss走势")
    ax3.plot(range(len(loss_array)), loss_array)
    ax4 = fig.add_subplot(2, 2, 4)
    ax4.set_title("随着迭代数增加学习的参数逐渐稳定")
    ax4.plot(np.array(weights_array))


    plt.show()

模型使用的学习率很小，可以尝试加大学习率（会出现问题），这个时候可以考虑对样本数据进行标准化。