矩阵论笔记：奇异值分解SVD(Singular Value Decomposition)以及应用总结！

奇异值分解SVD(Singular Value Decomposition)以及应用总结！

一、相关概念

奇异值分解（Singular Value Decomposition）是线性代数中一种重要的矩阵分解(Matrix Decomposition)，奇异值分解则是特征分解在任意矩阵上的推广。在信号处理、统计学等领域有重要应用。这篇文章主要说下奇异值分解，这个方法在机器学习的一些算法里占有重要地位。

1.1、正交矩阵

如果一个矩阵满足以下几个条件，则此矩阵就是正交矩阵：

• 是一个方阵
• 和自己的转置矩阵的矩阵乘积 $=$ 单位矩阵 $E$，即是：$A{A}^T=A^{T}A=E$ ，其中 $E$ 为单位矩阵。

如果$A$为一个正交矩阵，则A满足以下条件：

• $A$ 的转置矩阵也是正交矩阵
• $A{A}^T=A^{T}A=E$（其中 $E$ 为单位矩阵）
• $A$ 的各行是单位向量且两两正交
• $A$ 的各列是单位向量且两两正交
• $|A|=1$ 或 $-1$
• $A^T=A^{-1}$，$A$ 的转置矩阵等于 $A$ 的逆矩阵

1.2、正定矩阵

如果对于 所有的非零实系数向量 $z$，都有 $z^{T}Az>0$，则称矩阵 $A$ 是正定的。正定矩阵的行列式必然大于 0， 所有特征值也必然大于0。相对应的，半正定矩阵的行列式必然大于等于0。对于 $n$ 阶实对称矩阵 $A$，下列条件是等价的：

• $A$ 是正定矩阵；
• $A$ 的一切顺序主子式均为正；
• $A$ 的一切主子式均为正；
• $A$ 的特征值均为正；
• 存在实可逆矩阵 $C$，使 $A=C^{\prime }C$；
• 存在秩为 $n$ 的 $m\times n$ 实矩阵 $B$，使 $A=B^{\prime }B$；
• 存在主对角线元素全为正的实三角矩阵 $R$，使 $A=R^{\prime }R$

根据正定矩阵的定义及性质，判别对称矩阵 $A$ 的正定性有两种方法：

• 求出 $A$ 的所有特征值。若 $A$ 的特征值均为正数，则 $A$ 是正定的；若 $A$ 的特征值均为负数，则 $A$ 为负定的。
• 计算 $A$ 的各阶顺序主子式。若 $A$ 的各阶顺序主子式均大于零，则 $A$ 是正定的；若 $A$ 的各阶顺序主子式中，奇数阶主子式为负，偶数阶为正，则 $A$ 为负定的。

例： 判断矩阵是否正定

$$Q=\left\{\begin{array}{ccc}6& -3& 1\\ -3& 2& 0\\ 1& 0& 4\end{array}\right\}$$

• 解：对称矩阵 $Q$ 的三个顺序主子式依次为 ：
  $$\begin{array}{c}|6|=6>0\\ \left|\begin{array}{cc}6& -3\\ -3& 2\end{array}\right|=3>0\\ \left|\begin{array}{ccc}6& -3& 0\\ -3& 2& 0\\ 1& 0& 4\end{array}\right|=10>0\end{array}$$
  矩阵 $Q$ 是正定的

二、特征值分解（EVD）

• 实对称矩阵的分解，就是矩阵对角化！
  在理解奇异值分解之前，需要先回顾一下特征值分解，如果矩阵 $A$ 是一个 $m\times m$ 的实对称矩阵（即 $A=A^T$），那么它可以被分解成如下的形式。
  $$A=Q\Sigma Q^T=Q\left[\begin{array}{cccc}{\lambda }_1& \cdots & \cdots & \cdots \\ \cdots & {\lambda }_2& \cdots & \cdots \\ \dots & \dots & \ddots & \dots \\ \cdots & \cdots & \cdots & {\lambda }_m\end{array}\right]Q^T\text{\hspace{1em}(1)}$$
  其中 $Q$ 为标准正交阵，即有 $Q{Q}^T=E$，$\Sigma$ 为对角矩阵( $A$ 的特征值组成的对角矩阵！)，且上面的矩阵的维度均为 $m\times m$。${\lambda }_i$ 称为特征值，$q_i$ 是 $Q$（特征矩阵）中的列向量，称为特征向量。

注意：$E$在这里表示单位阵，式 $(1)$ 的具体求解过程就不多叙述了，可以回忆一下大学时的线性代数。简单地有如下关系：$A{q}_i={\lambda }_i{q}_i,q_i^T{q}_j=1(i\ne j)$。

• 任意矩阵的分解

上面的特征值分解，对矩阵有着较高的要求，它需要被分解的矩阵 $A$ 为实对称矩阵，但是现实中，我们所遇到的问题一般不是实对称矩阵。那么当我们碰到一般性的矩阵，即有一个 $m\times n$ 的矩阵 $A$，它是否能被分解成上面的式 $(1)$ 的形式呢？当然是可以的，这就是我们下面要讨论的内容。

三、奇异值分解（SVD）

3.1、奇异值分解定义

有一个 $m\times n$ 的实数矩阵 $A$，我们想要把它分解成如下的形式
$$A=U\Sigma V^T\text{\hspace{1em}(2)}$$
其中 $U$ 和 $V$ 均为单位正交阵(任意2行互相垂直，长度为1，列也是一样)，即有 $U{U}^T=E$ 和$V{V}^T=E$, $U$ 称为左奇异矩阵，$V$ 称为右奇异矩阵，$\Sigma$ 仅在主对角线上有值，我们称它为奇异值。其它元素均为 $0$。上面矩阵的维度分别为 $U\in R^{m\times m},\Sigma \in R^{m\times n},V\in R^{n\times n}$。一般地$\Sigma$有如下形式：
$$\Sigma ={\left[\begin{array}{ccccc}{\sigma }_1& 0& 0& 0& 0\\ 0& {\sigma }_2& 0& 0& 0\\ 0& 0& \ddots & 0& 0\\ 0& 0& 0& \ddots & 0\end{array}\right]}_{m\times n}$$
其中：${\sigma }_i$ 为奇异值，特征值开根号就是奇异值。

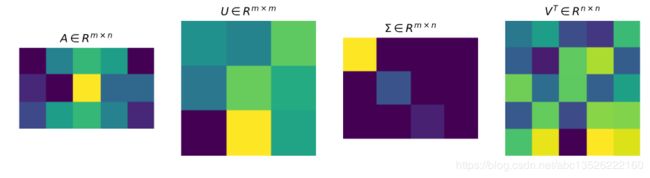
对于奇异值分解，我们可以利用上面的图形象表示，图中方块的颜色表示值的大小，颜色越浅，值越大。对于奇异值矩阵 $\Sigma$，只有其主对角线有奇异值，其余均为 $0$。

3.2、奇异值求解

正常求上面的 $U,V,\Sigma$ 不便于求，我们可以利用如下性质：
$$\begin{array}{rl}A{A}^T& =U\Sigma V^{T}V{\Sigma }^T{U}^T=U\Sigma {\Sigma }^T{U}^T\\ A^{T}A& =V{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^T\Sigma V^T\end{array}\text{\hspace{1em}(3,4)}$$ 这样的话，$A{A}^T$ 和 $A^{T}A$ 都变成了对称矩阵，就可以利用第二部分中的特征值分解，算出特征值，特征向量。

注意：需要指出的是，这里 $\Sigma {\Sigma }^T$ 与 ${\Sigma }^T\Sigma$ 在矩阵的角度上来讲，它们是不相等的，因为它们的维数不同 $\Sigma {\Sigma }^T\in R^{m\times m}$，而 ${\Sigma }^T\Sigma \in R^{n\times n}$，但是它们在主对角线的奇异值是相等的，即有：
$$\Sigma {\Sigma }^T={\left[\begin{array}{cccc}{\sigma }_1^2& 0& 0& 0\\ 0& {\sigma }_2^2& 0& 0\\ 0& 0& \ddots & 0\\ 0& 0& 0& \ddots \end{array}\right]}_{\mathrm{m}\times \mathrm{m}}{\Sigma }^T\Sigma ={\left[\begin{array}{cccc}{\sigma }_1^2& 0& 0& 0\\ 0& {\sigma }_2^2& 0& 0\\ 0& 0& \ddots & 0\\ 0& 0& 0& \ddots \end{array}\right]}_{n\times n}$$
可以看到式 $(3)$ 与式 $(1)$ 的形式非常相同，进一步分析，我们可以发现 $A{A}^T$ 和 $A^{T}A$ 也是对称矩阵，那么可以利用式 $(1)$，做特征值分解。利用式 $(3)$ 特征值分解，得到的特征矩阵即为 $U$；利用式 $(4)$ 特征值分解，得到的特征矩阵即为 $V$；对 $\Sigma {\Sigma }^T$ 或 ${\Sigma }^T\Sigma$ 中的特征值开方，可以得到所有的奇异值。

四、Numpy快速实现奇异值分解

4.1、纯数学例子1：SVD分解4×2分解

假设我们现在有矩阵 $A$，需要对其做奇异值分解，已知：
$$A=\left(\begin{array}{ll}2& 4\\ 1& 3\\ 0& 0\\ 0& 0\end{array}\right)$$
那么可以求出 $A{A}^T$，如下:
$$A{A}^T=\left(\begin{array}{cccc}20& 14& 0& 0\\ 14& 10& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\text{\hspace{1em}(5)}$$
接下来就是求这个矩阵的特征值和特征向量了:
$$\begin{array}{c}A{A}^{T}x=\lambda x\\ \left(A{A}^T-\lambda E\right)x=0\end{array}\text{\hspace{1em}(6)}$$
要想该方程组有非零解（即非零特征值），那么系数矩阵 $A{A}^T-\lambda E$ 的行列式必须为 $0$
$$\left|\begin{array}{cccc}20-\lambda & 14& 0& 0\\ 14& 10-\lambda & 0& 0\\ 0& 0& -\lambda & 0\\ 0& 0& 0& -\lambda \end{array}\right|=0\text{\hspace{1em}(7)}$$
求解这个行列式我就不再赘述了，这个直接使用行列式展开定理就可以了，可以得到 $\lambda 1\approx 29.86606875，\lambda 2\approx 0.13393125，\lambda 3=\lambda 4=0$；有 4 个特征值，因为特征多项式 $|A{A}^T-\lambda E|$是一个 $4$ 次多项式。对应的单位化过的特征向量为
$$\left(\begin{array}{cccc}0.81741556& -0.57604844& 0& 0\\ 0.57604844& 0.81741556& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{\hspace{1em}(8)}$$
这就是矩阵 $U$ 了。 同样的过程求解$A^{T}A$ 的特征值和特征向量，求得 $\lambda 1\approx 0.13393125，\lambda 2\approx 29.86606875$，将特征值降序排列后对应的单位化过的特征向量为:
$$\left(\begin{array}{cc}0.4045358& -0.9145143\\ 0.9145143& 0.40455358\end{array}\right)\text{\hspace{1em}(9)}$$ 这就是矩阵 $V$ 了。 而矩阵 $\Sigma$ 根据上面说的为特征值的平方根构成的对角矩阵(又大到小排序)：
$$\left(\begin{array}{cc}5.4649857& 0\\ 0& 0.36596619\\ 0& 0\\ 0& 0\end{array}\right)\text{\hspace{1em}(10)}$$ 到此，SVD 分解就结束了，原来的矩阵 $A$ 就被分解成了 $3$ 个矩阵的乘积。
$$A_{4\times 2}=U_{4\times 4}{\Sigma }_{4\times 2}{V}_{2\times 2}^T\text{\hspace{1em}(11)}$$ $$\left(\begin{array}{cc}2& 4\\ 1& 3\\ 0& 0\\ 0& 0\end{array}\right)=\left(\begin{array}{cccc}0.81741556& -0.57604844& 0& 0\\ 0.57604844& 0.81741556& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{cc}5.4649857& 0\\ 0& 0.36596619\\ 0& 0\\ 0& 0\end{array}\right){\left(\begin{array}{cc}0.40453358& -0.9145143\\ 0.9145143& 0.40455358\end{array}\right)}^T$$

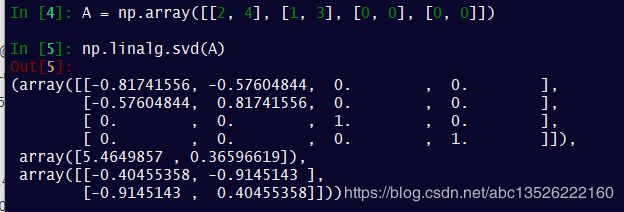
4.2、Numpy 实战4.1

使用pyhon中的numpy包的 linalg.svd() 来求解 SVD。分别对上面做特征值分解，得到如下结果：

4.3、纯数学例子2：SVD分解3×2分解

• 要分解的矩阵 $W$，分解为：$W=U\Sigma V^T$；
  $$W=\left[\begin{array}{ll}1& 1\\ 0& 1\\ 1& 0\end{array}\right]\text{\hspace{1em}(13)}$$

• 首先计算：
  $$C=W^{T}W=\left[\begin{array}{lll}1& 0& 1\\ 1& 1& 0\end{array}\right]\left[\begin{array}{ll}1& 1\\ 0& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{ll}2& 1\\ 1& 2\end{array}\right]\text{\hspace{1em}(14)}$$ 求出 $C$ 的特征值：${\lambda }_1=3,{\lambda }_2=1,{\lambda }_3=0$；特征向量：
  $$v_1=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right],v_2=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}}\end{array}\right]$$

• 其次计算：
  $$B=W{W}^T=\left[\begin{array}{ll}1& 1\\ 0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{lll}1& 0& 1\\ 1& 1& 0\end{array}\right]=\left[\begin{array}{lll}2& 1& 1\\ 1& 1& 0\\ 1& 0& 1\end{array}\right]\text{\hspace{1em}(15)}$$
  求出$B$ 的特征值：${\lambda }_1=3,{\lambda }_2=1,{\lambda }_3=0$，特征向量：
  $$u_1=\left[\begin{array}{c}\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\end{array}\right],u_2=\left[\begin{array}{c}0\\ \frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right],u_3=\left[\begin{array}{c}\frac{-1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}}\end{array}\right]$$

• 最终$W$矩阵可以分解为如下。注意一下公式中的最后一项是转置，只是这里转置之后，仍然和原来相等。奇异值就是特征值开根号(对角线降序排列) $$\left[\begin{array}{ll}1& 1\\ 0& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{ccc}\frac{2}{\sqrt{6}}& 0& -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& \frac{-1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\end{array}\right]\left[\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\end{array}\right]\text{\hspace{1em}(16)}$$ 其中$\sqrt{3}$和 $1$为 $2$ 个奇异值，等于前面求出来的特征值开根号。

• 又等于如下：第1个奇异值，配第1列，配第1行，加上第2个奇异值，配第2列，配第2行。就是看做2个矩阵相加！ $$=\sqrt{3}\left[\begin{array}{c}\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}\\ \frac{\sqrt{6}}{\sqrt{6}}\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]+\left[\begin{array}{c}0\\ -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\end{array}\right]$$

• 就是看做矩阵相加！$$W=U\Sigma V^T=\sqrt{{\lambda }_1}{u}_1{\left(v_1\right)}^T+\sqrt{{\lambda }_2}{u}_2{\left(v_2\right)}^T$$

• 也就是说SVD分解可以把$W$改写成（拆成）这个样子，这就是SVD分解最想做的事情，以这个例子来说，这2个奇异值都是挺大的，但是在通常有一些例子里面，你的矩阵很大，奇异值很多，你的奇异值有些很大，有些很小。如果你把小的奇异值丢掉，但其实整个算出来的数字并不是差的太多，这是一个好处，可以减小计算。我们可以把一些小的奇异值丢掉，分解完我就可以分解成很多奇异值相加，但是我们把小的丢掉，所以这是SVD分解最实用的部分。

• 丢掉小的奇异值有以下2个目的：

1. 减小计算量；
2. 消除杂讯；这个奇异值非常小的情况其实它是在测量上的杂讯造成， 有时候还可以把杂讯消除掉。

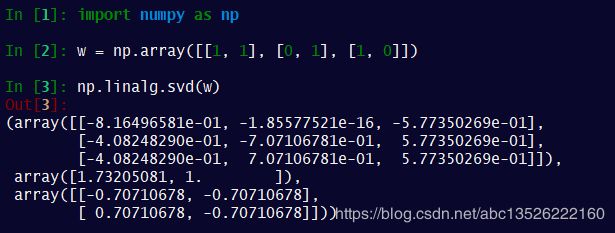
4.4、Numpy 实战4.3

五、SVD分解应用：图像压缩

5.1、分步骤解读

• 在图像压缩中的应用；这里暂时用numpy自带的svd函数做图像压缩。
• ①读取图片

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

# 读取图片
img_eg = mpimg.imread(r"C:\Users\devinzhang\Desktop\timg.jpg")
print(img_eg.shape)

• 打印结果：图片的大小是$526\times 640\times 3$

(526, 640, 3)
Process finished with exit code 0

• ② 奇异值分解：我们先将图片变成【526，640×3】，再做奇异值分解，并且从svd函数中得到的奇异值 $sigma$ 它是从大到小排列的

# 奇异值分解
img_temp = img_eg.reshape(526, 640 * 3)
U, Sigma, VT = np.linalg.svd(img_temp)
print(Sigma)

• ③取前部分奇异值重构图片
  1、如果处理的是一维数组，则得到的是两数组的內积。
  2、如果是二维数组（矩阵）之间的运算，则得到的是矩阵乘法（mastrix product）。
  3、np.diag(Sigma[0:sval_nums])对角矩阵

# 取前60个奇异值
sval_nums = 30
img_restruct1 = (U[:,0:sval_nums]).dot(np.diag(Sigma[0:sval_nums])).dot(VT[0:sval_nums,:])
img_restruct1 = img_restruct1.reshape(526, 640,3)

# 取前120个奇异值
sval_nums = 120
img_restruct2 = (U[:,0:sval_nums]).dot(np.diag(Sigma[0:sval_nums])).dot(VT[0:sval_nums,:])
img_restruct2 = img_restruct2.reshape(526, 640,3)

• ④将图片显示出来看一下，对比下效果

fig, ax = plt.subplots(1,3,figsize = (24,32))

ax[0].imshow(img_eg)
ax[0].set(title = "src")
ax[1].imshow(img_restruct1.astype(np.uint8))
ax[1].set(title = "nums of sigma = 30")
ax[2].imshow(img_restruct2.astype(np.uint8))
ax[2].set(title = "nums of sigma = 120")
plt.show()

5.2、完整代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

# 读取图片
img_eg = mpimg.imread(r"C:\Users\devinzhang\Desktop\timg.jpg")
print(img_eg.shape)

# 奇异值分解
img_temp = img_eg.reshape(526, 640 * 3)
U, Sigma, VT = np.linalg.svd(img_temp)
print(Sigma)

# 取前60个奇异值
sval_nums = 30
img_restruct1 = (U[:,0:sval_nums]).dot(np.diag(Sigma[0:sval_nums])).dot(VT[0:sval_nums,:])
img_restruct1 = img_restruct1.reshape(526, 640,3)

# 取前120个奇异值
sval_nums = 120
img_restruct2 = (U[:,0:sval_nums]).dot(np.diag(Sigma[0:sval_nums])).dot(VT[0:sval_nums,:])
img_restruct2 = img_restruct2.reshape(526, 640,3)


fig, ax = plt.subplots(1,3,figsize = (24,32))

ax[0].imshow(img_eg)
ax[0].set(title = "src")
ax[1].imshow(img_restruct1.astype(np.uint8))
ax[1].set(title = "nums of sigma = 30")
ax[2].imshow(img_restruct2.astype(np.uint8))
ax[2].set(title = "nums of sigma = 120")
plt.show()

参考博客

参考了一下作者的博客，还有一些其它资源，再这里表示感谢！

• https://www.cnblogs.com/endlesscoding/p/10033527.html
• https://blog.csdn.net/u010099080/article/details/68060274
• https://blog.csdn.net/asd136912/article/details/79146151
• https://blog.csdn.net/u012421852/article/details/80475497
• https://www.bilibili.com/video/av15971352/?p=3