深度学习DeepLearning.ai系列课程学习总结：11. 优化算法理论讲解

转载过程中，图片丢失，代码显示错乱。

为了更好的学习内容，请访问原创版本：

http://www.missshi.cn/api/view/blog/5a2272ad9112b35ff3000000

Ps：初次访问由于js文件较大，请耐心等候（8s左右）

在本文中，我们将了解一些机器学习中的优化算法基本理论。

主要包括：

1. Mini-Batch梯度下降法

2. 指数加权平均法

3. 动量梯度下降法

4. RMSProp梯度下降法

5. Adam优化算法

6. 学习速率衰减

7. 局部最优问题

Mini-Batch梯度下降法

深度学习是一个需要不断迭代，不断尝试才能得到一个合适的模型。 
因此，提高训练速度对于整个加快迭代的进度非常重要。 
由于深度学习只有在依赖大数据时，才能发挥出很好的效果；而利用海量的数据进行训练时，往往训练速度会非常慢。

下面我们来了解一下Mini-Batch梯度下降法，它很大的提高了对海量数据的训练速度。 
之前我们学到过，通过对数据进行矢量化运行，可以很好的利用机器的并行计算能力从而提高计算速度。 
但是当训练样本数非常大时，例如500万时。训练速度仍然会非常慢。 
主要的原因是因为目前的硬件设备没有足够的内存可以支持如此大量的数据同时进行计算。 
因此，如果在每次迭代中对全量的数据进行计算的话，对于海量数据时，训练速度仍然会是非常慢的。

那么如何提高训练速度呢？一个可行的方法是对海量数据进行分为若干组。 
每次迭代过程中，对其中的一组数据进行计算并进行迭代。而不再是每次迭代过程中使用全量数据。 
这些每个小组就是我们称的Mini-Batch。

假设每个Mini-Batch中包含1000个样本。 
那么第一次迭代时，我们使用的是第1个到第1000个样本； 
第二次迭代时，我们使用的是第1001个到第2000个样本； 
… 
假设我们一共有500万个样本，每次迭代使用1000个样本进行迭代，那么每次遍历样本需要经历5000次迭代。 
PS：在后续内容中，我们将使用 X{t} X{t}表示第t个Mini-Batch输入样本。 
下面，我们将每次遍历样本（epoch）的基本流程实现过程表示如下：

   
   
   
   

    
    
    
    
for t = 1, ... , 5000 { 
    
    
    
    
    针对x{t}进行前向传播计算：
    
    
    
    
        Z = WX{t} + b
    
    
    
    
        A = g(Z)
    
    
    
    
    计算当前批次的代价函数
    
    
    
    
    反向传播计算出dW和db
    
    
    
    
    更新W和b
    
    
    
    
}
   
   
   
   

整个训练过程中，可能需要经过多次遍历样本（多个epoch）才能达到稳定。

下面，我们通过对比Batch梯度下降法和MiniBatch梯度下降法来更好的理解其原理： 
在使用Batch梯度下降法时，每次迭代的过程中，代价函数总是单调下降的： 
 
而当我们是MiniBatch梯度下降法时，由于每次迭代过程中仅仅是针对一小部分数据进行迭代，所以不能保证每次迭代过程中代价函数都是下降的。但是其整体趋势是不断下降的： 

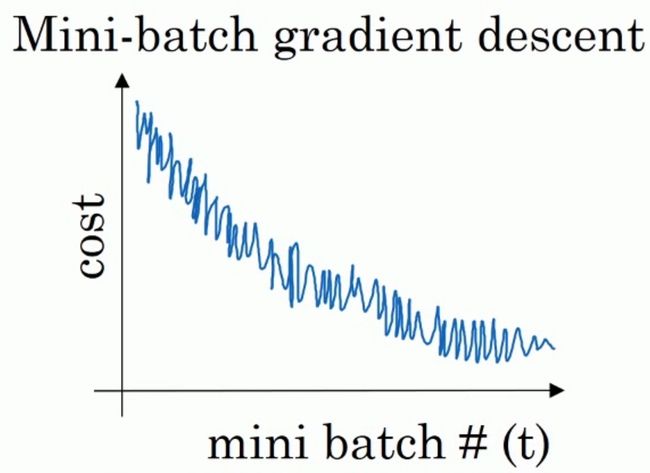
那么，在MiniBatch梯度下降法中，我们需要选择一个超参数batch-size的值。 
首先，我们来考虑两种特殊情况：

• 当batch-size=样本数量m时：该方法实际为Batch梯度下降法。此时，每个Batch为全量的数据集。
• 当batch-size=1时：该方法实际为随机梯度下降法。此时，每个Batch为一个样本。

MiniBatch梯度下降法、随机梯度下降法、Batch梯度下降法三种方法的代价函数逼近图如下所示： 
 
其中，对于Batch梯度下降法而言，其没有发生震荡，稳定逼近最优值，需要的迭代次数最少，但是耗时最多。而对于随机梯度下降法，其波动程度最大，需要的迭代次数最多。而MiniBatch梯度下降法位于两者之间。 
对于随机梯度下降法而言，虽然其计算速度很快，但是它忽略了利用向量化带来的速度提升。而是在每次计算中使用当前样本进行训练。 
MiniBatch梯度下降法很好地结合了随机梯度下降法、Batch梯度下降法：一方面利用了向量化带来的计算效率提升，寻优过程的减少了迭代次数。另一方面，避免了海量数据造成的计算速度慢的问题。

那么batch-size的值究竟应该如何选择呢？

1. 当训练样本集不大时（小于2000），可以直接使用Batch梯度下降法。
2. 其他情况下batch-size通常可以选择64，128, 256， 512。(主要考虑计算机内存/显存的影响)

指数加权平均法

在后续的内容中，我们将会学习一些更加高效的优化算法。 
而作为其基础，我们首先需要学习一个内容：指数加权平均法。 
假设我们拥有了过去180天的伦敦气温，我们需要对后续的每日温度进行预测： 
 
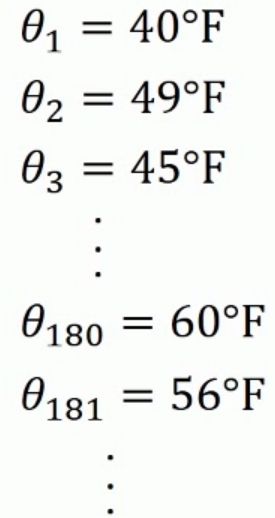
我们将其表示在图像中，得到的结果如下： 
 
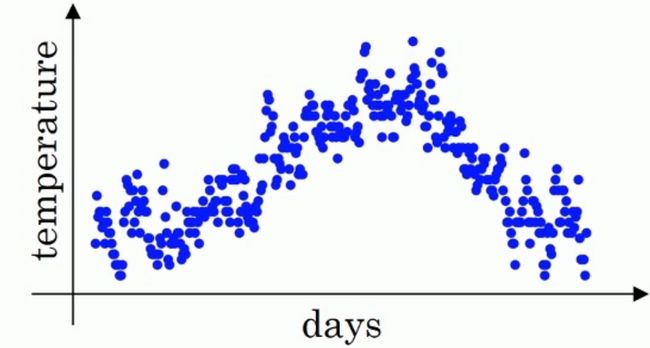
如果我们期望计算温度的趋势的话（局部平均值），我们可以这么做： 

v0=0v1=0.9v0+0.1θ1...vt=0.9vt−1+0.1θt v0=0v1=0.9v0+0.1θ1...vt=0.9vt−1+0.1θt

按照如上方式，我们可以得到如下的折线图： 
 
下面，我们将刚才的公式进行参数化： 

vt=βvt−1+(1−β)θt vt=βvt−1+(1−β)θt

在刚才的假设中，我们设置 β=0.9 β=0.9。 
通常，最终的结果可以近似认为是前 11−β 11−β天的平均数字。 
例如，当 β=0.9 β=0.9时，可以近似认为是过去10天的平均值。 
当 β=0.98 β=0.98时，可以近似认为是过去50天的平均值。 
当 β=0.5 β=0.5时，可以近似认为是过去2天的平均值。 
 
上图显示了当 β β分别取不同值时的预测结果。 
其中，红线表示了 β=0.9 β=0.9时的结果，绿线表示了当 β=0.98 β=0.98时的结果，而黄线表示了当 β=0.5 β=0.5时的结果。可以发现随着 β β值越大曲线越平缓，而当 β β值越小时曲线越陡峭。

接下来，我们了解一下指数加权平均的本质内容。 
首先仍然从如下公式开始入手： 

vt=βvt−1+(1−β)θt vt=βvt−1+(1−β)θt

假设 β=0.9 β=0.9时，那么有： 

v100=0.9v99+0.1θ100v99=0.9v98+0.1θ99... v100=0.9v99+0.1θ100v99=0.9v98+0.1θ99...

此时，将其展开我们可以得到如下结果： 

v100=0.1θ100+0.1∗0.9∗θ99+0.1∗0.92∗θ98+… v100=0.1θ100+0.1∗0.9∗θ99+0.1∗0.92∗θ98+…

这就是加权平均的含义，对之前的数据添加相关的权重。 
那么具体在应用的时候如何实现呢？基本的伪代码如下：

   
   
   
   

    
    
    
    
v = 0
    
    
    
    
for theta in theta_list:
    
    
    
    
    v = beta * v + (1 - beta) * theta
   
   
   
   

从代码中，我们可以看出它有一个很大的优点就是只需要存储一个变量 v v的值即可，而不需要把所有过程中的 v v全部存储下来。

下面，我们要继续学习一个偏差修正的方法，来是的我们计算的平均值更加有效。 
对于细心的同学，可能在之前的内容中所有困惑，当我们在使用如下公式计算时： 

vt=βvt−1+(1−β)θt vt=βvt−1+(1−β)θt

当 θ=0.98 θ=0.98时,  v1 v1应该是从接近于0开始的。然而，我们之前的曲线的起点并不是零。 
那是我们进行了 偏差修正后的结果，真实曲线应该如下图中的紫线所示： 

我们可以看到紫色的曲线起点值很小，这与真实的结果不太符合。 
下面，我们来讲解一下 偏差修正的实现方式： 

vt=vt1−βt vt=vt1−βt

下面，我们以 θ=0.98 θ=0.98， t=2 t=2时进行举例： 

v2=v21−0.982=0.0196θ1+0.02θ20.0396 v2=v21−0.982=0.0196θ1+0.02θ20.0396

momentum梯度下降法

下面我们来学习一种更加高效的优化算法：momentum梯度下降法。 
假设我们期望优化的代价函数图如下，其中，红点位置表示最优值： 

那么通常情况下，我们训练过程中的曲线大致如下： 

可以发现在波动过程中的大量的上下波动影响了寻优的速度，同时制约了我们使用更大的学习速率。 
实际上，我们希望的是在纵轴（无效波动）上减少迭代过程中的波动程度，而在横轴（寻优路径）上加快学习速率。 
那么，此时我们可以利用之前学习到的加权平均法。 
此时，经过加权平均法处理后，在无效波动上，由于会对一段时间的波动取平均值，可以有效的减小过程中的波动程度。 
具体实现的过程基本如下：

   
   
   
   

    
    
    
    
for iter in iterations:
    
    
    
    
    计算每次迭代过程中的dW, db；
    
    
    
    
    利用加权平均计算V_dW：beta * V_dw + (1-beta)dW;
    
    
    
    
    利用加权平均计算V_db: beta * V_db + (1-beta)db;
    
    
    
    
    更新W和b：W=W-alpha*V_dW; b=b-alpha*V_db;
   
   
   
   

Ps：在实践中发现， β=0.9 β=0.9通常是一个比较有效的选值。

RMSProp梯度下降法

RMSProp梯度下降法是另外一个有效的优化算法。 
同样也是利用了指数加权平均法来进行，相比momentum梯度下降法而言，只是从另外一个角度考虑。 
具体实现的过程基本如下：

   
   
   
   

    
    
    
    
for iter in iterations:
    
    
    
    
    计算每次迭代过程中的dW, db；
    
    
    
    
    利用加权平均计算S_dW：beta * S_dw + (1-beta)dW ^ 2;
    
    
    
    
    利用加权平均计算S_db: beta * S_db + (1-beta)db ^ 2;
    
    
    
    
    更新W和b：W=W-alpha*(dW/(S_dW)^0.5); b=b-alpha*(db/(S_db)^0.5);
   
   
   
   

Ps：下面，我们来解释一下上述方法的原理： 
我们的目标是减少无效波动，而在无效波动的方向上变化速率通常更大。 
因此，我们将dW和db除以变化的波动速度可以有效的降低无效波动的程度。

Adam优化算法

Adam优化算法是目前应用最广泛的优化算法之一。 
它是将momentum梯度下降法和RMSProp梯度下降法结合得到的。 
具体的实现如下：

   
   
   
   

    
    
    
    
for iter in iterations:
    
    
    
    
    计算每次迭代过程中的dW, db；
    
    
    
    
    利用加权平均计算V_dW：beta1 * V_dw + (1-beta1)dW;
    
    
    
    
    利用加权平均计算V_db: beta1 * V_db + (1-beta1)db;
    
    
    
    
    利用加权平均计算S_dW：beta2 * S_dw + (1-beta2)dW ^ 2;
    
    
    
    
    利用加权平均计算S_db: beta2 * S_db + (1-beta2)db ^ 2;
    
    
    
    
    # 偏差修正
    
    
    
    
    V_dW_correct = V_dW/(1-beta1^iter)
    
    
    
    
    V_db_correct = V_db/(1-beta1^iter)
    
    
    
    
    S_dW_correct = S_dW/(1-beta2^iter)
    
    
    
    
    S_db_correct = S_db/(1-beta2^iter)
    
    
    
    
    # 更新W和b：
    
    
    
    
    W=W-alpha*(V_dW_correct/(S_dW_correct)^0.5 + epsilon); b=b-alpha*(V_db_correct/(S_db_correct)^0.5 + epsilon);
   
   
   
   

在这个过程中，涉及到了如下一些超参数：

1. alpha(需要调试)
2. beta1(通常可以设置为0.9)
3. beta2(通常可以设置为0.999)
4. epsilon(通常可以设置为 10−8 10−8)

学习速率衰减

加快学习过程的一个方法是随着时间的推移，慢慢降低学习速率，我们称之为学习速率衰减。 
那么为什么学习速率衰减会有助于加快学习过程呢？ 
以下图为例： 

在上图中，蓝色的线表示使用固定学习速率得到的结果。可以发现当它已经在最优点附近值，由于学习速率较大，还呈现出较大的波动。 
而为了减小其在最优值附近的波动，我们需要设置更小的学习速率，而这个过程则会减慢学习的过程。 
绿线表示了学习速率衰减时的情况，在早期时，保持较大的学习速率加速向最优值逼近。而当其达到最优值附近时，则学习速率不断降低从而导致较小的波动程度。 
我们常用的学习速率衰减方法如下： 

α=11+decay_rate∗epoch_num∗α0 α=11+decay_rate∗epoch_num∗α0

其中，epoch_num表示第一轮数据集遍历。 
当我们假设 α0=0.2 α0=0.2， decay_rate=1 decay_rate=1时：

Epoch	appha
1	0.1
2	0.67
3	0.5
4	0.4

除此之外，还有一些其他常用的学习速率衰减方法，例如： 

α=0.95epoch_num∗α0α=kepoch_num0.5∗α0α=离散函数方法等 α=0.95epoch_num∗α0α=kepoch_num0.5∗α0α=离散函数方法等

此外，有时我们在进行长时间训练时，还可以手动进行学习速率衰减。

局部最优问题

在早期的机器学习过程中，寻优过程中陷入局部最优往往是研究者需要努力解决的问题。 
我们将在本节中简单的讲解局部最优的概念以及目前在深度学习中局部最优的影响。 
在谈到局部最优时，我们脑中往往会浮现出类似的图形： 
 
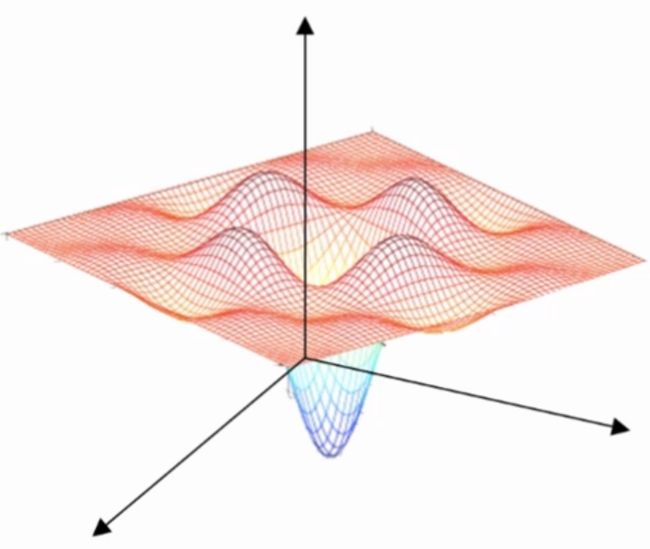
在该图中，存在着很多的局部最优点，而如果针对该模型应用梯度下降法时，我们很容易的陷入局部最优中。 
这种印象造成了我们认为局部最优对于我们的优化过程有着很大的影响。 
然而在深度学习中，由于参数的维度很大，局部最优其实对本身的寻优过程影响并不大。 
因为在实际应用中，我们所达到的梯度为0的点通常并不是最不最优点，而是鞍点，例如下图所示： 
 
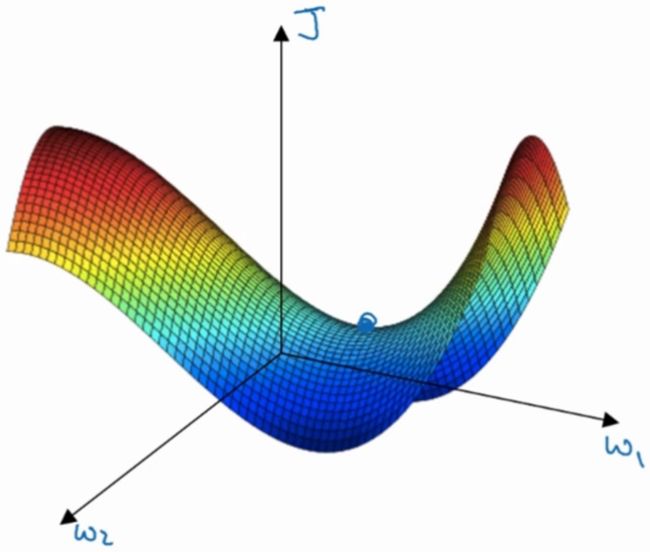
而对于鞍点而言，其实并没有达到局部最优，梯度下降法仍然后继续进行寻优迭代过程。 
假设在一个20000维的空间中，如果想要达到局部最优点，那么就需要所有的维度方向全部达到局部最优值，这种概率往往是非常小的，可以忽略不计。

更多更详细的内容，请访问原创网站：

http://www.missshi.cn/api/view/blog/5a2272ad9112b35ff3000000

Ps：初次访问由于js文件较大，请耐心等候（8s左右）