OpenSSL:基于RSA算法的签名和验证(原理+代码)
数字签名和验证(Digital signature and verification)
- 数字签名主要用于验证被签数据在传输过程中是否被篡改
- 包含加密算法(encryption)和摘要算法(digest)
- 摘要算法包括MD族和SHA族,特点是变长输入,定长输出,输出即为目标数据的摘要
- 加密使用RSA非对称算法,包括公钥和私钥,私钥对消息(Message)进行加密,公钥对数据和签名进行解密
使用OpenSSL进行RSA签名和验证
生成简单的数据文件,私钥和公钥
# Create a file containing all lower case alphabets
$ echo abcdefghijklmnopqrstuvwxyz > myfile.txt
# Generate 512 bit Private key
$ openssl genrsa -out myprivate.pem 512
# Separate the public part from the Private key file.
$ openssl rsa -in myprivate.pem -pubout > mypublic.pem
# Cat the contents of private key
$ cat myprivate.pem
-----BEGIN RSA PRIVATE KEY-----
MIIBOwIBAAJBAMv7Reawnxr0DfYN3IZbb5ih/XJGeLWDv7WuhTlie//c2TDXw/mW
914VFyoBfxQxAezSj8YpuADiTwqDZl13wKMCAwEAAQJAYaTrFT8/KpvhgwOnqPlk
NmB0/psVdW6X+tSMGag3S4cFid3nLkN384N6tZ+na1VWNkLy32Ndpxo6pQq4NSAb
YQIhAPNlJsV+Snpg+JftgviV5+jOKY03bx29GsZF+umN6hD/AiEA1ouXAO2mVGRk
BuoGXe3o/d5AOXj41vTB8D6IUGu8bF0CIQC6zah7LRmGYYSKPk0l8w+hmxFDBAex
IGE7SZxwwm2iCwIhAInnDbe2CbyjDrx2/oKvopxTmDqY7HHWvzX6K8pthZ6tAiAw
w+DJoSx81QQpD8gY/BXjovadVtVROALaFFvdmN64sw==
-----END RSA PRIVATE KEY-----利用OpenSSL签名
- 摘要算法:SHA1
- 填充(Padding)标准:PCKS#1 v1.5(默认)
# Sign the file using sha1 digest and PKCS1 padding scheme
$ openssl dgst -sha1 -sign myprivate.pem -out sha1.sign myfile.txt
# Dump the signature file
$ hexdump sha1.sign
0000000 91 39 be 98 f1 6c f5 3d 22 da 63 cb 55 9b b0 6a
0000010 93 33 8d a6 a3 44 e2 8a 42 85 c2 da 33 fa cb 70
0000020 80 d2 6e 7a 09 48 37 79 a0 16 ee bc 20 76 02 fc
0000030 3f 90 49 2c 2f 2f b8 14 3f 0f e3 0f d8 55 59 3d0000040利用OpenSSL验证
# Verify the signature of file
$ openssl dgst -sha1 -verify mypublic.pem -signature sha1.sign myfile.txt
Verified OK签名和验证原理
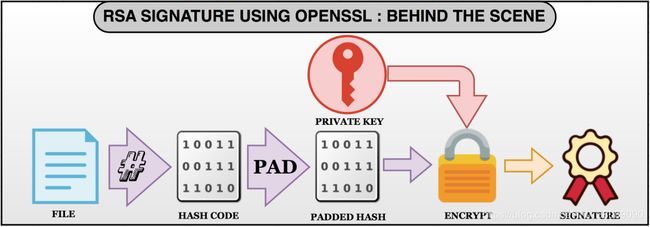
签名的生成
Step1:生成摘要
- 利用hash算法生成消息的摘要,SHA1会生成160bit(20字节)的hash值
- 另外OpenSSL还支持SHA224, SHA256, SHA384, SHA512, MD4, MD5等算法
$ sha1sum myfile.txt
8c723a0fa70b111017b4a6f06afe1c0dbcec14e3 myfile.txtStep2:填充hash值
- 填充值加在生成的hash值之前,openssl中默认是PKCS1
- PKCS#1 v1.5的填充策略是:00||01||PS||00||T||Hash
- 其中,T是不同填充策略的标识符(每种策略都有自己的MAGIC BYTES),PS是FF字符
- 填充后的摘要长度等于消息长度
$ PADDING=0001ffffffffffffffffffffffffffffffffffffffffffffffffffff00
$ ANS1_SHA1_MAGIC=3021300906052b0e03021a05000414
$ SHA1_HASH=`sha1sum myfile.txt | cut -d ' ' -f1`
$ echo $PADDING$ANS1_SHA1_MAGIC$SHA1_HASH
0001ffffffffffffffffffffffffffffffffffffffffffffffffffff003021300906052b0e03021a050004148c723a0fa70b111017b4a6f06afe1c0dbcec14e3Step3:从私钥中提取RSA算法的模(modulus)和私钥指数
其格式如下:
$ openssl rsa -in myprivate.pem -text -noout
Private-Key: (512 bit)
modulus:
00:cb:fb:45:e6:b0:9f:1a:f4:0d:f6:0d:dc:86:5b:
6f:98:a1:fd:72:46:78:b5:83:bf:b5:ae:85:39:62:
7b:ff:dc:d9:30:d7:c3:f9:96:f7:5e:15:17:2a:01:
7f:14:31:01:ec:d2:8f:c6:29:b8:00:e2:4f:0a:83:
66:5d:77:c0:a3
publicExponent: 65537 (0x10001)
privateExponent:
61:a4:eb:15:3f:3f:2a:9b:e1:83:03:a7:a8:f9:64:
36:60:74:fe:9b:15:75:6e:97:fa:d4:8c:19:a8:37:
4b:87:05:89:dd:e7:2e:43:77:f3:83:7a:b5:9f:a7:
6b:55:56:36:42:f2:df:63:5d:a7:1a:3a:a5:0a:b8:
35:20:1b:61
prime1:
00:f3:65:26:c5:7e:4a:7a:60:f8:97:ed:82:f8:95:
e7:e8:ce:29:8d:37:6f:1d:bd:1a:c6:45:fa:e9:8d:
ea:10:ff
prime2:
00:d6:8b:97:00:ed:a6:54:64:64:06:ea:06:5d:ed:
e8:fd:de:40:39:78:f8:d6:f4:c1:f0:3e:88:50:6b:
bc:6c:5d
exponent1:
00:ba:cd:a8:7b:2d:19:86:61:84:8a:3e:4d:25:f3:
0f:a1:9b:11:43:04:07:b1:20:61:3b:49:9c:70:c2:
6d:a2:0b
exponent2:
00:89:e7:0d:b7:b6:09:bc:a3:0e:bc:76:fe:82:af:
a2:9c:53:98:3a:98:ec:71:d6:bf:35:fa:2b:ca:6d:
85:9e:ad
coefficient:
30:c3:e0:c9:a1:2c:7c:d5:04:29:0f:c8:18:fc:15:
e3:a2:f6:9d:56:d5:51:38:02:da:14:5b:dd:98:de:
b8:b3重新编码打印出私钥的模和指数:
# Store the output of private key info in a variable
$ PRKEY_INFO=`openssl rsa -in myprivate.pem -text -noout`
# Grep and format string to output Modulus
$ MODULUS=`echo "$PRKEY_INFO" | grep modulus: -A 5 | tail -5`
$ echo `echo $MODULUS | tr -cd [:alnum:]`
00cbfb45e6b09f1af40df60ddc865b6f98a1fd724678b583bfb5ae8539627bffdcd930d7c3f996f75e15172a017f143101ecd28fc629b800e24f0a83665d77c0a3
# Grep and format string to output privateExponent
$ PREXP=`echo "$PRKEY_INFO" | grep privateExponent: -A 5 | tail -5`
$ echo `echo $PREXP | tr -cd [:alnum:]`
61a4eb153f3f2a9be18303a7a8f964366074fe9b15756e97fad48c19a8374b870589dde72e4377f3837ab59fa76b55563642f2df635da71a3aa50ab835201b61Step4:利用私钥中的模和指数对padding的hash值进行签名
# Signing is done in python which supports big number arithmetic
# Convert padded hash (calculated in step 2) to integer
[python]$ padded_hash = int('0001ffffffffffffffffffffffffffffffffffffffffffffffffffff003021300906052b0e03021a050004148c723a0fa70b111017b4a6f06afe1c0dbcec14e3', 16)
# Convert modulus (calculated in step 3) to integer
[python]$ modulus = int('00cbfb45e6b09f1af40df60ddc865b6f98a1fd724678b583bfb5ae8539627bffdcd930d7c3f996f75e15172a017f143101ecd28fc629b800e24f0a83665d77c0a3', 16)
# Convert private exponent (calculated in step 3) to integer
[python]$ private_exp = int('61a4eb153f3f2a9be18303a7a8f964366074fe9b15756e97fad48c19a8374b870589dde72e4377f3837ab59fa76b55563642f2df635da71a3aa50ab835201b61', 16)
# Sign the message: (padded_hash ** private_exp) % modulus
# (a**b)%c is efficiently caluclated by pow(a, b, c)
[python]$ sign = hex(pow(padded_hash, private_exp, modulus))[2:]
# Format and the signature
[python]$ slist = list(sign)
[python]$ for i in range(len(sign) - 2, 0, -2) : slist.insert(i,' ')
[python]$ slist[len(slist) - 48 : 0 : -48] = ['\n']*(len(slist)//48)
[python]$ print("".join(slist))
91 39 be 98 f1 6c f5 3d 22 da 63 cb 55 9b b0 6a
93 33 8d a6 a3 44 e2 8a 42 85 c2 da 33 fa cb 70
80 d2 6e 7a 09 48 37 79 a0 16 ee bc 20 76 02 fc
3f 90 49 2c 2f 2f b8 14 3f 0f e3 0f d8 55 59 3d数据签名完成!
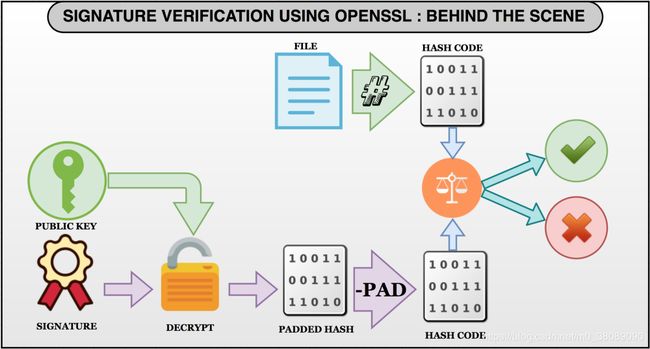
验证签名
step1:从公钥中获取模和指数
其中,公钥中包含:模、指数以及公钥大小,公钥指数一般设置为65537(0x10001)
# Get modulus and public exponent from public key
$ openssl rsa -pubin -inform PEM -text -noout < mypublic.pem
Public-Key: (512 bit)
Modulus:
00:cb:fb:45:e6:b0:9f:1a:f4:0d:f6:0d:dc:86:5b:
6f:98:a1:fd:72:46:78:b5:83:bf:b5:ae:85:39:62:
7b:ff:dc:d9:30:d7:c3:f9:96:f7:5e:15:17:2a:01:
7f:14:31:01:ec:d2:8f:c6:29:b8:00:e2:4f:0a:83:
66:5d:77:c0:a3
Exponent: 65537 (0x10001)重新编码后打印:
# Store the output of public key info in a variable$ PBKEY_INFO=`openssl rsa -pubin -inform PEM -text -noout < mypublic.pem`
# Grep and format string to output Modulus
$ MODULUS=`echo "$PBKEY_INFO" | grep Modulus: -A 5 | tail -5`
$ echo `echo $MODULUS | tr -cd [:alnum:]`
00cbfb45e6b09f1af40df60ddc865b6f98a1fd724678b583bfb5ae8539627bffdcd930d7c3f996f75e15172a017f143101ecd28fc629b800e24f0a83665d77c0a3
# Grep to print public exponent
$ echo "$PBKEY_INFO" | grep Exponent:
Exponent: 65537 (0x10001)step2:转换并打印签名
签名一般是二进制文件,需要转换成大数进行运算
# sha1.sign is the signature file sent along with data file.
$ echo `hexdump sha1.sign | cut -c 9- | tr -cd [:alnum:]`
9139be98f16cf53d22da63cb559bb06a93338da6a344e28a4285c2da33facb7080d26e7a09483779a016eebc207602fc3f90492c2f2fb8143f0fe30fd855593dstep3:对签名进行解密
# Convert signature file to integer (Obtained in step 2)[python]$ signature = int('9139be98f16cf53d22da63cb559bb06a93338da6a344e28a4285c2da33facb7080d26e7a09483779a016eebc207602fc3f90492c2f2fb8143f0fe30fd855593d', 16)
# Convert modulus to integer (Obtained in step 1)
[python]$ modulus = int('00cbfb45e6b09f1af40df60ddc865b6f98a1fd724678b583bfb5ae8539627bffdcd930d7c3f996f75e15172a017f143101ecd28fc629b800e24f0a83665d77c0a3', 16)
# Set the public_exp
[python]$ public_exp = 65537
# Convert sign to hash: (sign ** public_exp) % modulus
# (a**b)%c is efficiently caluclated by pow(a, b, c)
[python]$ padded_hash = hex(pow(signature, public_exp, modulus))
[python]$ padded_hash
'0x1ffffffffffffffffffffffffffffffffffffffffffffffffffff003021300906052b0e03021a050004148c723a0fa70b111017b4a6f06afe1c0dbcec14e3'step4:移除padding获得消息的hash值
# Remove the padded hash to slice the hash of message
[python]$ padded_hash[-40:]
'8c723a0fa70b111017b4a6f06afe1c0dbcec14e3'可以看到验签获得的hash值与消息的digest值完全一致,验签成功!
一句话总结:
数据的签名就是利用rsa对消息的摘要进行加密的结果,验签就是再对数据计算摘要,然后与签名解密结果进行比较,如果一致,则验签成功。
原文链接:https://medium.com/@bn121rajesh/rsa-sign-and-verify-using-openssl-behind-the-scene-bf3cac0aade2 (science online)