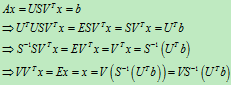The solution of Ax=b
Mldivide is a matlab function, which is also denoted as"\". It solve systems of linear equations Ax = B for x. The method is called left divide.
![]() , The A-1 is on the left of b, this is the reason called left divide. But the A-1 exists only when A is a square matrix. When A is not a square matrix, we must apply SVD method to solve this equation. This is how "\" works in matlab.
, The A-1 is on the left of b, this is the reason called left divide. But the A-1 exists only when A is a square matrix. When A is not a square matrix, we must apply SVD method to solve this equation. This is how "\" works in matlab.
![]()
![]()
[m,n] = size(U); U is a column orthogonal matrix
[n,n] = size(s); S is a diagonal matrix
[n,n] = size(V); V is an orthogonal matrix
U is a column orthogonal matrix, which means the multiplication of the same column is 1, while the multiplication of different columns is, just likes the following equation:
![]()
E is the unit matrix, whose size is n-by-n.
So, we can deduct:
S is a diagonal matrix, so S-1 is diagonal as well. Each diagonal element of S-1 is the multiplicative inverse number of the corresponding diagonal element of S.
![]()
E is the unit matrix, whose size is n-by-n.
So, we can continue deduct:
The size of UTb is n-by-1. We have to stick to the right order of computing.
V is an orthogonal matrix, so
We can get:
VS-1 can be calculated first, since both of them are square matrixs.
The solution of ![]() is
is ![]() .
.