dnn文本分类

简介

文本分类任务根据给定一条文本的内容，判断该文本所属的类别，是自然语言处理领域的一项重要的基础任务。具体的，本任务是对文本quey进行分类，任务流程如下：

1. 收集用户query数据。
2. 清洗，标记。
3. 模型设计。
4. 模型学习效果评估。

运行

训练： sh ＋x train.sh

预测： python infer.py

输入／输出

输入样本：

label text（分词后）

0 龙脉温泉 住宿 1 龙马 机场 飞机 2 龙里 旅游 其中，label 0，1和2分别代表：酒店，票务和住宿。

预估样本：

2 0.0002 0.0001 0.9997 港澳 7 日 自助游 label prob text 其中，label为概率最大的类别，即2旅游，中间三个数值为每个类别的概率。

DNN 模型

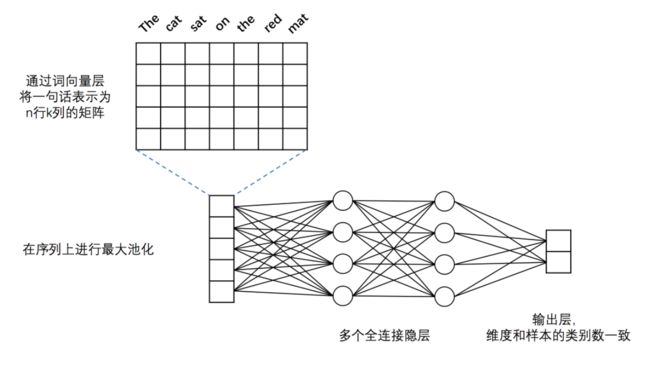
DNN 模型结构入下图所示：

 

图1. 本例中的 DNN 文本分类模型

在 PaddlePaddle 实现该 DNN 结构的代码见 network_conf.py 中的 fc_net 函数，模型主要分为如下几个部分：

• 词向量层：为了更好地表示不同词之间语义上的关系，首先将词语转化为固定维度的向量。训练完成后，词与词语义上的相似程度可以用它们的词向量之间的距离来表示，语义上越相似，距离越近。关于词向量的更多信息请参考PaddleBook中的词向量一节。
• 最大池化层：最大池化在时间序列上进行，池化过程消除了不同语料样本在单词数量多少上的差异，并提炼出词向量中每一下标位置上的最大值。经过池化后，词向量层输出的向量序列被转化为一条固定维度的向量。例如，假设最大池化前向量的序列为[[2,3,5],[7,3,6],[1,4,0]]，则最大池化的结果为：[7,4,6]。
• 全连接隐层：经过最大池化后的向量被送入两个连续的隐层，隐层之间为全连接结构。
• 输出层：输出层的神经元数量和样本的类别数一致，例如在二分类问题中，输出层会有2个神经元。通过Softmax激活函数，输出结果是一个归一化的概率分布，和为1，因此第$i$个神经元的输出就可以认为是样本属于第$i$类的预测概率。

　　该 DNN 模型默认对输入的语料进行二分类（class_dim=3），embedding（词向量）维度默认为28（emd_dim=28），两个隐层均使用Tanh激活函数（act=paddle.activation.Tanh()）。需要注意的是，该模型的输入数据为整数序列，而不是原始的单词序列。事实上，为了处理方便，我们一般会事先将单词根据词频顺序进行 id 化，即将词语转化成在字典中的序号。

源码：

import sys
import math
import gzip

from paddle.v2.layer import parse_network
import paddle.v2 as paddle

__all__ = ["fc_net", "convolution_net"]


def fc_net(dict_dim,
           class_num,
           emb_dim=28,
           hidden_layer_sizes=[28, 8],
           is_infer=False):
    """
    define the topology of the dnn network
    :param dict_dim: size of word dictionary
    :type input_dim: int
    :params class_num: number of instance class
    :type class_num: int
    :params emb_dim: embedding vector dimension
    :type emb_dim: int
    """

    # define the input layers
    data = paddle.layer.data("word",
                             paddle.data_type.integer_value_sequence(dict_dim))
    if not is_infer:
        lbl = paddle.layer.data("label",
                                paddle.data_type.integer_value(class_num))

    # define the embedding layer
    emb = paddle.layer.embedding(input=data, size=emb_dim)
    # max pooling to reduce the input sequence into a vector (non-sequence)
    seq_pool = paddle.layer.pooling(
        input=emb, pooling_type=paddle.pooling.Max())

    for idx, hidden_size in enumerate(hidden_layer_sizes):
        hidden_init_std = 1.0 / math.sqrt(hidden_size)
        hidden = paddle.layer.fc(
            input=hidden if idx else seq_pool,
            size=hidden_size,
            act=paddle.activation.Tanh(),
            param_attr=paddle.attr.Param(initial_std=hidden_init_std))

    prob = paddle.layer.fc(
        input=hidden,
        size=class_num,
        act=paddle.activation.Softmax(),
        param_attr=paddle.attr.Param(initial_std=1.0 / math.sqrt(class_num)))

    if is_infer:
        return prob
    else:
        return paddle.layer.classification_cost(
            input=prob, label=lbl), prob, lbl


def convolution_net(dict_dim,
                    class_dim=2,
                    emb_dim=28,
                    hid_dim=128,
                    is_infer=False):
    """
    cnn network definition
    :param dict_dim: size of word dictionary
    :type input_dim: int
    :params class_dim: number of instance class
    :type class_dim: int
    :params emb_dim: embedding vector dimension
    :type emb_dim: int
    :params hid_dim: number of same size convolution kernels
    :type hid_dim: int
    """

    # input layers
    data = paddle.layer.data("word",
                             paddle.data_type.integer_value_sequence(dict_dim))
    lbl = paddle.layer.data("label", paddle.data_type.integer_value(class_dim))

    # embedding layer
    emb = paddle.layer.embedding(input=data, size=emb_dim)

    # convolution layers with max pooling
    conv_3 = paddle.networks.sequence_conv_pool(
        input=emb, context_len=3, hidden_size=hid_dim)
    conv_4 = paddle.networks.sequence_conv_pool(
        input=emb, context_len=4, hidden_size=hid_dim)

    # fc and output layer
    prob = paddle.layer.fc(
        input=[conv_3, conv_4], size=class_dim, act=paddle.activation.Softmax())

    if is_infer:
        return prob
    else:
        cost = paddle.layer.classification_cost(input=prob, label=lbl)

return cost, prob, lbl

 

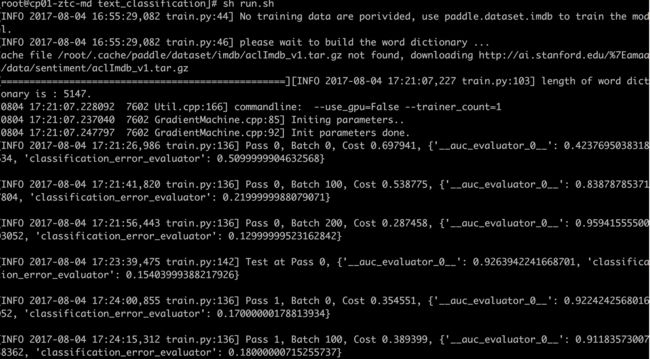
训练结果如下图：

预估结果：

 

转载于:https://www.cnblogs.com/rongyux/p/7295571.html