软件设计师复习03

1.1.4校验码

　　1.校验码用来检测传送的数据是否出错。

　　2.将数据出现的编码分为两类：合法编码：用于传输数据

　　　　　　　　　　　　　　　　错误编码：不允许在数据中出现的编码

　　3.奇偶校验码：是一种通过增加冗余位使得码字中"1"的个数恒为奇数或偶数的编码方法,它是一种检错码。

                                在实际使用时又可分为垂直奇偶校验、水平奇偶校验和水平垂直奇偶校验等几种。

拓展：1.垂直奇偶校验

垂直奇偶校验又称为纵向奇偶校验,它是将要发送的整个信息块分为定长p位的若干段(比如说q段),每段后面按"1"的个数为奇数或偶数的规律加上一位奇偶位,如图2.19所示。问位信息(I11,I21,…,Ipl,I12,…,Ipq)中,每p位构成一段(即图中的一列),共有q段(即共有q列〉。每段加上一位奇偶校验冗余位,即图中的rio编码规则为

  

注意:此间的"+"指的是模二加,也即异或运算。

      图中箭头给出了串行发送的顺序,即逐位先后次序为I11,I21,…,Ip1,r1,I12,…,Ipa,r2,…,儿,…,I间,rq。在编码和校验过程中,用硬件方法或软件方法很容易实现上述连续半加运算,而且可以边发送边产生冗余位;同样,在接收端也可边接收边进行校验后去掉校验位。

     垂直奇偶校验方法的编码效率为R=p/(p+1)。通常,取一个字符的代码为一个信息段,这种垂直奇偶校验有时也称为字符奇偶校验。例如,在8位字符代码(即用8位二进制数位表示一个字符)中,p=8,编码效率便为8/9。

垂直奇偶校验方法能检测出每列中的所有奇数位错,但检测不出偶数位的错。对于突发错误来说,奇数位错与偶数位错的发生概率接近于相等,因而对差错的漏检率接近于1/2。

         2.水平奇偶校验

     为了降低对突发错误的漏检率,可以采用水平奇偶校验方法。水平奇偶校验又称为横向奇偶校验,它是对各个信息段的相应位横向进行编码,产生一个奇偶校验冗余位,如图2.20所示,编码规则为

    若每个信息段就是一个字符的话,这里的q就是发送的信息块中的字符数。

    水平奇偶校验的编码效率为R=q/(q+1)。

     水平奇偶校验不但可以检测出各段同一位上的奇数位错,而且还能检测出突发长度≦p的所有突发错误，因为按发送顺序从图2.20中可见，突发长度≦p的突发错误必然分布在不同的行中，且每行一位，所以可以检查出差错，他的漏检率比垂直奇偶校验方法低。但是实现水平奇偶校验码时，不论是采用硬件还是软件方法，都不能在发送过程中产生奇偶校验冗余位边插入发送,而必须等待要发送的全部信息块到齐后,才能计算冗余位,也就是一定.要使用数据缓冲器,因此它的编码和检测实现起来都要复杂一些。

　　3.水平垂直奇偶校验

       同时进行水平奇偶校验和垂直奇偶校验就构成水平垂直奇偶校验,也称为纵横奇偶校实验,如图2.21所示。若水平垂直都采用偶校验,则水平垂直奇偶校验的编码效率为R=pq/[(p+1)(q+1)]。.

     水平垂直奇偶校验能检测出所有3位或3位以下的错误(因为此时至少在某一行或某一'列上有一位错)、奇数位错、突发长度<=p+1的突发错以及很大一部分偶数位错。测量表.明,这种方式的编码可使误码率降至原误码率的百分之一到万分之一。

    水平垂直奇偶校验不仅可检错,还可用来纠正部分差错。例如数据块中仅存在1位错'时,便能确定错码的位置就在某行和某列的交叉处,从而可以纠正它

　　4.海明码：

　　　海明码是一种可以纠正一位差错的编码。它是利用在信息位为k位，增加r位冗余位，构成一个n=k+r位的码字，然后用r个监督关系式产生的r个校正因子来区分无错和在码字中的n个不同位置的一位错。它必需满足以下关系式： 2r ≥ k+r+1 或 2r ≥ n+1 海明码的编码效率为： R=k/(k+r) 式中 k为信息位位数 r为增加冗余位位数。

          编码步骤 　　(1)根据信息位数，确定校验位数，2^r >= k+r+1，其中，k为信息位数，r为校验位数。求出满足不等式的最小r，即为校验位数。 　　

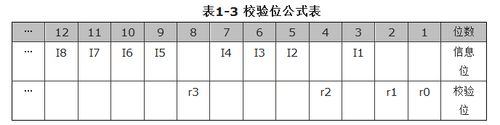
　　　　　　　　　 (2)计算机校验位公式。

                                     

                                表1-3其实可以当成一个公式来套用，如有已经编码的数据 1100 1001 0111。我们只需把这些数据填充到校验公式，即可得到信息位与校验位。

                                填充的方法是这样的，首先看数据的最低位(即右边第1位)，最低位为1，把1填充在公式表的r0位置，接着取出数据的次低位数据(即右边第2位)，

                                把它填充到r1位置，把右边第3位数填充到I1位置。依此类推，我们可以得到表1-4。

　　　　　　　　　　

　　　　　　　　　　   表中第2行数据为1100 001 1，这就是数据1100 1001 0111的编码信息，而表格第3行是1 011，这便是校验位。 　　

　　　　　　　　 注意： n 校验位rn 所在位数为2^n，其余由信息位填充; n 信息位下标从1开始，而校验位下标从0开始。 　　

　　　　　　　　 例如：I8 对应的第十二位12=2^3+2^2，I7对应的第十一位11=2^3+2^1+2^0，I6 对应的第十位10=2^3+2^1，I5 对应的第九位9=2^3+2^0，

                                一直写到I1对应的第三位。 　　

                                校验位rn 由前面位数写成2的幂之和中包含2^n 的位数对应的信息位之和构成 　　

　　　　　　　　　　　　　 例如： r3=I8+I7+I6+I5    （+表示异或） 　　

　　　　　　　　(3)求校验位。根据上面我们所说的计算公式可以求出校验位。 　　

　　　　　　　　(4)求海明码。根据上面的表格填充后，写出海明码。

　　5.循环冗余校验码（CRC）：是数据通信领域中最常用的一种差错校验码，其特征是信息字段和校验字段的长度可以任意选定。

　　　（1）生成CRC码的基本原理：任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。例如：代码1010111对应的多项式为x⁶+x⁴+x²+x+1，而多项式为x⁵+x³+x²+x+1对应的代码101111。

         （2）CRC码集选择的原则：若设码字长度为N，信息字段为K位，校验字段为R位(N=K+R)，则对于CRC码集中的任一码字，存在且仅存在一个R次多项式g(x)，使得

V(x)=A(x)g(x)=x^Rm(x)+r(x);

             其中:    m(x)为K次信息多项式， r(x)为R-1次校验多项式，g(x)称为生成多项式：

                        g(x)=g₀+g₁x+g₂x²+...+g_(R-1)x^(R-1)+g_Rx^R

发送方通过指定的g(x)产生CRC码字，接收方则通过该g(x)来验证收到的CRC码字。

        （3）CRC校验码软件生成方法：借助于多项式除法，其余数为校验字段。

 （海明码部分引用网易博客上的数据及表格）

 

转载于:https://www.cnblogs.com/nuanningan-292684880/archive/2013/02/02/2890382.html