Percolation System

小记：

此为普林斯顿大学在Coursera上开的算法课的第一周编程作业，主要是用Union-Find（并查集）来仿真渗透系统（Percolation System）

主要内容是写两个class：第一个class用来设计渗透系统，添加和描述系统的状态(open, isOpen, isFull, percolate)，难点主要在open方法的的设计，要考虑backwash的问题，还有一个就是将二维坐标映射到一维数组（并查集）中。第二个class用来进行蒙特卡洛模拟，估计出渗透系统的阈值（threshold），需要用到置信区间，具体见链接.

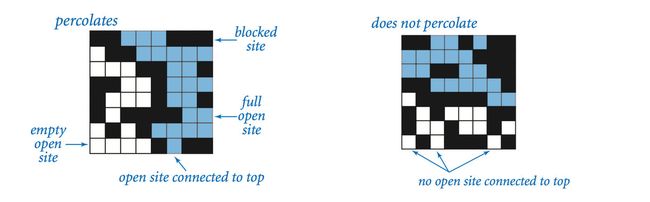
Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.

The model. We model a percolation system using an n-by-n grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)

The problem. In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right).

以上关于项目的部分描述引自官方(具体请点击链接)

---

以下为本人代码（已加注释）96/100 仅供参考

Percolation.java

import edu.princeton.cs.algs4.WeightedQuickUnionUF;

public class Percolation {
    private final WeightedQuickUnionUF uf;
    private final WeightedQuickUnionUF ufBackwash; // 防止反冲
    private boolean[] openArr; // new一个标记节点是否open的数组
    private final int n; // size
    private int openNum = 0; // 记录open节点数
    private final int TOP; // 虚拟top site
    private final int BOTTOM; // 虚拟bottom site

    // 坐标转换 2d -> 1d
    private int xyTo1D(int i, int j){
        return (i - 1) * n + j - 1;
    }

    // 验证有效坐标
    private void validIndex(int i, int j) {
        if (i < 1 || i > n) {
            throw new IllegalArgumentException();
        }
        if (j < 1 || j > n) {
            throw new IllegalArgumentException();
        }

    }

    // 构造器 creates n-by-n grid, with all sites initially blocked
    public Percolation(int n) {
        if (n <= 0) {
            throw new IllegalArgumentException();
        }
        this.n = n;
        this.TOP = n * n; // 虚拟top 并查集中的index
        this.BOTTOM = n * n + 1; // 虚拟bottom 并查集中的index
        // 最后两个为 virtual top/bottom site
        uf = new WeightedQuickUnionUF(BOTTOM + 1);
        // 用于backwash
        ufBackwash = new WeightedQuickUnionUF(BOTTOM + 1);
        // 初始化openArr 初始状态的节点都是closed
        openArr = new boolean[n * n];
        for (int i = 0; i < openArr.length; i++) {
            openArr[i] = false;
        }
    }

    // opens the site (row, col) if it is not open already
    public void open(int row, int col) {
        validIndex(row, col);
        int index = xyTo1D(row, col);
        // 先检查之前是否open，防止重复
        if (!openArr[index]) {
            openArr[index] = true;
            openNum++;
            // 四个方向
            // 不是第一行并且它上面的点已经open了，就连接
            if (row != 1 && openArr[n * (row - 2) + col - 1]) {
                uf.union(index, n * (row - 2) + col - 1);
                ufBackwash.union(index, n * (row - 2) + col - 1);
            }
            // 不是第一列并且它左边的点已经open了，就连接
            if (col != 1 && openArr[n * (row - 1) + col - 2]) {
                uf.union(index, n * (row - 1) + col - 2);
                ufBackwash.union(index, n * (row - 1) + col - 2);
            }
            // 不是最后一行并且它下面的节点已经open了，就连接
            if (row < n && openArr[n * row + col - 1]) {
                uf.union(index, n * row + col - 1);
                ufBackwash.union(index, n * row + col - 1);
            }
            // 不是最后一列并且它右边的节点已经open了，就连接
            if (col < n && openArr[n * (row - 1) + col]) {
                uf.union(index, n * (row - 1) + col);
                ufBackwash.union(index, n * (row - 1) + col);
            }

            if (row == 1) {
                // 第一行节点与虚拟top连接
                uf.union(index, TOP);
                ufBackwash.union(index, TOP);
            }

            if (row == n) {
                // 这里是关键 因为backwash并查集没有虚拟bottom，故不用union
                uf.union(BOTTOM, index);
            }
        }
    }

    // is the site (row, col) open?
    public boolean isOpen(int i, int j) {
        validIndex(i, j);
        return openArr[xyTo1D(i, j)];
    }

    // is the site (row, col) full?
    public boolean isFull(int row, int col) {
        validIndex(row, col);
        // isFull必须首先满足isOpen，同时去backwash并查集去找，因为该并查集不包含bottom site，不会产生反冲
        return openArr[xyTo1D(row, col)] && (ufBackwash.find(xyTo1D(row, col)) == ufBackwash.find(TOP));
    }

    // does the system percolate?
    public boolean percolates() {
        // 检查虚拟top和虚拟bottom是否有相同的root即可
        return (uf.find(TOP) == uf.find(BOTTOM));
    }

    // returns the number of open sites
    public int numberOfOpenSites() {
        return this.openNum;
    }
}

PercolationStats.java

import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdRandom;
import edu.princeton.cs.algs4.StdStats;

public class PercolationStats {
    private final double CONFIDENCE = 1.96;
    //trial times
    private int trial_num;
    //threshold
    private double[] thresholds;

    // perform independent trials on an n-by-n grid
    public PercolationStats(int n,int trials) {
        if (n <= 0 || trials <= 0) {
            throw new IllegalArgumentException();
        }
        trial_num = trials;
        thresholds = new double[trials];
        for (int i = 0; i < trials; i++) {
            Percolation p = new Percolation(n);
            while(!p.percolates()) {
                int row = StdRandom.uniform(n) + 1;
                int col = StdRandom.uniform(n) + 1;
                p.open(row, col);
                if (p.percolates()) break;
            }
            thresholds[i] = (double)p.numberOfOpenSites() / (n * n);
        }
    }

    // sample mean of percolation threshold
    public double mean() {
        return StdStats.mean(thresholds);
    }

    // sample standard deviation of percolation threshold
    public double stddev() {
        return StdStats.stddev(thresholds);
    }

    // low endpoint of 95% confidence interval
    public double confidenceLo() {
        return mean() - CONFIDENCE * stddev() / Math.sqrt(trial_num);
    }

    // high endpoint of 95% confidence interval
    public double confidenceHi() {
        return mean() + CONFIDENCE * stddev() / Math.sqrt(trial_num);
    }

    // test client (see below)
    public static void main(String[] args) {
        int n = 20;
        int trial_num = 1000;
        PercolationStats perc = new PercolationStats(n,trial_num);
        StdOut.println("mean() = "+ perc.mean());
        StdOut.println("stddev() = " + perc.stddev());
        StdOut.println("95% confidence interval = [" + perc.confidenceLo() + ", " + perc.confidenceHi() + "]");
    }
}

---