一、模型的常微分方程及初值
二、ode45求解函数
function r=hudie3(t,x)
global a;
global b;
global c;
a=8/3;b=10;c=28;
r=zeros(3,1);
r(1)=-a*x(1)+x(2)*x(3);
r(2)=-b*x(2)+b*x(3);
r(3)=-x(1)*x(2)+c*x(2)-x(3);
end
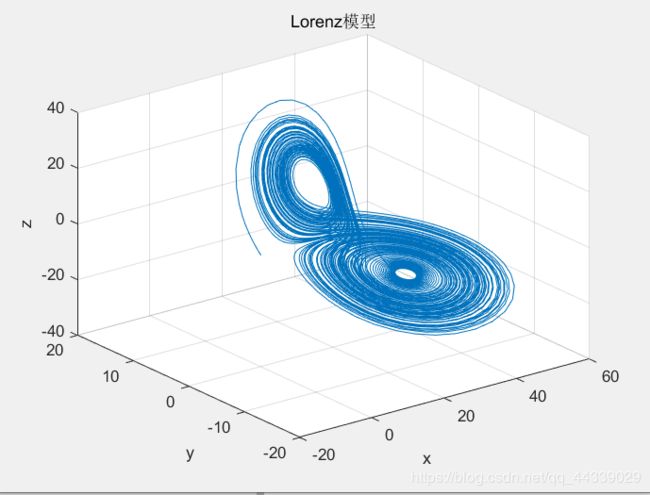
三、绘制混沌系统三维曲线图
a=8/3;b=10;c=28;
t0=[0,100];f0=[0,0,1e-10];
[t,x]=ode45('hudie3',t0,f0);
plot3(x(:,1),x(:,2),x(:,3));
title('Lorenz模型');xlabel('x');ylabel('y');zlabel('z');
grid on
四、绘制混沌系统三个平面上的投影图
a=8/3;b=10;c=28;
t0=[0,100];
f0=[0,0,1e-10];
[t,x]=ode45('hudie3',t0,f0);
subplot(2,2,1)
plot3(x(:,1),x(:,2),x(:,3));
title('Lorenz模型');xlabel('x');ylabel('y');zlabel('z');
grid on
subplot(2,2,2)
plot(x(:,1),x(:,2));
title('Lorenz模型X-Y平面图');xlabel('x');ylabel('y');
grid on
subplot(2,2,3)
plot(x(:,1),x(:,3));
title('Lorenz模型X-Z平面图');xlabel('x');ylabel('z');
grid on
subplot(2,2,4)
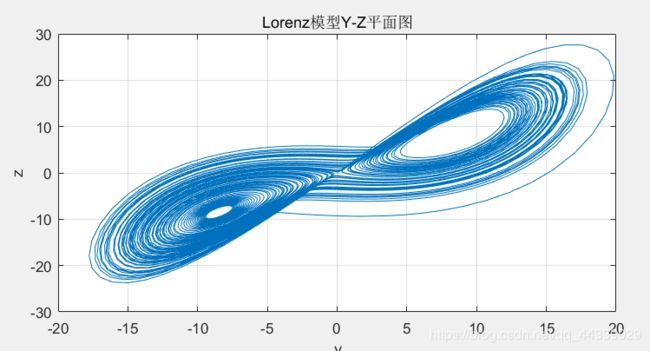
plot(x(:,2),x(:,3));
title('Lorenz模型Y-Z平面图');xlabel('y');ylabel('z');
grid on
五、修改初值观察混沌系统图像的变化
以下是给出的几组任意的初值:
其图像如下:
六、探究各初值对图像的影响的参考代码
a=8/3;b=10;c=28;
for k=0:50:400
t0=[0,100];f0=[k,0,1e-10];
[t,x]=ode45('hudie3',t0,f0);
subplot(3,3,(k+50)/50)
plot3(x(:,1),x(:,2),x(:,3));
title('Lorenz模型');xlabel('x');ylabel('y');zlabel('z');
grid on
end
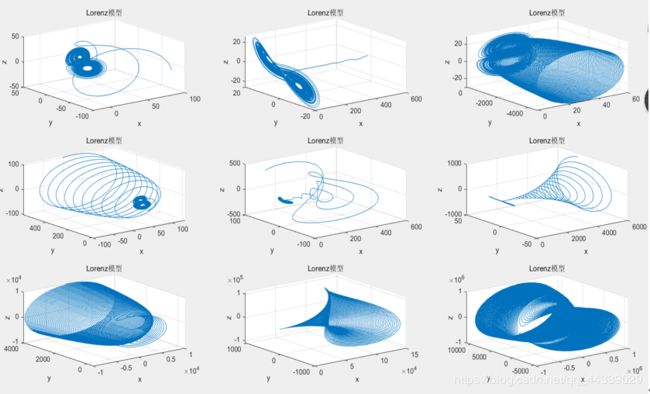
上面程序的图像如下:
探究第一个初值的变化对图像的影响的时候将变量K放在f0向量的第一个参数上,如上程序所示,探究第二个初值的变化对图像的影响的时候将变量K放在f0向量的第二个参数上,以此类推。
参数的取值范围通过修改 for k=0:50:400语句实现,但是注意在修改该语句时对应的 subplot(3,3,(k+50)/50)语句中(k+50)/50也要修改,比如将for k=0:50:400改为for k=0:500:4000,则subplot(3,3,(k+50)/50)应该相应的改为subplot(3,3,(k+500)/500)