线段树新手向攻略

一直想写点什么对读者有用的东西。

上篇说了从基础算法好好学起，那就从线段树开始吧。

 (转帖请注明http://blog.csdn.net/asdfgh0308/article/details/42455529)

一、入坑

线段树，是一种数据结构。大多有用的数据结构，就是通过一定的维护开销，来获得查询、修改等操作开销的降低。

a.它好用吗？在ACM竞赛中还是挺有用的，小比赛到大比赛，简答题到复杂题，都有线段树的身影。嗯，还有人这样评价搞ACM的新人：会写线段树。就是说这个人算是入门了！这样一个能标志着入门ACM的算法，还是要好好学的吧。不过线段树还是有丰富的内涵，不是每个“会写”线段树的人都能又好又快地把线段树应用到实际题目里。

b.它的功能：简单来说，给你一个有序数列/数组，线段树能提供快速的区间操作（例如区间加/减/乘；区间求和/平均/最大最小；区间打标记/染色/记录信息；取第x个还活着的），但不能增、减线段上的元素个数，改变元素的顺序（splay干的活）。

c.它的结构：

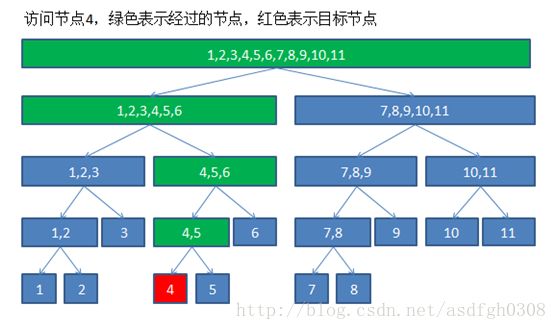
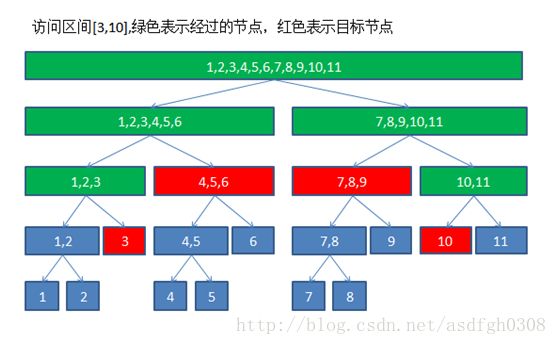
先看示意图：以11个点为例

它是一个完全二叉树，也就是说每个节点左右子树的高度相差不超过1，有右子树必然有左子树。这保证了它的高度是O(logN)。简单证明一下，线段树第一层有1个节点，第二层有2个节点，第x层有2^x-1个节点，2^(x-1-1)

（这里插一句，对于新手，理解logN是一个重要的过程。对于N=100000，默认以2为底，logN只有17，这是一个很小的数字，几乎接近于一个可以忽略的常数了，所以O(N*N)的复杂度到O(N*logN)是一个巨大的优化。即使不是以2为底，只要是对数级别，都可以用换底公式lg x/lg2，这是一个定值，所以底数的变化只是常数变化。）

d.它的实现：结合代码来看一些功能的实现。

网上充斥着各类的线段树实现版本，有些很不好理解，有些甚至直接就有严重bug，我就简要介绍一下我认为比较容易理解的版本。我的线段树写法应该是最傻的那种，十分容易理解的，先贴个基本代码：

#define N 200100
//所需的宏定义，位运算来代替p*2,p*2+1,更高效,宏定义打起来更简短更清晰
#define ls (p<<1)
#define rs (p<<1|1)
#define mid(p) (t[p].l+t[p].r>>1)

//数据结构
struct segmentTree{
    int l,r,v;
    int tag;
}t[N*4];

//懒操作
void lazy(int p){
    if (t[p].tag){
        t[ls].tag=t[rs].tag=t[p].tag;
        t[ls].v=t[rs].v=t[p].tag;
        t[p].tag=0;
    }
}
//回溯更新函数
void update(int p){
    t[p].ma=max(t[ls].ma,t[rs].ma);
}

//建树
void build(int l,int r,int p){
    t[p].l=l;t[p].r=r;t[p].tag=0;
    if (t[p].l==t[p].r){
        t[p].v=v[l];
        return;
    }
    int m=mid(p);
    build(l,m,ls);
    build(m+1,r,rs);
    update(p);
}
//单点访问
void workOnPoint(int pos,int p,int newValue){
    if (t[p].l==t[p].r){
        t[p].v=newValue;
        return;
    }
    lazy(p);
    int m=mid(p);
    if (pos<=m) {
        workOnPoint(pos,ls,newValue);
    }
    else {
        workOnPoint(pos,rs,newValue);
    }
    update(p);
}
//区间操作
int workOnSegment(int l,int r,int p,int newValue){
    if (l==t[p].l&&r==t[p].r){
        t[p].v=newValue;
        return;
    }
    lazy(p);
    int m=mid(p);
    if (r<=m) {
        workOnSegment(l,r,ls,newValue);
    }
    else if (l>m){
        workOnSegment(l,r,rs,newValue);
    }
    else {
        merge(workOnSegment(l,m,ls,newValue),workOnSegment(m+1,r,rs,newValue));
        //merge指将两个部分合并的方法，如果是取最大值就是max，求和就是相加
    }
    update(p);
}

基础结构：结构体segmentTree保存一个节点的参数，包含这个节点的左右区间、节点的值、节点的子树和等等。节点连接关系通过编号来计算，左子树是p*2，右子树是p*2+1，也就是宏定义中的ls，rs。

建树：把数组建立为树状的结构，并统计一些有意义的值（区间和之类）。过程就是把数组平均劈成两段，递归建立子树。O(N)的复杂度。调用的时候注意根是1号节点，build(1,n,1)。

单点访问（修改，标记，查询数组某一个元素）：而我们只知道根是1号节点，这时只要通过根一层一层爬到要的节点就行。爬的过程也很简单，如果这个点在左子树，就往左边爬，否则往右边。示意图如下：

这样爬的层数是O(logN)，复杂度就是O(logN)。对比一下普通的数组，我们只需要知道访问元素的编号就可以通过一次找到这个元素，O(1)。线段树好像更差，别急，看下面。

区间操作（求和、最大值等）。这个时候需要在每个节点上记录一个区间总值。根据区间的范围，我们还是通过1号根节点一层一层地爬来统计，这里爬的方式有所不同，分为三种：1)当目标区间在当前节点的中点之前r<=m，则只需要访问左子树。

2)如果目标区间在中点之后l>=m+1,则只需要访问右子树。

3)否则既要访问左子树又要访问右子树。

看图：

在我推荐的线段树实现里，只要递归的起始目标区间在节点区间内，那么递归过程中就不会出现目标区间不在当前节点区间内的情况（也就是说l>=t[p].l且r<=t[p].r）。注意这里每层不只有一个爬的操作，而是每层有最多会有常数个（4个）。找到在范围内的区间就把区间和加到结果里去。每层有两次，层数是O(logN)，这样复杂度还是O(4*logN)=O(logN)。相比于数组的遍历操作(最差O(N))，线段树就高效得多。

区间操作（加、乘、标记等）。每个点需要一个标记tag。这里还需要用到一个懒操作（lazy）的思想。就是说每次并不把操作做到节点上，而是只做到最上层的被包含的节点。由于访问是自上而下的，当访问到那些没有被修改的节点时，就把懒标记下传，并做操作。这样做操作的层数是logN，每层最多只有常数个操作，复杂度O(logN)。同样，数组实现也要O(N)，这就是线段树优势所在。

一个表对比线段树和数组的效率：

对比项	数组	线段树
空间复杂度	O(N)	O(N)
建立（初始化）	O(N)	O(N)
单点访问	O(1)	O(logN)
区间访问	O(N)	O(logN)

其实线段树并不一定就比数组高效，当单点访问足够多的时候。但是ACM竞赛往往需要考虑的是最差情况，对于N次操作，每次都是整个区间的修改，数组最差情况是O(N*N)，线段树就是O(NlogN)。

e.实现易错点：对于新手，其实这个代码还是比较长的，手打可能会有各种错误。其实我打也各种出错各种浪费时间调试：（，以下都是鲜血淋漓的教训。

1.节点数。

一般是N*4，因为节点编号是通过父节点编号乘2或者乘2加1，乘4比较安全。记得线段树的空间复杂度是O(N)的。

2.区间操作和单点操作递归终止条件的区别。

函数参数里的l、r是实际操作的区间，t[p].l、t[p].r是当前节点表示的区间。

区间操作：if (l==t[p].l&&r==t[p].r) return;

单点操作：if (t[p].l==t[p].r)  return;

很多人写着写着就混了！然后就复杂度退化了！然后就TLE到死了以为线段树做不了这题了！

其实单点操作也可以写成和区间操作一样，这样就不会混了。也就是把所有单点操作改成区间长度为1的情况。workOnPoint(pos,1)==workOnSegment(pos,pos,1)。

3.懒操作(lazy)的实现。

我认为最好的方式还是标记到已做操作的一层。也就是说如果某一个节点上有懒标记，这个节点已经被做过操作，但它的下层节点还没被做操作。

当访问完这层开始访问下层之前，就要将标记下传，并对下层做好操作。这样实现懒标记的意义在于，每次你访问到某个节点，这个节点的值都是正确的。

4.update和return。

有些操作，在询问的时候同时需要修改。而修改时常常需要回溯向上修改，通常是用一个函数update()实现。但是这个函数又需要返回值。可能就变成了这样：

int query(int l,int r,int p){
    if (l==t[p].l&&r==t[p].r)  return t[p].sum;
    int m=mid(p);
    if (r<=m) {
        return query(l,r,ls);
    }
    else if (l>m){
        return query(l,r,rs);
    }
    else {
        return query(l,m,ls)+query(m+1,r,rs);
    }
    update(p);
}

然后又傻了不知道wa在哪儿了。

应该这样写，保证每次update被实际执行：

int query(int l,int r,int p){
    if (l==t[p].l&&r==t[p].r)  return t[p].sum;
    int m=mid(p),ret;
    if (r<=m) {
        ret=query(l,r,ls);
    }
    else if (l>m){
        ret=query(l,r,rs);
    }
    else {
        ret=query(l,m,ls)+query(m+1,r,rs);
    }
    update(p);
    return ret;
}

5.宏定义的惹的祸

有时候为了减少一些函数调用的时间开销这样写：

#define max(a,b) ((a)>(b)?(a):(b))

int query(int l,int r,int p){
    if (l==t[p].l&&r==t[p].r)  return t[p].v;
    int m=mid(p);
    if (r<=m){
        return query(l,r,ls);
    }
    else if (l>m){
        return query(l,r,rs);
    }
    else {
        return max(query(l,m,ls),query(m+1,r,rs));
    }
}

然后又TLE了！又不知道咋整了！

注意宏定义是直接替换，也就是用一个query函数替换a。这样一次max就需要调用两次query。这可不是两倍！每次query都是递归的过程，第一层变成2倍，第二层就是4倍……然后复杂度就变了！所以这种地方还是老老实实用函数写吧。

好啦，基础知识已经讲完了。

f.来切点基础题：

1.hdu1754。求一段区间的最大值，修改某个点的值。改点查段，无需lazy操作就可以实现。代码点这里。

2.poj3264。求区间的最大值最小值之差。没有修改，拿线段树当RMQ用了。代码点这里。

3.poj2528。区间修改，查点。点的范围比较大，还需要离散化一下。代码点这里。

(未完待续)