基于Matlab的对RSA加密算法的一个验证

| 作者原创，转载请注明出处 https://blog.csdn.net/hzberg/article/details/78689643

简介

博主最近有一个讨论课要找点东西讲，浏览网页的时候恰巧看到了RSA算法的博客，介绍得很详细，感兴趣的朋友可以前去阅读：

RSA算法原理

看了这篇博客才知道RSA算法原来是最重要的不对称加密算法之一，也很有趣，于是打算选这个题目。加上曾经有一点基础的数论知识，对相关的内容也不陌生。RSA算法成功的保障在于，对于一个由两个大素数p，q乘积得到的大整数n=pq，将其进行因式分解是很困难的。（最简单的方法在$\sqrt{n}$的数量级）

为了便于说明，还是要简单介绍几个数论里面的概念，这些在任何一本初等数论的书里面应该都有比较完整的介绍：
**互质：**两正整数a，b的最大公约数为1，记作gcd(a,b)=1；
**同余：**给定一个正整数m，如果两个正整数a，b满足（a-b）能够被m整除，则称数a和数b对模m同余，记作$a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}n)$；
**欧拉函数φ(n)：**小于等于n的整数中，与n互质的整数的个数。对素数p来说，显然φ（p）= p - 1；
**模反元素：**对于整数a，b，m，如果 $ab\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则称a，b互为关于m的模反元素；
*欧几里得辗转相除法：主要解决已知两整数a，b求它们最大公约数 gcd(a,b) 的问题；
*扩展欧几里得算法：已知两整数 a，b，用辗转相除法求它们最大公约数 gcd(a,b) ，并根据辗转相除法中的式子，求不定方程 ax+by=gcd(a,b) 的整数解 x，y。

关于上面两种算法的问题和一般实现的思路，可以参照博文

扩展欧几里得算法

有了这些知识的铺垫，我们就可以说明主题了——

RSA加密的步骤

RSA加密中有两个关键要素–用于加密的公钥和用于解密的私钥。以下是公钥和私钥产生的过程：

1、选择两个不同的素数p，q并求其乘积 n=pq。
2、计算欧拉函数φ(n)，这里根据数论的知识（参见简介中的引文1），φ(n)=φ( p )φ(q)=(p-1)(q-1)。
3、选取一个正整数e，要求 1 < e < φ(n) 且e与φ(n)互质。这也就产生了公钥（n，e）。
4、求e关于φ(n)的模反元素d，即求得一个正整数d，满足 $ab\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}\phi )(n)$。

这里前面3个步骤都是易于理解和实现的。步骤4中求解模反元素的问题，实质上等价于求不定方程 ax+by=gcd(a,b) 的一组解 x, y，且其中一个元素为正整数。（这里令a=φ(n)，b=e，且 gcd(e,φ(n))=1 ，需要得到一组整数解 x，y 且 y>0）
于是应用到了扩展欧几里得算法。为了能够验证RSA算法，就需要对扩展欧几里得算法进行实现。第2篇引文中是用递归的方法做的，很简洁。但是对于这种验证性的小例子来说，没有递归的必要，鉴于Matlab已经内置了一些诸如求余、乘方等的数学函数，这里选择用Matlab实现RSA加密算法验证。下面是实现扩展欧几里得算法的.m文件源码：

%Euclid(a,b)接收两个参数,分别是不定方程ax+by=gcd(a,b)中的a和b,且a>b
function Euclid(a,b)
step=0; %辗转相除法的步骤数
i=1; %i是用来记录除数与被除数的数对的下标
pp=[];qq=[]; %创建空数组,记录除数和被除数
if(abs(a)>abs(b))
    p=abs(a);q=abs(b);
else
    q=abs(a);p=abs(b); %这种情形实际不允许,为与数表对应,要求正整数a>b
    pp(i)=p;qq(i)=q;
end
r=mod(p,q);
while r~=0
    i=i+1;
    step=step+1;
    p=q;q=r;r=mod(p,q); %更新下一次辗转相除法要处理的除数和被除数
    pp(i)=p;qq(i)=q; %在数组中记录辗转相除法每一步骤的结果
end %终止状态:q=gcd,r=0
    
x=1;y=0;k=step+1;
%根据辗转相除法记录下来的结果,逆向求一组整数解
while k~=0
    temp=x;
    x=y;
    y=temp-fix(pp(k)/qq(k))*y; %fix,取整函数
    k=k-1;
end
while(x>0) %求得不定方程ax+by=1的整数解,若x>0则y<0.通过调整使得x<0,则y>0
    x=x-b;
end
y=-(x*a-q)/b; %这样就得到了所需要的正整数
fprintf('%d %d\n',x,y)

例如，我们可以试一下求e=23关于φ(n)=120 (120=(11-1)*(13-1)) 的模反元素：

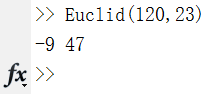
[120×(-9)+23×47=1]

接下来具体看一下RSA加密算法的加密与解密过程：

5、明文信息与数字的对应：这一步骤与常规的编码没有差别，常见的符号系统有ASCII码等，得到数字形式的明文m；
6、通过公钥 (n,e) 得到密文c，加密的形式为：$m^e\equiv c(\mathrm{m}\mathrm{o}\mathrm{d}n)$;
7、使用私钥 (n,d) 解密得数字形式的明文m，解密的依据是：$c^d\equiv m(\mathrm{m}\mathrm{o}\mathrm{d}n)$。关于这一点，实际上可以通过数论的知识证明。可以参照引文1，这里博主简单整理了一下，对于有基本数论知识的读者应该不会困难：


8、最后一步就是把数字明文与文本明文对应了，这是容易做到的。

说了这么多，下面就用一个实际的例子来对照：

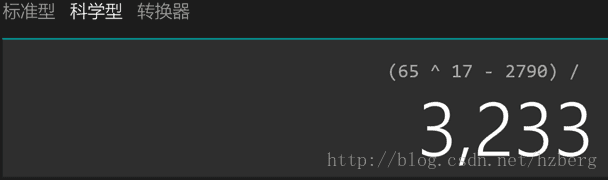
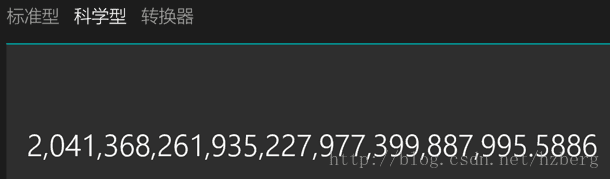
这里需要注明一点，尽管Matlab的计算能力很强大，但是由于RSA算法中往往涉及到很大指数的乘方运算，Matlab中的普通整数类型很容易发生溢出，导致结果错误，下面是一个例子：
$65^{17}\equiv 2790(\mathrm{m}\mathrm{o}\mathrm{d}3233)$
但是Matlab计算出来的结果，余数是887：

这个问题刚开始也困扰了博主很久，但后来有一次用win8.1自带的计算器验证后，发现Matlab是错的……

解决的方法其实是用了Matlab的一个扩展工具箱，全称是 Varible Precision Integer Arithmetic，能够给出大整数计算的准确结果。VPI工具箱可以在Mathworks的官网上下载到，其调用格式例如：

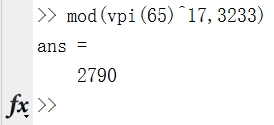
博主水平所限，如有错误，还请读者不吝指正。