浅谈矩阵变换——Matrix
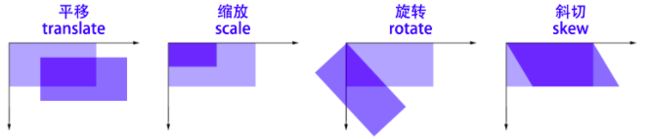
矩阵变换在图形学上经常用到。基本的常用矩阵变换操作包括平移、缩放、旋转、斜切。
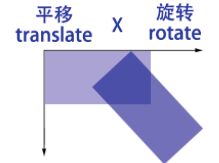
每种变换都对应一个变换矩阵,通过矩阵乘法,可以把多个变换矩阵相乘得到复合变换矩阵。
矩阵乘法不支持交换律,因此不同的变换顺序得到的变换矩阵也是不相同的。
事实上,图像处理时,矩阵的运算是从右边往左边方向进行运算的。这就形成了越在右边(右乘)的矩阵,越先运算(先乘),反之亦然。所以,右乘就是先乘,左乘就是后乘。
复合变换矩阵T = 变换矩阵T1 x 变换矩阵T2 x 变换矩阵T3。
图形是由一个个点组成的,得到变换矩阵T后,左乘以变换前的图形像素矩阵M,即可达到变换后像素矩阵M’,即M' = T x M。
在Android中,用Matrix这个类代表矩阵。Matrix是一个3x3的矩阵,
Matrix提供了基本的变换,translate、scale、rotate、skew,针对每种变换,Android提供了set、pre和post三种操作方式。
- set用于设置单位矩阵中的值。我们通过new Matrix()得到的是一个单位矩阵,后续的矩阵变换都是针对这个单位矩阵进行变换。如Matrix.setRotate(90)、Matrix.setTranslate(10,20)等。
- pre指先乘,相当于矩阵运算中的右乘。如Matrix.setRotate(90),表示M' = M * R(90)。
- post指后乘,相当于矩阵运算中的左乘,如Matrix.setRotate(90),表示M' = R(90) * M。
matrix.setRotate(θ);
matrix.preTranslate(-10, -10); // 先乘
matrix.postTranslate(10, 10); // 后乘点(x0,y0)经过矩阵变换后得到(x,y),如果对图形中的所有点应用该变换矩阵,则产生的效果就是整个图都变换了。那么如何理解上面的变换呢?它是先平移(10,10)还是先平移(-10,-10)?
首先我们得明白上面变换的效果是什么——让图形围绕点(10,10)顺时针旋转角度θ。
按照我们上面说的,实际运算时,是从右边往左开始运算,那么这时的变换顺序是,T(-10,-10)->R(θ)->T(10,10),
把所有的顶点(坐标)位置平移(-10,-10),也就是分别沿x轴y轴的负方向平移10个单位,然后沿着原点(0,0)把顶点旋转角度θ,最后再把顶点的位置平移(10,10).
可见这里变换的是坐标(也就是顶点)位置,坐标系不变。
Android自定义view时,往往在onDraw(canvas)方法里实现绘图,canvas表示画布,我们可以在代码里对画布进行矩阵变换,如下面的代码,
canvas.translate(10, 10);
canvas.rotate(θ);
canvas.translate(-10, -10);效果也是让画布围绕点(10,10)旋转θ度。我们在看看Canvas中translate()方法的注释。
/**
* Preconcat the current matrix with the specified translation
*
* @param dx The distance to translate in X
* @param dy The distance to translate in Y
*/
public void translate(float dx, float dy);可见canvas.translate()方法实现的操作是先乘(preconcat),等同于Matrix.preTranslate()。其实canvas中的矩阵变换方法rotate()、scale()、skew(),也是先乘操作。按照先乘的定义,先乘操作在初始矩阵的右边,那么多个先乘操作时,后面的先乘在前面的先乘右边。那么这时候你会发现,实际的运算式子刚刚好跟代码中的顺序一样,即M' = T(10,10) x R(θ) x T(-10,-10) x M,M表示初始矩阵。然后问题又来了,按照前面说的变换顺序,T(-10,-10)->R(θ)->T(10,10),又是跟代码相反的!难道我们要把代码反过来理解吗?
其实这里有两种方式,第一种,把运算式子写出来如M' = T(10,10) x R(θ) x T(-10,-10) x M,然后在按照从右边到左边的顺序(T(-10,-10)->R(θ)->T(10,10))去理解,改变的是坐标位置,坐标系不变。第二种,索性就从左边开始理解,这样既跟代码的顺序一致,也符合我们平时的阅读习惯,从左往右。
如果采用第二种方式去理解矩阵变换,就得改变变换的空间想象,这个时候改变得是坐标系,不变的是坐标位置,即坐标位置相对于它所在的坐标系里一直是不变的。如下是采用变换坐标系的空间想象去理解一开始的图形矩阵变换(灰色的是初始的坐标系)。
坐标系先平移了(10,10),然后把平移后的坐标系绕它的原点(0,0)旋转角度θ,再把变换后的坐标系沿着它自己的坐标轴方向平移(-10,10),最后在最终得到的坐标系里面绘出图形,这个过程中图形相对于它的坐标系的坐标位置一直保持不变。
可见最后实现的效果是一样的!对于一组矩阵变换操作,可以分别使用变换坐标位置和变换坐标系的空间想象去理解,没有哪个更优之说,无论采取哪种变换思想,首先第一步都是得明确实际的变换运算式子,然后再决定采取从左往右的变换坐标系的空间想象,还是采取从右往左的变换坐标位置的空间想象。
在这里,个人推荐使用变换坐标系的空间想象,因为这样可以做到通用,canvas和openGL里面的图形运算的矩阵操作都是先乘的,这样我们就可以按照代码的顺序去理解变换。像前面的Matrix的代码,我们可以让代码跟采用变换坐标系的空间想象的理解顺序一样。
matrix.preTranslate(10, 10);
matrix.preRotate(θ);
matrix.preTranslate(-10, -10);其实无论代码怎么写,只要运算式子是一样的即M' = T(10,10) x R(θ) x T(-10,-10) x M,实现的效果其实都是一样的!(上面的代码没有调用set方法,所以变换操作都是针对单位矩阵的,任何矩阵无论是左乘还是右乘以单位矩阵,都等于该矩阵,相当于数字乘法中的1的效果,所以这里表示运算顺序的式子中把单位矩阵忽略掉了。)
所以代码还可以这样写,刚好跟先乘的代码相反.
matrix.postTranslate(-10, -10);
matrix.postRotate(θ);
matrix.postTranslate(10, 10);所以重要的是知道运算式子,下面给出一个例子。
matrix.preScale(0.5f, 1);
matrix.preTranslate(10, 0);
matrix.postScale(0.8f, 1);
matrix.postTranslate(15, 0);
那么上面变换的实际运算式子是什么呢?先尝试自己写出来,再看下面的答案。(注意:后调用的pre操作更靠右,而后调用的post操作更靠左)
运算式子为:M = T(15,0) x S(0.8f,1) x S(0.5f,1) x T(10,0)
再写一段代码,在画布上画出一段文字,对其做一些旋转平移操作。
canvas.translate(100, 200);
canvas.rotate(90, 0, 0);
canvas.drawText("hello,world", 0, 0, mPaint);
试着画出最终的效果。
说了那么多矩阵变换的例子,似乎还没涉及到缩放变换,好,现在就给一个。
上面是原图,分别说出下面两段代码的变换效果。
matrix.preScale(2,2);
matrix.preTranslate(0,bitmapHeight); matrix.preTranslate(0, bitmapHeight * 2);
matrix.preScale(2, 2);其实上面的两个变换效果都是一样的!效果如下。
按照变换坐标系的空间想象,第一段代码,首先把坐标系放大两倍,然后把放大后的坐标系向下平移了一个图片高度(由于坐标系放大了,这个时候的高度实际是初始图片高度的两倍!)。第二段代码,首先将坐标系向下平移了两个图片高度,然后再把坐标系放大两倍。仔细想想,虽然它们的运算式子不一样,但它们的变换效果却是一样的!其实变换坐标系的空间想象可以结合现实中的世界地图,在地图上某个点到另一个点的距离是固定不变的,世界的范围也是不变的(也就是坐标位置固定不变),而之所以看到不同的大小的地图,是因为比例尺不一样,也就是绘制的坐标系的单位长度不一样。
最后,再说一个有趣的地方。其实View的onDraw(canvas)方法里的canvas(画布),在最初从根布局传下来时的原点就在屏幕的左上角,但传到当前view时,已经经过过裁剪(clip)和平移。裁剪的作用就是为了防止画出的内容超出的view的范围,而平移则是通过canvas.translate()实现,让画布的坐标系平移到当前view的原点,接下来在画布上的操作都是相对于这个原点的。所以就可以明白为什么当我们在view中绘图时,如果绘制的坐标是(0,0),图形出现在view的左上角,而不是屏幕的左上角。
Canvas还有两个常用的方法,save()和restore()。
/**
* Saves the current matrix and clip onto a private stack.
*
* Subsequent calls to translate,scale,rotate,skew,concat or clipRect,
* clipPath will all operate as usual, but when the balancing call to
* restore() is made, those calls will be forgotten, and the settings that
* existed before the save() will be reinstated.
*
* @return The value to pass to restoreToCount() to balance this save()
*/
public int save()
/**
* This call balances a previous call to save(), and is used to remove all
* modifications to the matrix/clip state since the last save call. It is
* an error to call restore() more times than save() was called.
*/
public void restore()save()方法就是保存当前的矩阵/裁剪状态。restore()就是把当前的矩阵/裁剪状态恢复到save()方法保存起来的那个状态下。也就是说 在save()和restore()方法之间做的矩阵变换或裁剪操作,在调用restore()方法后都不生效,画布恢复到save()方法之前的状态。
canvas.save(); // 保存状态(入栈)
canvas.translate(50, 0);
canvas.scale(2f, 2f);
mPaint.setColor(Color.BLUE); // 绘制蓝色方块
canvas.drawRect(0, 0, 50, 50, mPaint);
canvas.restore(); // 恢复状态(出栈)
mPaint.setColor(Color.GREEN); // 绘制绿色方块
canvas.drawRect(0, 0, 50, 50, mPaint);上面的代码效果如下。
可见在save()和restore()方法之间的变换操作并没有影响到绿色方块的绘制,它还是相对于save()之前的画布绘制自己。
好的,矩阵变换就这么多了!上面的所述并没有多少需要自己计算的地方,主要是靠理解矩阵在空间中如何变换的,空间形象力很重要。理解了之后,要实现一个图形的变换效果,那就容易多了!加油吧。