算法实验六:最大流应用,西瓜冰棍和最大流也有关系?图解三种最大流算法（Ford-Fulkerson方法，Edmons-Karp算法，Dinic算法）
文章目录
- 零、实验内容
- 一、初探最大流问题
- 二、解读论文评审问题(m=10,n=3)
- 三、Ford-Fulkerson方法
- 3.1 例子讲解（其中a>2,b>2）
- 反向边
- 得到论文分配方案
- 3.2 Ford-Fulkerson思维导图
- 3.3 伪代码
- 3.3.1 DFS寻找一条增广路径
- 3.3.2 Ford-Fulkerson全流程
- 四、EK (Edmons-Karp)算法
- 4.1 EK算法思维导图
- 4.2 伪代码
- 4.2.1 BFS算法
- 4.2.2 EK全过程
- 五、Dinic算法
- 5.1 整体思路
- 5.2 伪代码
- 5.2.1 Dinic_BFS
- 5.2.2 Dinic_DFS
- 5.2.3 Dinic整流程代码
- 六、性能分析（仅供参考）
- 6.1 分析评审个数n对于时间的影响
- 6.2 分析论文篇数m对于时间的影响
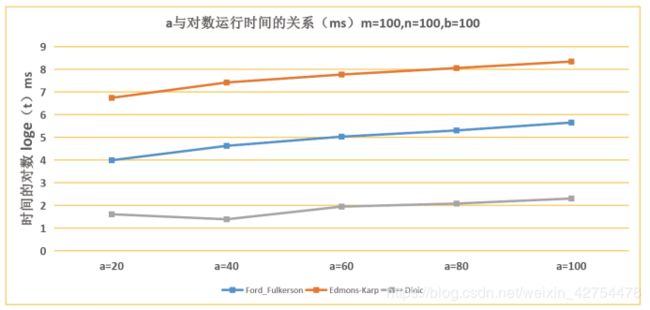
- 6.3 分析每篇论文需要的评审个数a对于时间的影响
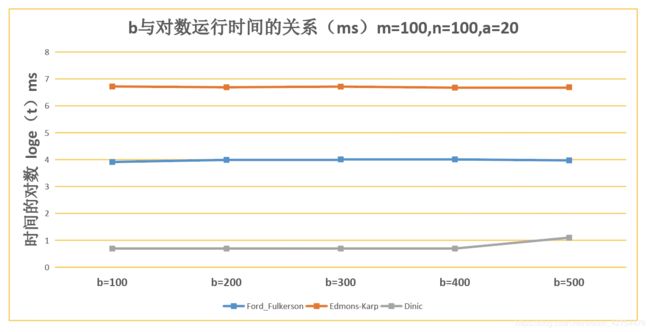
- 6.4 分析每个评审最多评的论文篇数b对于时间的影响
- 七、总结
本文主要介绍了三种计算最大流的算法，包括它们的整体思想，并且通过一个例子带你彻底弄懂残存网络的更新过程
零、实验内容
内容：论文评审问题
- 有m篇论文和n个评审，每篇论文需要安排a个评审，每个评审最多评b篇论文。请设计一个论文分配方案。
- 要求应用最大流解决上述问题，画出m=10，n=3的流网络图并解释说明流网络图与论文评审问题的关系。
- 编程实现所设计算法，计算a和b取不同值情况下的分配方案，如果没有可行方案则输出无解。
一、初探最大流问题
- 本题目属于最大流问题的一个应用问题，首先需要明确，在最大流问题中，我们谈论的是一个有向图，也就是说这道题目需要转换为图论问题来解决。
- 在最大流问题的有向图中，存在两个非常特殊的节点：源点(s),汇点(t).而本实验中涉及到的其他节点，都存在于从源点到汇点的某条路径上。
- 因此本实验一共包含四个变量，以及两个特殊节点，源点和汇点：
m：论文篇数
n：评审个数
a：每篇论文需要a个评审（不能够被同一个评委评多次）
b：每个评审最多评b篇论文
s：源点，其连接每一篇论文m，流量为a
t：汇点，其连接每一位评审，流量为b
二、解读论文评审问题(m=10,n=3)
在该论文评审问题上面，首先总共需要评审的论文数为a * m，评委能够评审的论文数为b * n，因此若能够分配所有论文，需要满足的第一个条件就是a * m≥b * n。
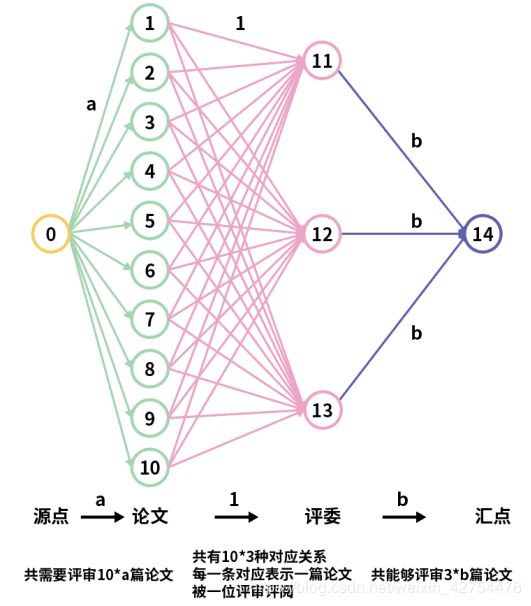
下面是对于10篇论文，3位评审的最大流图，下面进行详细解读：
- 按照最大流约定俗成的规则，该有向图的起点是源点，我们用0来表示
- 源点连接着10篇论文，我们用1-10来表示，由于每篇论文需要被评审a次，所以源点到论文的单向连接值为a，源点一共发出10*a的流量，表示所有论文需要被评审的总次数。
- 接着看论文->评委的连接，对于每一篇论文，它如果要被评审，无非就三种选择，被11号评委评审，或者被12号，13号评委评审。而每条论文->评委的连线表示某一篇论文被某一位评审评阅了一次，因此从论文->评委的单向连线值为1.因此总共有10*3=30条连线，表示总共有30种分配情况。
- 最后看评委->汇点的连接，因为一位评委能够评阅b篇论文，因此评委->汇点的单向连接值为b，而总共有3位评委，所以评委->汇点的总流量值为3*b。
OK，上面解读完了论文评审问题的最大流图中的节点关系，总结下来，该有向图一共有四层，源点->论文->评委->汇点。那么单单看这张图，该问题有解的条件是什么呢？
我们拿下面一张图来类比举例子。
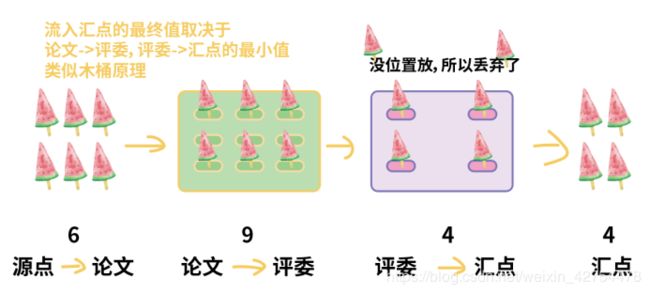
这是一个西瓜冰棍运送的过程，开始的时候一共有六根西瓜冰棍（类比上10*a的论文评审总数）。
接着首先用绿色容器从起点进行一次冷链运送，已知该容器能够装9根西瓜冰棍，因此开始的六根西瓜冰棍都能被装得下（类比上面论文到评委的3*10=30的流量）。
然后中途这些冰棍需要转到另一个容器进行第二次运送。已知第二个容器只能装4根冰棍（类比评委到汇点的3*b的流量），而绿色容器里面有6根冰棍，因此有两根冰棍将要被丢弃掉，最终只有4根西瓜冰棍运送到目的地（类比汇点）。
因此如果我们希望六根西瓜冰棍都能从起点运送到终点，那么中途的两个容器必须都能装得下这六根西瓜冰棍，否则只要其中一个装不下，就会有西瓜冰棍中途会被丢弃（类似木桶原理）。
回到最大流的问题中，如果所有论文都能够被评审，需要满足两个条件：
- 源点->论文的流量 ≤ 论文->评委的流量 （a * m ≤ m * n,即a≤n）
- 源点->论文的流量 ≤ 评委->汇点的流量 （a * m ≤ b * n）
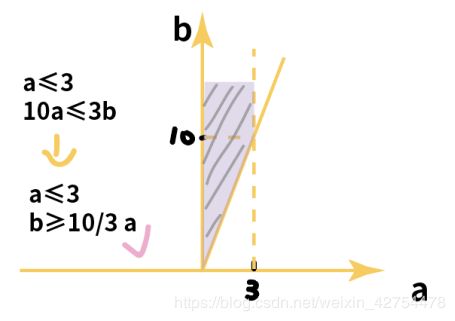
而上面的例子m=10，n=3，因此该问题有解的情况为a≤3且10a≤3b，根据下图解得紫色部分即为该问题的解。
三、Ford-Fulkerson方法
这是一个计算最大流的方法，之所以叫它方法而不是算法，是因为它提供了一种解决最大流问题的思想，基于这种思想，后续延伸出了很多其他最大流的解法，比如后面介绍的EK算法和Dinic算法，其实就是该方法的一个延伸。
该方法概况起来，就是在残存网络中不断寻找增广路径，每找到一条增广路径，就递增最大流f，并更新残存网络，直到残存网络中不存在增广路径，则此时f即为最终的最大流。
单看残存网络，增广路径的定义，也许很难看懂，所以下面我举了一个具体的例子带你一步步读懂它们的含义。看懂下面的过程，这个方法也就没什么难的了。
3.1 例子讲解（其中a>2,b>2）
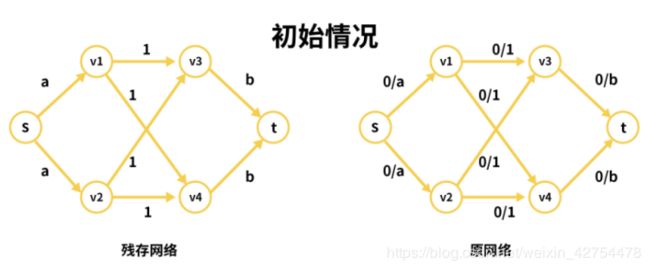
首先给出我们的初始残存网络和初始的原网络。与上面讲解的一样:
- 汇点s分别发出a流量给两篇论文v1和v2.
- 论文与评委之间存在2 X 2=4种情况，故有四条连线.
- 评委到汇点共有2 X b的流量。
先看残存网络，比如我们看s->v1这条路径，表示的含义为当前s到v1，剩余a流量可以通过。同理v1->v3，表示v1存在1的流量可通过v3.
再看原网络（只是为了方便理解起到一个参照作用，实际写代码我只用残存网络即可求出最大流，程序里面并没有原网络这个东西）。
‘/’左边的值表示已经通过的流量，’/’右边的值表示该路径的总流量。
比如s->v1这条路的值为0/a，表示当前通过的流量为0（因为还没开始为论文分配评委嘛），能通过的最大流量为a。
接下来就要开始找增广路径了。
首先需要明确，增广路径是在残存网络中从源点s到汇点t的一条路径。在该方法中，我们寻找路径是通过DFS进行寻找的，即对s进行DFS，若能到达t，则该路径为增广路径。
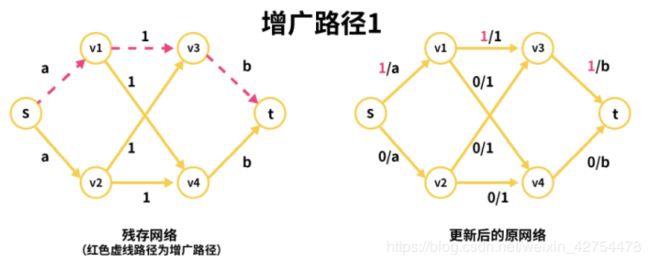
OK，我们看下面这张图（增广路径1），先从s出发，通过DFS找到s->v1->v3->t这条增广路径。这条增广路径涉及到三个值：a，1，b，根据上面冰棍的例子，即木桶原理,这三个值最小的是1，因此该增广路径的流量为1.我们看此时更新后的原网络，s->v1由原来的0/a变成1/a，表示这条路上已经经过了1的流量。同理v1->v3,v3->t的使用流量都变成了1.
找到了增广路径1之后，需要进行很关键的一步，更新残存网络。
在讲如何更新残存网络之前，先引入一个概念：反向边。
反向边
对于原残存网络中，我们的路径都是单向路径，表示当前能够通过的流量是多少。那么有没有可能存在这么一种情况，就是我分配论文给评委的过程中，发现有几篇论文分错了，导致最终的结果不好，然后我想撤回之前某一步的操作，换一种新的分配方法呢？这就是反向边的来源，它为我们计算最大流过程中提供了一个“撤回”的功能，其值表示的是已使用流量的值。
接着我们看下面这张图。更新一条边需要两步，拿s->v1这条边举例：
- 其原本剩余流量为a。因为在增广路径1中通过了1的流量，因此剩余流量需要减去1，变成a-1，表示此时s->v1剩余a-1的流量可以通过。
- 反向边的流量加上“减去的流量1”（默认一开始反向边的流量为0），因此v1->s表示我们有流量为1的撤回机会，我们用蓝色的边表示反向边。
同理
v1->v3（正向边）的值变为1-1=0
v3->v1(反向边)的值变为0+1=1
v3->t（正向边）的值变成b-1
t->v3 (反向边)的值也变成0+1=1
我们看下图中绿色文字的部分，表示的是增广路径1(s->v1->v3->t)更新残存网络之后的值。
上面讲完了增广路径1的寻找过程以及残存网络的更新。那接下来其实就是重复上面的过程了。
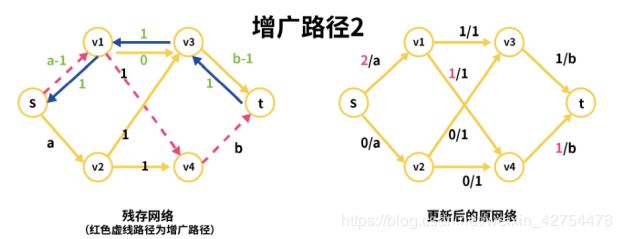
我们对下图的残存网络（经过上面增广路径1更新后的残存网络）寻找第二条增广路径s->v1->v4->t（粉红色虚线）。与第一条增广路径一样，该增广路径的流量为1（实际上该题目的所有增广路径流量均为1）
再看此时的原网络，s->v1的值由1/a变成了2/a，v1->v4由0/1变成1/1，v4->t由0/b变成1/b。
同理，我们看增广路径2(s->v1->v4->t)更新残存网络的过程（下图绿色文字部分）。
对于s->v1来说，由于此时通过了流量1，所以其剩余流量为(a-1)-1=a-2,反向边v1->s的为1+1=2,表示此时该边有两次撤回的机会(因为使用了两次).
同理
v1->v4（正向边）的剩余流量为1-1=0
v4->v1（反向边）的可撤回流量为0+1=1
v4->t（正向边）的剩余流量为b-1
t->v4（反向边）的可撤回流量为0+1=1
上面讲完了增广路径2的寻找过程以及残存网络的更新，接着就是寻找增广路径3。
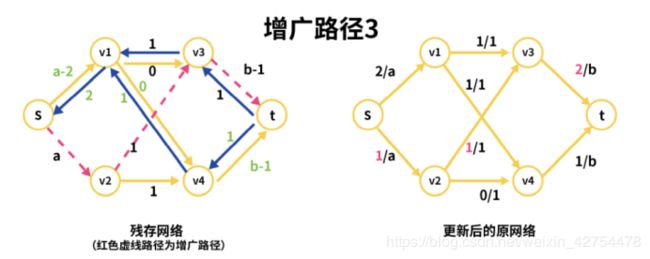
我们找到增广路径3为s->v2->v3->t (粉红色虚线）,同理上面两条路径，此时原网络进行了更新（粉红色文字），这里就不详细说了。
想提一点的是，为什么前两条路径都是s->v1,而这一条是s->v2？这是因为此时v1->v3=0,v1->v4=0,因此v1是没可能通向t的，所以我们才找v2（涉及到DFS的实现原理）。
下面来看增广路径3的残存网络更新（绿色文字部分），同前面一样，s->v2,v2->v3,v3->t这三条边的值减去1，其反向边的值加上1，不再细说。
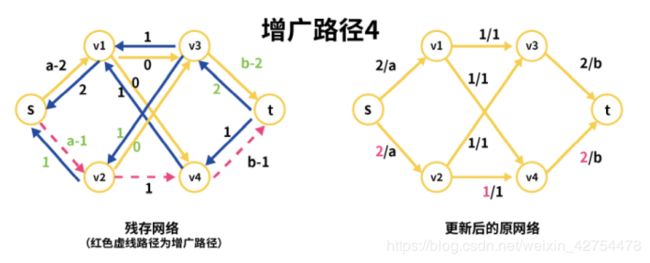
接着就是找到第四条增广路径s->v2->v4->t (粉红色虚线），同前面一样，不详细介绍每一步。
然后就是对增广路径4的残存网络更新（绿色文字部分）
可看到:
s->v2=a-1-1=a-2, v2->s=1+1=2.
v2->v4=1-1=0, v4->v2=0+1=1,
v4->t=b-1-1=b-1, t->v4=1+1=2
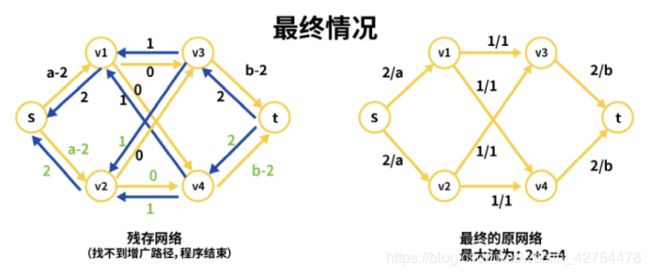
此时残存网络找不到任何一条增广路径，因此整个流程结束，得到最大流为4（四条增广路径，每条流量为1）.
得到论文分配方案
那么整个流程结束之后，论文的分配方案是什么呢？此时，对于每一位评委，我们看最终的残存网络中，该位评委到每一篇论文的连线（反向边）的有向值是否为1？若为1，则说明该论文被该评委评审过。
比如下图中的v3，我们看到v3->v1的值为1，说明v1这篇论文被v3评审过。
以此类推，v3这位评委负责的论文是：v1，v2；v4这位评委负责的论文是v1，v2.因此每篇论文都被评审两次。
在具体的代码实现中，只需要使用二重循环，对于每一位评委，都查看其与每一篇论文的有向值是否为零，进而得到整个论文分配方案。
3.2 Ford-Fulkerson思维导图
我是使用构建(m+n+2)*(m+n+2)的邻接矩阵的方式来做的，其中下标为0的节点表示源点，下标1->m的节点表示论文，下标m+1->m+n表示的是评委，下标m+n+1表示的是汇点t。
对于邻接矩阵的初始化，我们需要将源点到论文的有向边的值设置成a，将论文到评委的有向值设置成1，将评委到汇点的有向值设置成b。
整体的实现思路如下，其实就是不断从残存网络寻找增广路径的过程。
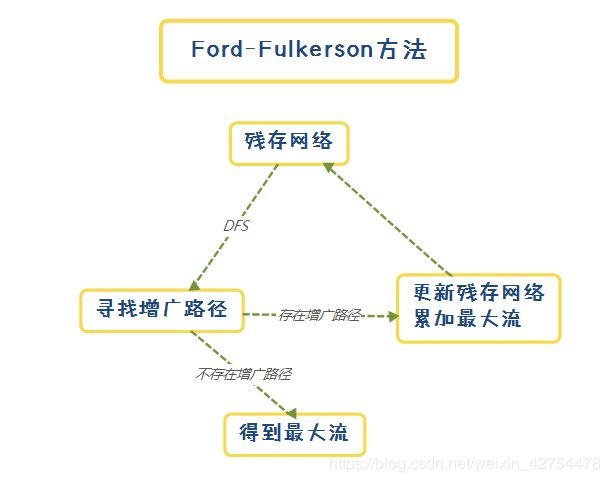
3.3 伪代码
3.3.1 DFS寻找一条增广路径
上面找到的是一条增广路径，而我们要不断寻找增广路径，下面是整个流程的伪代码：
3.3.2 Ford-Fulkerson全流程
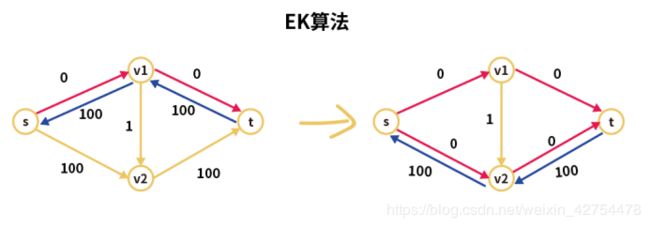
四、EK (Edmons-Karp)算法
EK算法的整体流程与Ford-Fulkerson方法一样，唯一的不同是EK算法使用BFS取代Ford-Fulkerson方法的DFS来寻找增广路径。
那么EK算法有什么优势呢？实际上它解决的是下面这个例子所面临的问题。在之前的方法中，如果使用DFS，可能会导致在某些特定情况下寻找增广路径的效率特别低，比如下面的这个例子，需要寻找200次才能完全找完所有增广路径。（可能你会问为什么第一次找的增广路径是s->v1,而第二次找的是s->v2而不是s->v1，这个是由DFS中节点访问顺序所决定的，这里只是说可能有这种情况会发生）
而使用EK算法的话，由于它是有层次的，所以就会避免上面的情况发生，只需要进行两次即可找到所有边这部分网上有非常多的的详细解释，这里我就抛砖引玉，具体的细节可以参考下别人的看法，或者参考《算法导论》的P426页，上面的解析非常清楚。
但实际上在论文——评委这道题目上我们不存在这样的竖边，所以也就不会有这种极端情况，因此在时间复杂度的测试时，会发现EK算法会比Ford-Fulkerson方法慢，因为在BFS实现中涉及到大量的节点压入队列，导致非常慢。
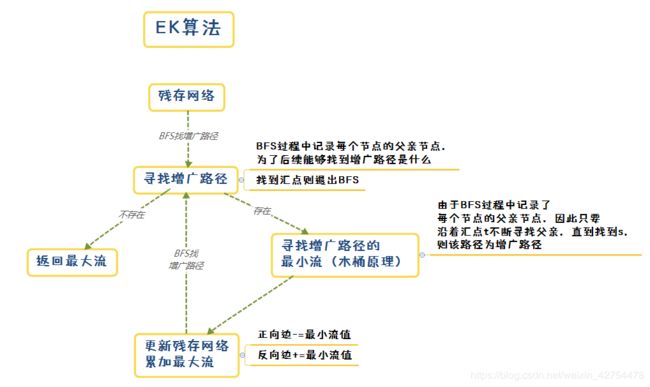
4.1 EK算法思维导图
整个流程就是不断寻找增广路径的过程，与DFS的过程不同，BFS需要先找到整条路径，再进行残存网络的更新，而DFS可以在递归的过程中把残存网络的更新完成。
因此为了能够在进行完BFS后能够找到我们的增广路径是什么，我们引入父亲节点数组，在BFS过程中，记录下每个节点的父亲节点。这样子当BFS结束后，若存在增广路径，则对汇点t进行反向寻父流程，直到找到源点s，则中途经过的节点都是增广路径上的节点。
同时在寻父亲过程中，记录该路径的最小流值（参照上面西瓜冰棍的例子）。
找到最小流之后，再次从汇点t反向寻父，这一次的目的是更新残存网络，即正向边减去最小流值，反向边加上最小流值。
至此，一条增广路径的寻找以及残存网络的更新结束。我们需要不断重复这个过程，直到找不到增广路径为止。
4.2 伪代码
4.2.1 BFS算法
4.2.2 EK全过程
五、Dinic算法
首先给出我对Dinic整个流程的思维导图理解：
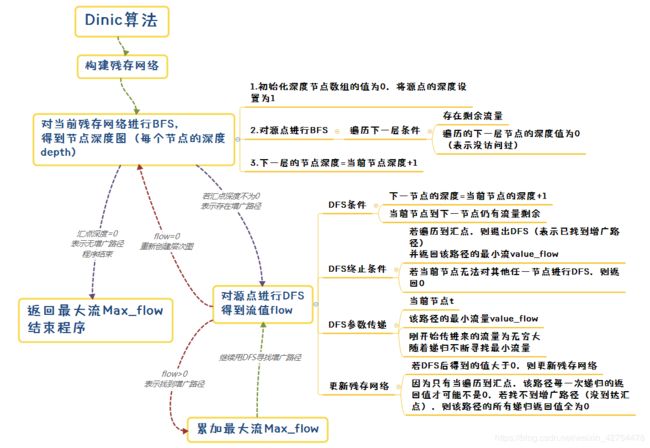
5.1 整体思路
- 首先构建初始的残存网络。
- 接着进行BFS构建深度图，用一个深度数组depth记录每个节点的遍历深度。
- 然后再对源点s不断进行DFS寻找增广路径。
（注意！该方法不需要常规DFS的访问数组visit，而是改用depth数组进行递归，递归条件为下一个节点的深度要等于当前节点的深度+1，才进行遍历，对于同深度或者低于当前节点的深度的节点，则不进行遍历。）
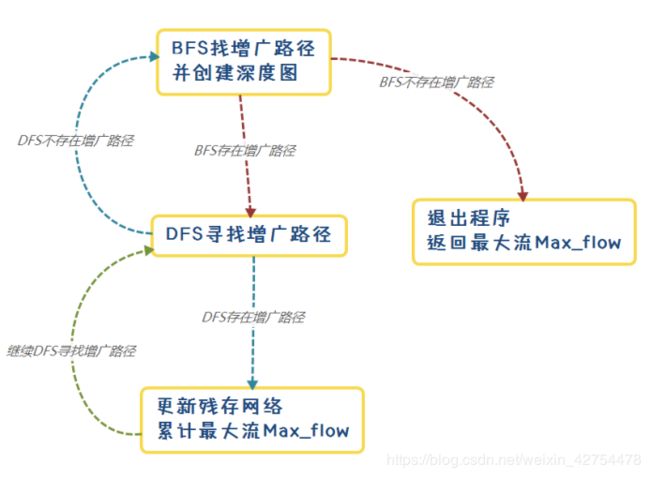
这么做的原因是，汇点t的深度一定是所有节点的深度中最大的，而增广路径的每个节点的深度是不断递增的，所以比起常规DFS的随意递归，该方法的递归更有针对性，即递归的每一步都是在靠着汇点t前进的。 - 如果对当前深度图进行DFS找不到增广路径，则重新进行一次BFS，创建新的深度图（由于DFS过程中会不断更新残存网络，因此这时BFS得到的深度图会发生变化），然后重复3的过程，继续寻找增广路径。如此往复。
- 如果进行BFS也找不到增广路径，说明此时整张图没有增广路径，则退出程序，返回最大流。
下面再用一张思维导图将BFS和DFS的关系弄清楚，其整体嵌套关系为BFS>DFS：
5.2 伪代码
5.2.1 Dinic_BFS
5.2.2 Dinic_DFS
5.2.3 Dinic整流程代码
六、性能分析（仅供参考）
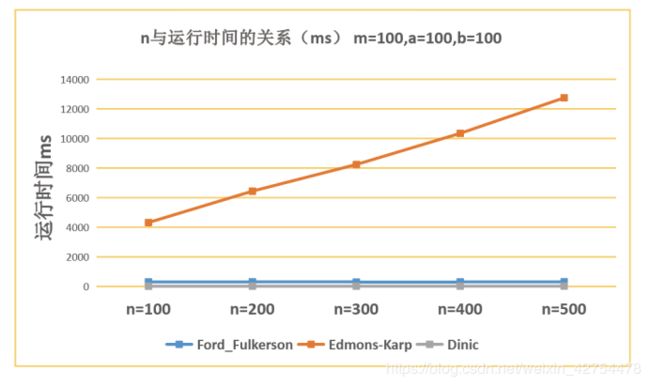
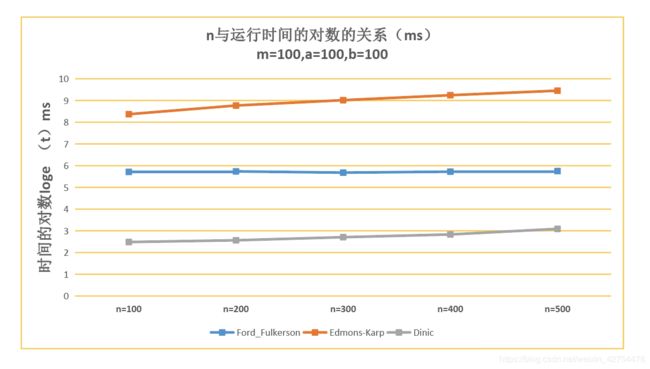
6.1 分析评审个数n对于时间的影响
- 随着n的增加，EK算法的时间成线性时间增加，而FF方法与Dinic算法的时间几乎不改变。
- 分析：由于EK算法使用的是BFS，而评委的个数的增多会导致BFS过程中对论文进行下一层遍历到评委的过程中压入队列的数量线性增长，因此运行时间自然增加。而DFS过程中不需要考虑节点的个数，因此时间不增加
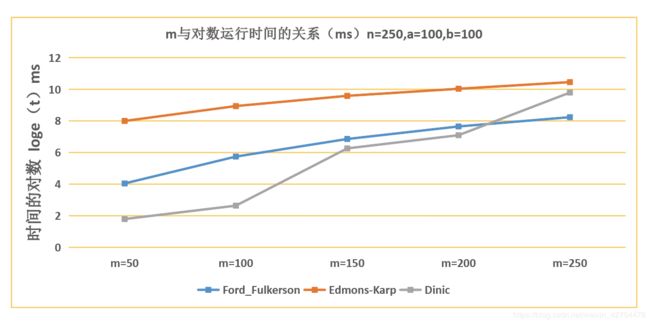
6.2 分析论文篇数m对于时间的影响
- 可见随着论文篇数的增加，三种方法的时间都是增加的。而在论文篇数较小的时候，Dinic算法与EK算法的效率差得不大，FF算法最慢。
- 当论文篇数较大的时候，Dinic的运行时间突然变得很大。
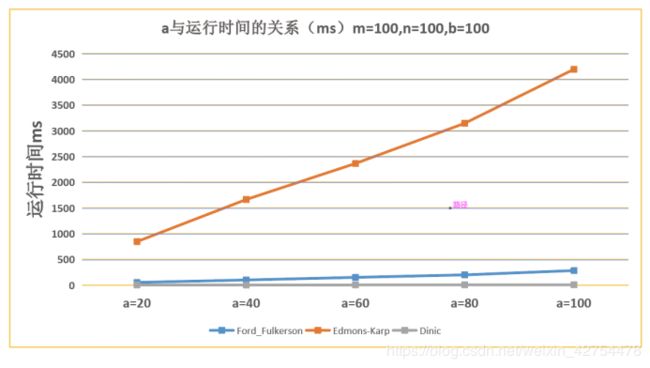
6.3 分析每篇论文需要的评审个数a对于时间的影响
- 可见随着a的增加，三种方法的时间都是会增加的，毕竟需要评审的论文篇数增加了。而EK算法与FF方法的时间增长是线性增长，Dinic的增长十分缓慢。
6.4 分析每个评审最多评的论文篇数b对于时间的影响
- 可见三种方法的运行时间均无变化
- 因为评审能够评阅的论文数跟时间没任何关系。
七、总结
总的来说，对于三种最大流算法，在该问题的情况下，Dinic的效率最快，Ford-Fulkerson方法第二快，Edmons-Karp算法最慢。
当然，还有非常多的最大流算法，比如最大二分匹配解决最大流问题（算法导论P428），sap算法等等，大家感兴趣可以自行了解。
如果觉得上面的过程解释得不清楚的话，大家可以在评论区留言，如果觉得本文还不错的话，也不妨点个赞支持一下噢！