【深度学习】为什么会存在激活函数？

来源：AINLPer微信公众号(点击了解一下吧)
编辑: ShuYini
校稿: ShuYini
时间: 2019-9-1

引言

    在深度学习网络中，我们经常可以看到对于某一个隐藏层节点的激活值计算一般分为两步，如下图：

    第一步，输入该节点的值为 $x_1$,$x_2$时，在进入这个隐藏节点后，会先进行一个线性变换，计算出值 $z^{[1]}=w_1{x}_1+w_2{x}_2+b^{[1]}=W^{[1]}x+b^{[1]}$，上标 1 表示第 1 层隐藏层。
    第二步，再进行一个非线性变换，也就是经过非线性激活函数，计算出该节点的输出值(激活值) $a^{(1)}=g(z^{(1)})$，其中 g(z)为非线性函数。
    那么问题来了，这个激活函数到底有什么用呢，可不可以不加激活函数呢？

什么是激活函数？

    激活函数是神经网络中极其重要的概念。它们决定了某个神经元是否被激活，这个神经元接受到的信息是否是有用的，是否该留下或者是该抛弃。激活函数的形式如下：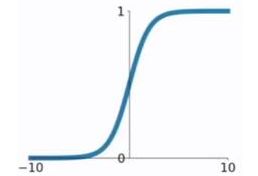
    激活函数是我们对输入做的一种非线性的转换。转换的结果输出，并当作下一个隐藏层的输入。

如果没有激活函数会怎样？

    1、首先对于y=ax+b 这样的函数，当x的输入很大时，y的输出也是无限大/小的，经过多层网络叠加后，值更加膨胀的没边了，这显然不符合我们的预期，很多情况下我们希望的输出是一个概率。
    2、线性变换太简单（只是加权偏移），限制了对复杂任务的处理能力。没有激活函数的神经网络就是一个线性回归模型。激活函数做的非线性变换可以使得神经网络处理非常复杂的任务。例如，我们希望我们的神经网络可以对语言翻译和图像分类做操作，这就需要非线性转换。同时，激活函数也使得反向传播算法变的可能。因为，这时候梯度和误差会被同时用来更新权重和偏移。没有可微分的线性函数，这就不可能了。
    3、结论：可以用线性激活函数的地方一般会是输出层。

常用的激活函数有哪些？

    在深度学习中，常用的激活函数主要有：sigmoid函数，tanh函数，ReLU函数、Leaky ReLU函数。

sigmoid函数

    该函数是将取值为 (−∞,+∞)(的数映射到 (0,1) 之间。sigmoid函数的公式以及图形如下：
$$g(z)=\frac{1}{1+e^{-z}}$$    对于sigmoid函数的求导推导为：    sigmoid函数作为非线性激活函数，但是其并不被经常使用，它具有以下几个缺点：
    （1）当 zz 值非常大或者非常小时，通过上图我们可以看到，sigmoid函数的导数 g′(z) 将接近0 。这会导致权重W的梯度将接近0，使得梯度更新十分缓慢，即梯度消失。
    （2）函数的输出不是以0为均值，将不便于下层的计算，具体可参考[3]。sigmoid函数可用在网络最后一层，作为输出层进行二分类，尽量不要使用在隐藏层。

tanh函数

    tanh函数相较于sigmoid函数要常见一些，该函数是将取值为 (−∞,+∞)的数映射到 (−1,1) 之间，其公式与图形为
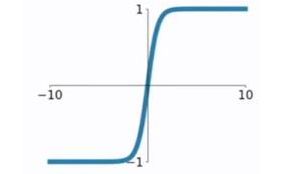$$g(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$    tanh函数在0附近很短一段区域内可看做线性的。由于tanh函数均值为0，因此弥补了sigmoid函数均值为0.5的缺点。对于tanh函数的求导推导为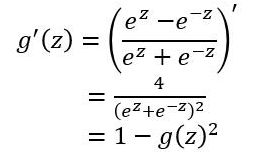：    tanh函数的缺点同sigmoid函数的第一个缺点一样，当 zz 很大或很小时，g′(z)接近于0，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

ReLU函数

    ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。ReLU函数的公式以及图形如下：
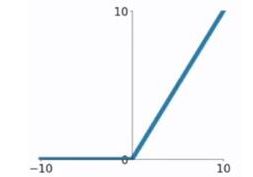$$g(z)=\{\begin{array}{ll}z,& \text{if z>0 }\\ 0,& \text{if z<0}\end{array}$$对于ReLU函数的求导为：
$$g^{\prime }(z)=\{\begin{array}{ll}1,& \text{if z>0 }\\ 0,& \text{if z<0}\end{array}$$
    ReLU函数的优点：
    （1）在输入为正数的时候（对于大多数输入 zz 空间来说），不存在梯度消失问题。
    （2） 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）
    ReLU函数的缺点：
    （1）当输入为负时，梯度为0，会产生梯度消失问题。

Leaky ReLU函数

    这是一种对ReLU函数改进的函数，又称为PReLU函数，但其并不常用。其公式与图形如下：
$$g(z)=\{\begin{array}{ll}z,& \text{if z>0 }\\ az,& \text{if z<0}\end{array}$$    其中 a 取值在 (0,1)之间。Leaky ReLU函数的导数为：
$$g(z)=\{\begin{array}{ll}1,& \text{if z>0 }\\ a,& \text{if z<0}\end{array}$$     Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。

参考文献

[1] https://blog.csdn.net/qq_35290785/article/details/89349635
[2] https://www.datalearner.com/blog/1051508750742453
[3] https://www.cnblogs.com/lliuye/p/9486500.html

更多自然语言处理、pytorch相关知识，还请关注 AINLPer 公众号，极品干货即刻送达。