PCA与KPCA

PCA是利用特征的协方差矩阵判断变量间的方差一致性，寻找出变量之间的最佳的线性组合，来代替特征，从而达到降维的目的，但从其定义和计算方式中就可以看出，这是一种线性降维的方法，如果特征之间的关系是非线性的，用线性关系去刻画他们就会显得低效，KPCA正是应此而生，KPCA利用核化的思想，将样本的空间映射到更高维度的空间，再利用这个更高的维度空间进行线性降维。

如果样本的维度是k，样本个数是n（n>k），那么首先需要将样本投射到n维空间，这个n维空间是这样计算的：首先计算n个样本间的距离矩阵D（n*n），核函数F，则F(D)就是他的高维空间投射。

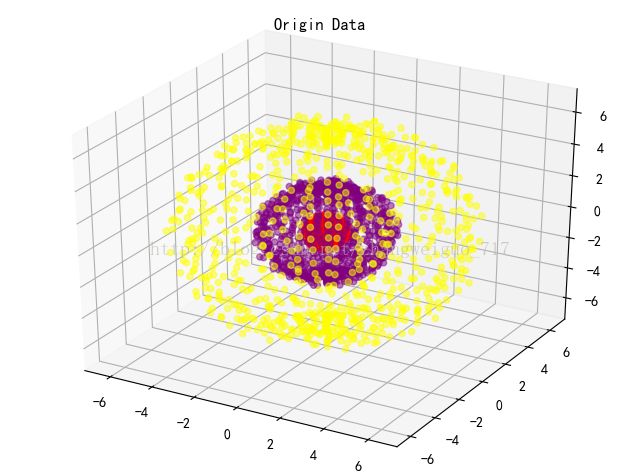
我们用几个例子来看KPCA与PCA的不同：我们用三维空间中三个同心球面来作为三类原始数据，用不同的核函数来将其降维到二维平面，当核函数是linear（线性）时，就是PCA，其他的核函数，如RBF，SIGMOID，多项式等，都是非常常用的核化函数。

原始数据分布点如下，共2700个样本，每一类样本900个：

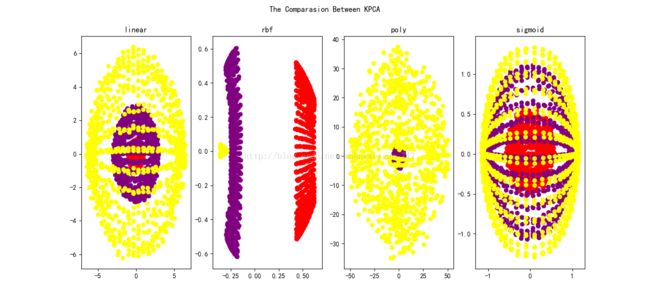
用KPCA各类核函数将其降维后，达到效果如下：

很明显，RBF核能将不同类别的数据分开，而PCA只是将其做了一个投影，在这里，由于三个球是相互嵌套的，很难找到合适的投影方向，将三类数据很好的分开，由此造成了非常差的表现，KPCA的优点由此可见。

# -*-encoding:utf-8 -*-
from time import time
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import colors
from mpl_toolkits.mplot3d import Axes3D as ax3
from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits,fetch_olivetti_faces,load_digits

from sklearn.decomposition import PCA
from sklearn.preprocessing import scale,StandardScaler
from sklearn import decomposition
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False



color=['red','purple','yellow']
for i in colors.cnames:
    if i in color:
        pass
    else:
        color.append(i)


def generate_circle_data3():
    xx=np.zeros((2700,3))
    x1=np.ones((900,))+0.5*np.random.rand(900)-0.5
    r1=np.linspace(0,2*np.pi,30)
    r2=np.linspace(0,np.pi,30)
    r1,r2=np.meshgrid(r1,r2)
    r1=r1.ravel()
    r2=r2.ravel()
    xx[0:900,0]=x1*np.sin(r1)*np.sin(r2)
    xx[0:900,1]=x1*np.cos(r1)*np.sin(r2)
    xx[0:900,2]=x1*np.cos(r2)
    x1=3*np.ones((900,))+0.6*np.random.rand(900)-0.6
    xx[900:1800,0]=x1*np.sin(r1)*np.sin(r2)
    xx[900:1800,1]=x1*np.cos(r1)*np.sin(r2)
    xx[900:1800,2]=x1*np.cos(r2)
    x1=6*np.ones((900,))+1.1*np.random.rand(900)-0.6
    xx[1800:2700,0]=x1*np.sin(r1)*np.sin(r2)
    xx[1800:2700,1]=x1*np.cos(r1)*np.sin(r2)
    xx[1800:2700,2]=x1*np.cos(r2)
    target=np.zeros((2700,))
    target[0:900]=0
    target[900:1800]=1
    target[1800:2700]=2
    target=target.astype('int')
    return xx,target  

def compare_KPCA():
    data,target=generate_circle_data3()
    pca=decomposition.PCA(n_components=2)
    data1=pca.fit_transform(data)
    try:
        figure1=plt.figure(1)
        ax=ax3(figure1)
        ax.scatter3D(data[:,0],data[:,1],data[:,2],c=[color[i] for i in target],alpha=0.5)
        plt.title('Origin Data')
    except:
        pass
    
    figure2=plt.figure(2)
    k=1
    for kernel in ['linear','rbf','poly','sigmoid']:
        plt.subplot(1,4,k)
        k+=1
        kpca=decomposition.KernelPCA(n_components=2,kernel=kernel)
        data2=kpca.fit_transform(data)
        plt.scatter(data2[:,0],data2[:,1],c=[color[i] for i in target])
        plt.title(kernel)
    plt.suptitle('The Comparasion Between KPCA')
    plt.show()





def bench_k_means(estimator, name, data,labels):
    t0 = time()
    estimator.fit(data)
    print('%-9s\t%.2fs\t%i\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f'
          % (name, (time() - t0), estimator.inertia_,
             metrics.homogeneity_score(labels, estimator.labels_),
             metrics.completeness_score(labels, estimator.labels_),
             metrics.v_measure_score(labels, estimator.labels_),
             metrics.adjusted_rand_score(labels, estimator.labels_),
             metrics.adjusted_mutual_info_score(labels,  estimator.labels_),
             metrics.silhouette_score(data, estimator.labels_,
                                      metric='euclidean')))

compare_KPCA()