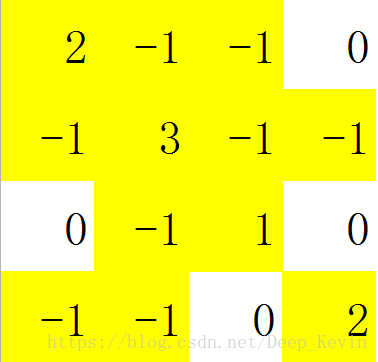Matrix-Tree定理及其拓展
正题
不能再半途而废了。
让我们现在开始讲一下Matirx-Tree定理。
其实这个定理是用来解决关于“用图建树的方案树”之类的问题的。
首先我们要了解几个定理及其证明。
1.我们定义一个n*n的矩阵A,它的行列式为
p是1到n的一个排列,laowang(p)指的是其中的逆序对个数。其实就是排列一个p使得后面行列不相交
2.那我们根据定义式,就可以知道,任意交换两行i,j,行列式就会乘上-1.
因为交换i,j两行的时候,其他的行都是不变的,我们把这单独两行提出来,就会发现逆序对的改变都会恰好![]() 。所以我们就知道,行列式会变为原来的相反数。
。所以我们就知道,行列式会变为原来的相反数。
3.接着,我们还要推导一个东西,当有两行一样时,行列式为0.
比如说这两行是i,j,首先不讨论这两行,也就是说把这两行先提出来,我们就会发现,当![]() 时,我们可以知道,行列式的符号是不用改变的,因为不存在逆序对,也就是说行列式是
时,我们可以知道,行列式的符号是不用改变的,因为不存在逆序对,也就是说行列式是![]() ,而当
,而当![]() 的时候,行列式的符号改变了,所以行列式是
的时候,行列式的符号改变了,所以行列式是![]() ,又因为i,j两行完全相同,所以说,加/减的东西也相同。
,又因为i,j两行完全相同,所以说,加/减的东西也相同。
4.下一个,当一行的数全部乘上了一个k,行列式也乘上k。
显然的,你直接把中间某一项乘k,再把k提出来即可。
5.当某一行是另一行的k倍,行列式为0.(k!=0)
比如说我们当前的行列式是det,把一行乘k,行列式为k*det,又因为现在两行都相同,所以k*det=0,又因为k!=0 ,所以det必为0.
6.当某一行加上另一行的k倍时,行列式不变。
因为行列式具有简单的"分配律",你给第i行都加上第j行的k倍(逐位加),就相当于,把整个矩阵的复制一遍,把其中第i行挖空,再填入第j行的k,然后把两个矩阵的行列式相加,这样很明显是可以成立的,因为相当于你把第i行拆开来罢了。
我们就可以用第6条定理完成![]() 求解行列式。
求解行列式。
怎么求呢。。。
首先我们要有一个构造的n*n的矩阵。
像上面这个图,空出的位置都是0,现在我们如何利用第6条定理,把他转化为下图呢?
黄色表示有数,0表示这个数字为0,很多人想问为什么要化成这个样子,因为这时,行列式就是对角线的乘积,即为![]() 。因为除了这个取法,一定会包括一个因子0。
。因为除了这个取法,一定会包括一个因子0。
所以我们试着去构造这样一个矩阵
for(int j=1;j<=n;j++){
for(int i=j+1;i<=n;i++)
while(d[i][j]){
long long temp=d[j][j]/d[i][j];
for(int k=j;k<=n;k++)
d[j][k]=(d[j][k]-d[i][k]*temp%Mod+Mod)%Mod,swap(d[j][k],d[i][k]);
ans*=-1;
}
ans*=d[j][j];
ans%=Mod;
}我们试着辗转相除来解决这个问题,因为一行可以加上或减去另一行的k倍,所以我们联想到了辗转相除。我们不断地拿第j行第j列中的元素出来,让它与下面的元素比较,直到把他下面的全部变为0。那我们一个一个操作,对于d[j][j]和d[i][j](i>=j+1)
我们不断将两行辗转相除,并且交换,交换的代价就是-1;
最后我们把对角线乘起来就是答案。
拓展
我们光知道这个还不行,我们还需要知道这个东西可以解决什么问题。
无向图
1.n个点m条边的一张没有重边,没有子环的图,保证联通,求生成树个数。
我们构造一个n*n的矩阵A,对于A[i][j]来说,当 i==j 时,A[i][j]存的是i点的度数(无向图)。当i != j 时,存的是i,j之间是否有边,有边为-1,没边就是0.
然后我们把任意的第i行和第i列挖掉,把剩下的向左上对齐,求剩下矩阵的行列式即可。(我太菜了,不知道证明)。
有向图
2.求外向树,把d[i][i]改成一个点的入度即可。
3.求内向树,把d[i][i]改成一个点的出度即可。
当然要像无向图那样存边和求行列式。
呼啊,说完了