SQL数据库——关系代数(一)及解题套路

数据库的类型

我们一般会把数据库简单区分成关系型数据库(SQL)和非关系型数据库(NoSQL)。

关系型数据库：MySQL、MariaDB、PostgreSQL、Oracle、SQL Server。比较有意思的是关系型数据库的logo很多都是动物。

非关系型数据库：一般只需要知道两个——Redis和MongoDB。Redis是键值类型(Key-Value)的数据库，类似JAVA里的Collection类的Map，默认情况下Redis很难进行类似SQL里的where和级联select操作；MongoDB被称作文档型数据库，介于SQL和Redis之间，它没有表(Table)的结构，你想怎么插入就怎么插入，但是可以进行级联条件查询等操作。

关系型数据库的关系

记$R(A_1,A_2,...)$为关系模式，其中$R$为关系名，$A_1$等为组成该关系的属性名集合。

关系模式的详细表示为$R(U,D,DOM,F)$——$U$即为$A_1,A_2$；$D$为$U$中属性来自的域；$DOM$为属性$U$向域$D$的映射集合；$F$为依赖关系，如主键、外键等。但根据考试经验，这玩意一般用不到。

可以简单把$R$理解成一个表，$A_1$等为属性列的名字。如一个学生信息表：学生信息表(学号，性别，生日，专业，姓名...)。这样的理解方式有助于后面对连接操作的理解。

表里的每个值被称为元组，即所谓的“行”。

关系代数

关系代数是关系型数据库所完备的一类数学逻辑。其基本运算符有：

集合/逻辑运算符	含义	比较运算符	含义
$\cup$ / $\vee$	并/或	$>$	大于
$\cap$ / $\wedge$	交/与	<	小于
$\times$	笛卡尔积	$\le$	小等于
-	差	$\ge$	大等于
$\neg$	非	=	等于

特殊操作还有四个：

运算符	含义	运算符	含义
$\sigma$ (读作"“希格玛”")	选择	$\pi$ 或 $\prod$	投影
$\bowtie$ (读作"join")	(自然)连接	$÷$	除

涉及到连接，除了自然连接$\bowtie$，就必须提到几种扩展连接方式：

运算符	含义	运算符	含义
${\bowtie }_C$	$\theta$连接(条件连接)	$\stackrel{o}{\bowtie }$	自然连接
${\stackrel{o}{\bowtie }}_L$	左外连接	${\stackrel{o}{\bowtie }}_R$	右外连接

这几种连接方式将在后面和笛卡尔积做集中区分。

理解关系代数符号

从一道例题出发：

① 投影

要理解 ${\pi }_{A_1,A_4}({\sigma }_{A_2{<}^{\prime }2017^{\prime }\wedge A_4{=}^{\prime }95^{\prime }}(R\bowtie S))$ 就要先从投影说起。

$\pi$ 或 $\prod$ 被称为投影操作，但我更偏向于把它称为去冗。

什么是投影？假设我现在有两个表：学生信息(学号，姓名，班级)和学生成绩(学号，成绩，班级)，如果以学号、姓名、班级、成绩为四个轴建立坐标系，两个表中同一个学生的信息会被映射到两个点。举一个例值：

(左)学号	(左)姓名	(左)班级	(右)学号	(右)成绩	(右)班级
32	张三	1401032	32	90	1401032

你会发现学号和班级在左右两个表中都重合了，如果我们只看两个表中的学号和班级，那么左右两个表中的这个值都会是一样的，也就是被投影到了同一个点——

(左)学号	(左)姓名	(左)班级	(右)学号	(右)成绩	(右)班级
32	张三	1401032	32	90	1401032

如果每一个学生都有成绩或每一个有成绩的学生都登记到学生信息表中，那么：

$${\pi }_{学号，班级}学生信息(学号，姓名，班级)={\pi }_{学号，班级}学生成绩(学号，成绩，班级)$$

---

之所以说投影就是去冗，我们画个图会更直观点，给出两个关系R(X,Y)——

X的值	Y的值
1	2
1	3
2	2

制图如下:

如果做${\sigma }_X(R)$操作，则前两个点(绿线)则会投影到同一个地方，也就完成了一次“去冗”，丢掉了我们所不关心的Y轴信息；如果做${\sigma }_Y(R)$操作，则第一和第三个点(黄线)也被投影到同一个点。用SQL语句就是：select distinct X from R。

当我们通过select操作选择出一堆数据时，难免会有不少如点(1,3,...)和点(1,2,...)这样的结果值，我们现在只想知道它们在X轴上等于几，则直接对X轴投影，即可只得到一个(1)...。

注意，投影会改变数据的维度，比如上面例子中两列的表经过投影只留下了一个属性列。

---

特殊的，有若干个表经过复杂的操作(连接、选择等等)，可能会产生两条一摸一样的数据，这时候使用符号$\delta (R)$(读作“德尔塔”)表示去除R中相同的元组(值、行、数据)。

② 选择

$\sigma$和$\pi$都有特殊记法，如题目中的 ${\sigma }_{A_1}(R)$ 指的是选择R关系中的$A_1$属性列，略去属性列名而采用列序号表示，等价于${\sigma }_1(R)$。配合比较、集合/逻辑运算符等，则可以进一步附加选择时的条件，如：${\sigma }_{A_1{>}^{\prime }2017^{\prime }}(R)$。

选择的SQL语句为：select A1 from R [where ....]。这部分内容比较简单，主要需要了解的就是刚刚提到的特殊记法，会在很多题目中出现。

③ 连接

连接是一个非常复杂的问题，主要有四种：自然连接、条件连接、左外连接和右外连接。同时还会有一个笛卡尔积在其中混淆视听。

1.笛卡尔积

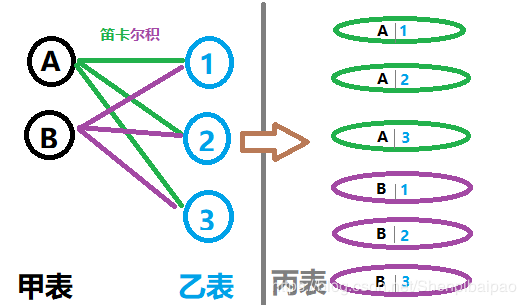
笛卡尔积和连接最大的区别在于：不会合并任何一个列(属性)，而是完整地做了一次排列组合操作。用图来表示：(图中A、B、1、2、3均为表的某个值，甲表和乙表做笛卡尔乘积( $\times$ )得到丙表，甲表和乙表有且只有一列属性列，以黑/蓝圆圈表示)

假如有$R(A_1,A_2,A_3)$和$S(A_2,A_3,A_4)$，则$R\times S$ 等于$R_S(A_1,A_2^R,A_3^R,A_2^S,A_3^S,A_4)$共$3+3=6$列，如果R中有7条数据，S中有8条数据，$R_S$中会有$7\times 8=56$条数据。

这时候我们反过来想一下，如果做${\pi }_{黑圆圈}(R\times S)$，就又经过投影得到了甲表。

2.自然连接

自然连接和笛卡尔积的区别在于，会合并相同的列，并以相同的列的值作为两个表的合并依据。

上图中甲表和乙表由于不存在相同的值和列，因此做自然连接会得到一个空表。

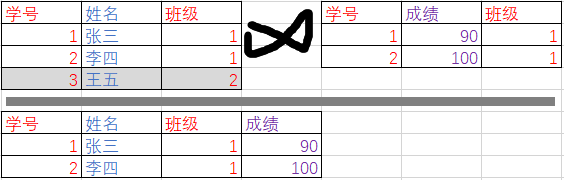
以学生信息(学号，姓名，班级)和学生成绩(学号，成绩，班级)这两个表为例，做它们的自然连接$\bowtie$：

注意到学生信息表中的王五的信息由于没法跟学生成绩表中找到(学号，班级)的匹配，因此在合成表中直接被删除了（理解成王五缺考了）。我们把这种找不到匹配的值叫做悬浮元组，悬浮元组会在左右外连接中用到。

同样，对这个合成后的表做${\pi }_{班级}$去冗操作，就会得知没有缺考的人都是1班的(简化一下问题，我们假设已知只有两个班级且有一个班级的人全部缺考了)。

3.条件连接($\theta$ 连接)

条件连接是一种先经过笛卡尔乘积再进行选择的操作，例如上文中学生信息和学生成绩的例子(分别记为R和S)：(别忘了上文中提到的——$\sigma$和$\pi$都有特殊记法)

$$R\bowtie S\approx {\sigma }_{1=4\wedge 3=6}(R\times S)=R{\bowtie }_{\underset{学号与班级相同}{C}}S$$

显然 ，等值条件连接可以产生与自然连接相近的结果，但依旧会保留一些冗余的列(这也是笛卡尔乘积与自然连接最大的差距之处)；大部分情况下，这种冗余无法通过$\pi$消除，详见下图。

我们画个图：

同样，条件可以有很多种，上面的例子是左右表学号和班级相同，你也可以只单单把条件设为成绩大于95，即$R{\bowtie }_{\underset{成绩{>}^{\prime }95^{\prime }}{C}}S$ ，那么最终结果就是：(显然这种$\theta$连接出来的结果并不能反映学生成绩的真实意义，除非再做一次比对班级学号的选择)

学号	姓名	班级	学号	成绩	班级
1	张三	1	2	100	1
2	李四	1	2	100	1
3	王五	2	2	100	1

等值连接：$R{\bowtie }_{\underset{学号与班级相同}{C}}S$就是等值连接，是条件连接的一个特例。与自然连接不同，虽然都需要寻找等值的属性，但不像自然连接一样只保留一个同名属性列。

4.外连接

外连接分为左/右外连接。某种意义上，可以把外连接看成是自然连接的一种扩充。

上文中提到了悬浮元组，还是以学生信息和学生成绩为例子，在自然连接中，悬浮元组会被直接丢弃，而外连接则会根据左右情况予以保留。

例如:

会发现左表的悬浮元组在左外连接中得以保留，右表由于没有悬浮元组，因此右外连接时和自然连接结果相同。其SQL语句一般为：select A1 from R left join S on R.学号=S.学号 and R.班级=S.班级。

---

除此之外还有全外连接(full join)，即同时保留两边的悬浮元素，在以上例子中，全外连接的结果和左外连接相同，符号一般为：$\stackrel{o}{\bowtie }$，不是很重要。

5.自连接

除此之外还有一种叫自连接的操作，刚刚在选择连接中提到：

$$R\bowtie S\approx {\sigma }_{1=4\wedge 3=6}(R\times S)=R{\bowtie }_{\underset{学号与班级相同}{C}}S$$

之所以是近似相等就是因为保留了R的学号、班级和S的学号、班级这些冗余信息，且无法使用$\pi$消除，那么使用自连接就可以把它变成完全相等。

自连接不引入任何新符号，相应的SQL语句如：select * from R as a, R as b where a.A1=b.A1。仅作了解即可。

例题求解

回到刚刚所说的例题：

求${\pi }_{A_1,A_4}({\sigma }_{A_2{<}^{\prime }2017^{\prime }\wedge A_4{=}^{\prime }95^{\prime }}(R\bowtie S))$等价为…?

• 用人话来解释这个式子，就是R和S自然连接后，选择满足$A_2$小于2017和$A_4$=95的数据，然后只保留$A_1$和$A_4$中不重复的值，最终关系的结构为$R_f(A_1,A_4)$。

先看第一个选项，我们应当知道$R\bowtie S$形成的新关系为$R_S(A_1,A_2,A_3,A_4)$，其中自然连接消去(合并)了二者中相同的$A_2,A_3$属性列，那么根据$\sigma$的特殊记法，此处的${\sigma }_{2{<}^{\prime }2017^{\prime }\vee 4{=}^{\prime }95^{\prime }}$等价于${\sigma }_{A_2{<}^{\prime }2017^{\prime }\vee A_4{=}^{\prime }95^{\prime }}$，对比原式显然错误(逻辑错误)。

再看第二、三个选项。根据$\sigma$的特殊记法，首先排除C答案。因为S关系只有三个属性列，而${\sigma }_{6{=}^{\prime }95^{\prime }}(S)$显然不能成立。

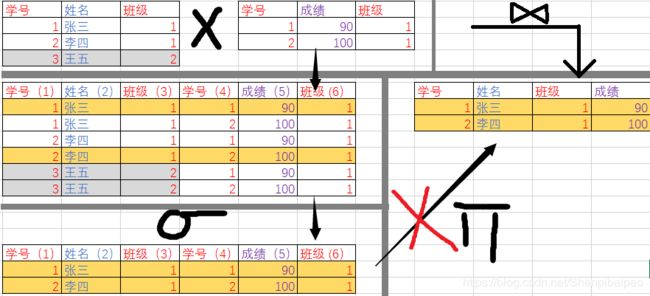
接着，先来想想笛卡尔乘积后$R\times S$会变成什么样的结构。
显然其结构为$R_S(A_1,A_2^R,A_3^R,A_2^S,A_3^S,A_4)$，共六个属性列。
第二个选项中${\sigma }_{2{<}^{\prime }2017^{\prime }}(R)\times {\sigma }_{3{=}^{\prime }95^{\prime }}(S)$ 其实是${\sigma }_{A_2{<}^{\prime }2017^{\prime }}(R)\times {\sigma }_{A_4{=}^{\prime }95^{\prime }}(S)$，从语义上来说也是选择满足$A_2$小于2017和$A_4$=95的数据，并通过最外层的投影${\pi }_{1,6}$完成了$R_f(A_1,A_4)$的映射。

• 另外，一个比较常见的化简是：${\sigma }_{A_2{<}^{\prime }2017^{\prime }}(R)\times {\sigma }_{A_4{=}^{\prime }95^{\prime }}(S)$等价于${\sigma }_{A_2{<}^{\prime }2017^{\prime }\wedge A_4{=}^{\prime }95^{\prime }}(R\times S)$。

但别忘了笛卡尔乘积不会根据相同值进行匹配消去相同属性列。所以，第四个选项和第二个选项相比较，多了${\sigma }_{2=4\wedge 3=5}$的操作，在笛卡尔乘积之后手动进行了选择，即一次等值$\theta$连接，让其近似相等于自然连接。

综合以上，做这种题的思路大概就是：

1. 把原式最终得到的关系$R_f(U)$写出来
2. 把跟原式与或非逻辑不相符合的逻辑错误选项淘汰
3. 根据最终关系$R_f$淘汰不合理的选项
4. 处理映射、选择中的逻辑陷阱。常见的陷进如上文中的等值$\theta$连接和自然连接的差别等。