线段树入门讲解+模板（单点查询/更新、区间查询/更新）

先上模板：

#include
using namespace std;

struct node
{
    int l,r,w,lazy;//tree的l,r表示数组区间[l,r],w表示[l,r]区间和 
}tree[400001];

//lazy!=0是加值,lazy!=-1是改值 

void build(int v,int l,int r)//建树,v表示tree里第v个结点,tree是完全二叉树 
{
    tree[v].l=l;
	tree[v].r=r;
    if(tree[v].l==tree[v].r)
    {
        scanf("%d",&tree[v].w); 
        return;
    }
    int mid=(l+r)/2;
    build(v*2,l,mid);
    build(v*2+1,mid+1,r);
    tree[v].w=tree[v*2].w+tree[v*2+1].w;
}

void downadd(int v)//区间加值lazy=0 标记下传
{
    tree[v*2].lazy+=tree[v].lazy;
    tree[v*2+1].lazy+=tree[v].lazy;
    tree[v*2].w+=tree[v].lazy*(tree[v*2].r-tree[v*2].l+1);
    tree[v*2+1].w+=tree[v].lazy*(tree[v*2+1].r-tree[v*2+1].l+1);
    tree[v].lazy=0;
}

void downupdate(int v)//区间改值lazy=-1 标记下传 
{
    tree[v*2].lazy=tree[v].lazy;
    tree[v*2+1].lazy=tree[v].lazy;
    tree[v*2].w=tree[v].lazy*(tree[v*2].r-tree[v*2].l+1);
    tree[v*2+1].w=tree[v].lazy*(tree[v*2+1].r-tree[v*2+1].l+1);
    tree[v].lazy=-1;
}


int ask_point(int v,int x)//单点查询
{
    if(tree[v].l==tree[v].r)
    {
        return tree[v].w;
    }
    
    if(tree[v].lazy!=0) downadd(v);
    //if(tree[v].lazy!=-1) downupdate(v);//区间改值用-1 
    
    int mid=(tree[v].l+tree[v].r)/2;
    if(x<=mid) ask_point(v*2,x);
    else ask_point(v*2+1,x);
}

void change_point(int v,int x,int y)//单点修改,a[x]改为y(或加减等操作) 
{
    if(tree[v].l==tree[v].r)
    {
        //tree[k].w+=y;
        tree[v].w=y; //找到了x这个点,a[x]=y,也可进行其他操作 
        return;
    }
    if(tree[v].lazy!=0) downadd(v);
    //if(tree[v].lazy!=-1) downupdate(v);//区间改值用-1 
    
    int mid=(tree[v].l+tree[v].r)/2;
    if(x<=mid) change_point(v*2,x,y);
    else change_point(v*2+1,x,y);
    
    tree[v].w=tree[v*2].w+tree[v*2+1].w; 
}

int ask_interval(int v,int a,int b)//区间查询[a,b]
{
    if(tree[v].l>=a&&tree[v].r<=b) 
    {
        return tree[v].w;
    }
    
    if(tree[v].lazy!=0) downadd(v);
    //if(tree[v].lazy!=-1) downupdate(v);//区间改值用-1 
    
    int sum=0;
    int mid=(tree[v].l+tree[v].r)/2;
    if(a<=mid) sum+=ask_interval(v*2,a,b);
    if(b>mid) sum+=ask_interval(v*2+1,a,b);
    
    return sum;
}

void changeadd_interval(int v,int a,int b,int y)//区间加值,[a,b]内所有数同时+y 
{
    if(tree[v].l>=a&&tree[v].r<=b)
    {
        tree[v].w+=(tree[v].r-tree[v].l+1)*y;
        tree[v].lazy+=y;
        return;
    }
    if(tree[v].lazy!=0) downadd(v);
    //if(tree[v].lazy!=-1) downupdate(v);//区间改值用-1 
    
    int mid=(tree[v].l+tree[v].r)/2;
    if(a<=mid) changeadd_interval(v*2,a,b,y);
    if(b>mid) changeadd_interval(v*2+1,a,b,y);
    
    tree[v].w=tree[v*2].w+tree[v*2+1].w;
}

void changeupdate_interval(int v,int a,int b,int y)//区间改值,[a,b]内所有数同时修改为y 
{
    if(tree[v].l>=a&&tree[v].r<=b)
    {
        tree[v].w=(tree[v].r-tree[v].l+1)*y;
        tree[v].lazy=y;
        return;
    }
    if(tree[v].lazy!=0) downadd(v);
    //if(tree[v].lazy!=-1) downupdate(v);//区间改值用-1 
    
    int mid=(tree[v].l+tree[v].r)/2;
    if(a<=mid) changeupdate_interval(v*2,a,b,y);
    if(b>mid) changeupdate_interval(v*2+1,a,b,y);
    
    tree[v].w=tree[v*2].w+tree[v*2+1].w;
}

int main()
{
	int t,n,m;
	scanf("%d",&t);
	while(t--)
	{
		memset(tree,0,sizeof(tree));//除改值其他操作用0 
		//memset(tree,-1,sizeof(tree));//区间改值用-1 
		scanf("%d",&n);//n个节点 
	    build(1,1,n);//建树 
	    scanf("%d",&m);//m种操作 
	    for(int i=1;i<=m;i++)
	    {
	    	int p,x,y,a,b;
	        scanf("%d",&p);
	        if(p==1)
	        {
	        	printf("**************单点查询操作**************\n");
	            scanf("%d",&x);
	            printf("%d\n",ask_point(1,x));//单点查询,输出第x个数 
	        } 
	        else if(p==2)
	        {
				printf("**************单点修改操作**************\n");
	            scanf("%d%d",&x,&y);
	            change_point(1,x,y);//单点修改 
	        }
	        else if(p==3)
	        {
	        	printf("**************区间查询操作**************\n");
	            scanf("%d%d\n",&a,&b);//区间查询 
	            printf("%d\n",ask_interval(1,a,b));//从第1个结点开始查[a,b]区间 
	        }
	        else if(p==4)
	        {
	        	printf("**************区间加值操作**************\n");
	            scanf("%d%d%d",&a,&b,&y);//区间加值,[a,b]都加上y 
	            changeadd_interval(1,a,b,y);
	        }
	        else
	        {
	        	printf("**************区间改值操作**************");
	        	scanf("%d%d%d",&a,&b,&y);//区间改制,[a,b]的值都改为y
				changeupdate_interval(1,a,b,y);
			}
	    }
	}
    return 0;
}

该模板经几次修改与完善，可以处理大部分需要使用线段树操作的简单问题了。

（离散化、扫描线等慢慢补充）

 

 

#include

#define MAX_LEN 1000//开顶点数量n的四倍大小

void build_tree(int arr[],int tree[],int node,int start,int end)//建树 
{
	if(start==end)//递归出口设置好 
	{
		tree[node]=arr[start];//arr[end]
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		
		build_tree(arr,tree,left_node,start,mid);
		build_tree(arr,tree,right_node,mid+1,end);
		tree[node]=tree[left_node]+tree[right_node];
	}
}

void update_tree(int arr[],int tree[],int node,int start,int end,int idx,int val)//单点更新:将arr[idx]的值更新为val 
{
	if(start==end)//递归出口设置好 
	{
		arr[idx]=val;//数组真实值 
		tree[node]=val;//建立的线段树上的值 
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		if(idx>=start&&idx<=mid)
		{
			update_tree(arr,tree,left_node,start,mid,idx,val);
		}
		else
		{
			update_tree(arr,tree,right_node,mid+1,end,idx,val);
		}
		tree[node]=tree[left_node]+tree[right_node];
	}
}

int query_tree(int arr[],int tree[],int node,int start,int end,int L,int R)//区间查询:查询arr[L]到arr[R]的区间和 
{
	/*
	printf("start = %d\n",start);
	printf("end   = %d\n",end);
	printf("\n");
	*/ 
	
	if(Rend)//递归出口设置好 
	{
		return 0;
	}
	else if(L<=start&&end>=R)//注意这个出口 
	{
		return tree[node];
	}
	else if(start==end)
	{
		return tree[node];
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		int sum_left=query_tree(arr,tree,left_node,start,mid,L,R);
		int sum_right=query_tree(arr,tree,right_node,mid+1,end,L,R);
		return sum_left+sum_right;
	}
}

int main()
{
	int arr[]={1,3,5,7,9,11}; 
	int size=6;
	int tree[MAX_LEN]={0};//存线段树 不要忘记清零,把虚点设为0补为完全二叉树 
	
	build_tree(arr,tree,0,0,size-1);
	for(int i=0;i<15;i++)//查看树中的点 
	{
		printf("tree[%d]===%d\n",i,tree[i]);
	}
	printf("\n");

	
	printf("***********************\n");


	update_tree(arr,tree,0,0,size-1,4,6);
	for(int i=0;i<15;i++)//查看树中的点 
	{
		printf("tree[%d]===%d\n",i,tree[i]);
	}
	printf("\n");


	printf("***********************\n");
	

	int s=query_tree(arr,tree,0,0,size-1,2,5);
	printf("s===%d\n",s);	//输出查询的区间和 
	
	
	printf("***********************\n");
	return 0;
}

 

 

 

 

 

 

 

简单讲解:

为了解决在一个区间上 查询区间和 和 修改某一项的值  这些操作，我们使用线段树将复杂度降为O(logn)。

给出一个数组

建好的线段树是这样的：

 

线段树构建：

从图中可以看到，我们是不断将区间分半分半直到区间中只有一个叶子结点，此时我们就得到了这个数组的线段树表示。

在处理的时候我们将该线段树看作完全二叉树（这么说好像并不严谨），将不满的二叉树补上“虚点”补成完全二叉树的形式，其中“虚点”的值为0（这里就需要我们在初始时对存线段树的数组清零），然后每个结点按图中的顺序标号。

（不要把区间和完全二叉树的序号搞混，一个是数组本身的序号，一个是我们建好的树的序号）

这时我们可以就可以使用一个tree数组来存这个线段树了。

 

变量不要搞混：

left_node,right_node等node是表示线段树中的变量

start,end,L,R等是表示数组的值的变量

代码：

void build_tree(int arr[],int tree[],int node,int start,int end)//建树 
{
	if(start==end)//递归出口设置好 
	{
		tree[node]=arr[start];//arr[end]
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		
		build_tree(arr,tree,left_node,start,mid);
		build_tree(arr,tree,right_node,mid+1,end);
		tree[node]=tree[left_node]+tree[right_node];
	}
}

 

线段树单点更新: 

给出指定的数组的下标，我们就可以递归找到这个数在线段树中的位置，然后更新。

更新后对这条路径上所有点产生了影响，所以我们需要更新这些点。

更新线段树tree数组中的值同时也不要忘记更新原数组arr数组中的值

代码：

void update_tree(int arr[],int tree[],int node,int start,int end,int idx,int val)//单点更新:将arr[idx]的值更新为val 
{
	if(start==end)//递归出口设置好 
	{
		arr[idx]=val;//数组真实值 
		tree[node]=val;//建立的线段树上的值 
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		if(idx>=start&&idx<=mid)
		{
			update_tree(arr,tree,left_node,start,mid,idx,val);
		}
		else
		{
			update_tree(arr,tree,right_node,mid+1,end,idx,val);
		}
		tree[node]=tree[left_node]+tree[right_node];
	}
}

 

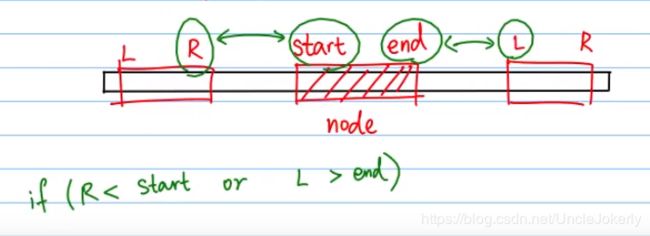
线段树区间查询：

 查询过程与更新过程类似，都是递归在线段树中找出所要查询的区间（单点更新查询到的区间只有一个叶子结点即是找到了）

我们将所要查找的区间统一都分为左半部分和右半部分，左半部分在线段树的左子树找，右半部分在右子树找，然后将两部分的和加起来即为总区间的和。

但是应该考虑几种情况：

1.当前所查区间没有在这个（子）树中，则直接返回0（如果我们要查询[4,5]区间，[4,5]区间没有在左子树不需要再找左子树）

2.和描述一样时，可以分为左右两部分进行查找

3.当找到一个叶子结点时直接返回该叶子结点的值

4.递归到某一子树是完全包含在所查区间的，则直接返回根结点的值（如果没有这个条件会一直递归到这个树的叶子结点，多做无用功）

代码：
 

int query_tree(int arr[],int tree[],int node,int start,int end,int L,int R)//区间查询:查询arr[L]到arr[R]的区间和 
{
	/*
	printf("start = %d\n",start);
	printf("end   = %d\n",end);
	printf("\n");
	*/ 
	
	if(Rend)//递归出口设置好 
	{
		return 0;
	}
	else if(L<=start&&end>=R)//注意这个出口 
	{
		return tree[node];
	}
	else if(start==end)
	{
		return tree[node];
	}
	else
	{
		int mid=(start+end)/2;
		int left_node =2*node+1;
		int right_node=2*node+2;
		int sum_left=query_tree(arr,tree,left_node,start,mid,L,R);
		int sum_right=query_tree(arr,tree,right_node,mid+1,end,L,R);
		return sum_left+sum_right;
	}
}

 

区间更新：（留坑）

思想是查询时先不更新，设置一个lazy数组，待下次查询或更新操作时再往下更新。

 

---

（我来填坑了）

lazy保存在每棵树的根结点信息里,
为了告诉这个树所代表的区间要修改的信息是什么(同时加或减的数是多少),
如果找到了被需要修改的区间完全包含的一棵树(一个区间)或一个叶子结点时,
则更新这棵树的根结点的lazy和根结点的值(值就等于这个这棵树所代表的区间长度*要加的值y--因为区间里的每个数都要加y),
暂时先不更新这个区间的值, 
等到下次执行查询或者再次修改操作时先下放lazy中的值,将每个经历的树的子树(或叶子结点)更新 
加入lazy标记就不用每次递归到叶子结点修改所有的叶子结点了,
只需修改一个被所要修改的区间完全包含的树的根结点的信息即可,每次用到的时候再往下递归 

 

其实说是讲解不如说是总结，与真正的老师之间还存在很大的差距，如果感觉还是很困惑可以听一下这位老师讲的，这篇文章也是总结于此：【数据结构】线段树（Segment Tree）

（疯狂迷恋灯笼大大）

 

 

 

PS:

问：tree数组为什么开4*n+1大小呢？

答：

如图：

当我们n为6时，如果是满二叉树，所有叶子结点（图中的1，2，3，4，5，6）都在同一层，我们需要2n-1就够了，

但是实际上很多情况都是像图中所示的，我们就需要多于2n个结点，开到4n才合适。

这里是证明过程：线段树需要开4倍区间大小的数组的原因

如上述代码所示，我们在写线段树的模板时，别人会告诉我们开4倍的数组就不会溢出了，然而原因是什么，现在证明一下
首先线段树是一棵二叉树，最底层有n个叶子节点（n为区间大小）

那么由此可知，此二叉树的高度为,可证

然后通过等比数列求和求得二叉树的节点个数，具体公式为，（x为树的层数，为树的高度+1）

化简可得,整理之后即为（近似计算忽略掉-1）

证毕