马尔科夫链蒙特卡洛（MCMC） -- 学习笔记

0、前言

蒙特卡罗方法(Monte Carlo Simulation)是一种随机模拟(或者统计模拟)方法。给定一个概率分布p(x)，如何让计算机生成满足这个概率分布的样本。 这个问题就是统计模拟中研究的重要问题–采样(Sampling)。
MCMC(Markov Chain Monte Carlo)算法是其中一种重要的采样方法。

1、马尔科夫链、马尔科夫稳态

马尔科夫链的数学定义如下:
P(Xt+1=x|Xt,Xt−1,…)=P(Xt+1=x|Xt)
状态转移的概率只依赖于前一个状态。

引入一个典例：
给定初始概率转移矩阵（PS：行坐标表示各当前状态，列坐标表示各下一个状态）：

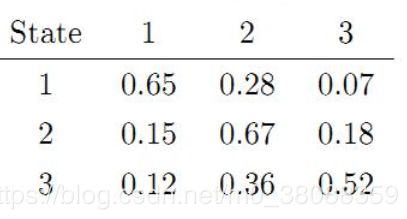
解释：拿第一行来讲，（1,1）位置表示处在第一个状态时转移到第一个状态概率P11=0.65，（1,2）位置表示处在第一个状态转移到第二个状态概率P12=0.28，（1,3）位置表示处在第一个状态转移到第三个状态概率P13=0.07，其他各行同理。

假设初始概率分布为π0=[0.21,0.68,0.11]，也即当前处在各个状态的概率。计算转移前n词的分布状况如下：
（PS：实际就是矩阵相乘，公式为πn=π0Pn，Pn表示转移概率矩阵的第n列概率）

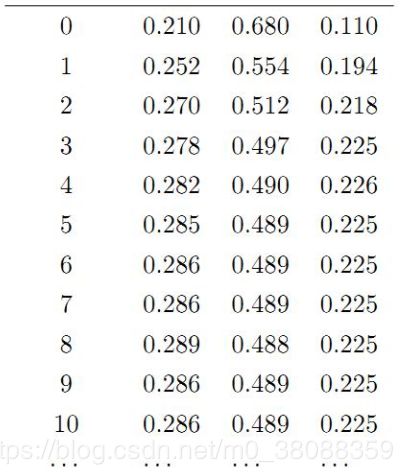
我们发现转移到第七次开始，这个分布就稳定不变了。我们换一个初始概率分布π0=[0.75,0.15,0.1]接着试试看：

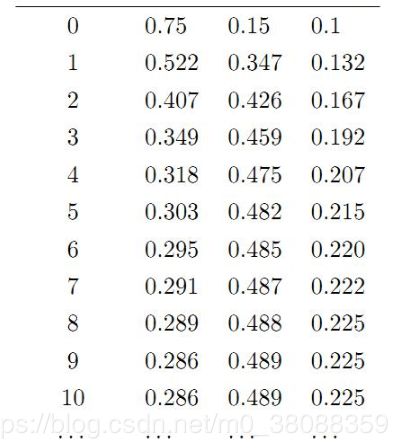
发现两次给定不同的初始概率分布，最终都收敛到概率分布 π=[0.286,0.489,0.225]，也就是说收敛的行为和初始概率分布 π0 无关。这说明这个收敛行为主要是由概率转移矩阵P决定的。
这个收敛现象并非是我们这个马氏链独有的，而是绝大多数马氏链的共同行为。

关于马尔科夫链收敛，有一下定理：

定理中需要说明的地方如下：

2、Markov Chain Monte Carlo

由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,， 如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1⋯。

这个绝妙的想法在1953年被 Metropolis想到了，为了研究粒子系统的平稳性质， Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法，即Metropolis算法，并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法。

MCMC 算法是 Metropolis 算法的一个改进变种，即常用的 Metropolis-Hastings 算法。

马氏链的收敛性质主要由转移矩阵P 决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵P,使得平稳分布恰好是我们要的分布p(x)。

经过对上述MCMC采样算法中接受率的改造，我们就得到了最常见的Metropolis-Hastings算法：

3、Gibbs Sampling

对于高维的情形，由于接受率 α的存在(通常 α<1), 以上 Metropolis-Hastings 算法的效率不够高。
二维情况p(x1,y1)p(y2|x1)=p(x1,y2)p(y1|x1)，任何两个点之间的转移满足细致平稳条件。

推广到高维，如果x1 变为多维情形x1，可以看出推导过程不变，所以细致平稳条件同样是成立的。

p(x1,y1)p(y2|x1)=p(x1,y2)p(y1|x1)

此时转移矩阵 Q 由条件分布 p(y|x1) 定义。上式只是说明了一根坐标轴的情形，和二维情形类似，很容易验证对所有坐标轴都有类似的结论。所以n维空间中对于概率分布 p(x1,x2,⋯,xn) 可以如下定义转移矩阵

如果当前状态为(x1,x2,⋯,xn)，马氏链转移的过程中，只能沿着坐标轴做转移。沿着 xi 这根坐标轴做转移的时候，转移概率由条件概率 p(xi|x1,⋯,xi−1,xi+1,⋯,xn) 定义；
其它无法沿着单根坐标轴进行的跳转，转移概率都设置为 0。
于是我们可以把Gibbs Smapling 算法从采样二维的 p(x,y) 推广到采样n 维的 p(x1,x2,⋯,xn)：

以上算法收敛后，得到的就是概率分布p(x1,x2,⋯,xn)的样本，当然这些样本并不独立，但是我们此处要求的是采样得到的样本符合给定的概率分布，并不要求独立。

在以上算法中，坐标轴轮换采样不是必须的，可以在坐标轴轮换中引入随机性，这时候转移矩阵 Q 中任何两个点的转移概率中就会包含坐标轴选择的概率，而在通常的 Gibbs Sampling 算法中，坐标轴轮换是一个确定性的过程，也就是在给定时刻t，在一根固定的坐标轴上转移的概率是1。

参考学习自：
https://www.cnblogs.com/Erdos001/p/4749069.html