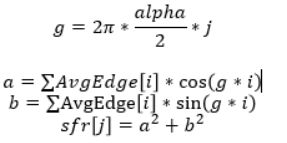SFR 原理分析 代码
MTF:REF
在表示相机图像解析力时,通常采用MTF50或者MTF50P。
MTF50是当MTF数值下降至最大值的50%时,对应的频率(Cycle Per Pixel),它是一个广泛应用的锐利度衡量标准。但是它有一个重大的缺陷,就是当影像模组内部的软件对影像作锐利化时,对MTF数值有很大的影响,而其实大部分模组都会对影像作不同程度的锐利化,这就导致了MTF50已经不能够正确的反映锐利度的数值了。
由于前面所述原因,MTF50P被应用在锐利度的评价当中。MTF50P是使影像过度锐化以后再计算MTF数值,其MTF数值的最大值的50%对应的频率值。
SFR(spatial frequency response)表示空间频率响应,表示的也是相机的解像能力,在这个层面上,MTF与SFR是一样的意思。
SFR(spatial frequency response ) 主要用于测量随着空间频率的线条增加对单一影像所造成的影响。简言之SFR就是MTF的另外一种测试方法。这种测试方法在很大程度上精简了测试流程。SFR的计算目标是获得MTF曲线。SFR的计算方法和MTF虽然不同但是在结果上是一致的。
SFR不需要拍摄不同的空间频率下的线对。它只需要一个黑白的斜边(刀口)即可换算出约略相等于所有空间频率 下的MTF。
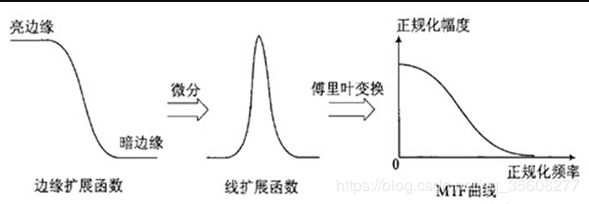
SFR是通过这条斜边的图进行超采样的到一条更加细腻的黑白变换的直线(ESF)。然后通过这条直线求导得到直线的变化率(LSF)。然后对将这个变化率进行FFT变换就能得到各个频率下的MTF的值。这里面的ESF,LSF,都是什么呢?
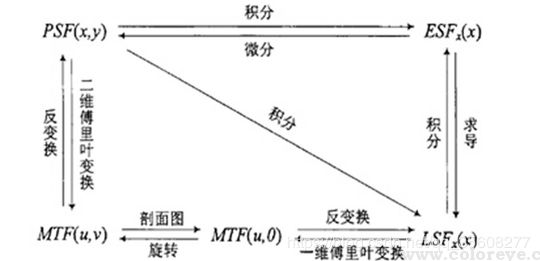
点扩展函数PSF(Point Spread Function)、线扩展函数LSF(Line Spread Function)和边缘扩展函数ESF(Edge Spread Function)是SFR 计算中的几个重要的概念。点扩展函数PSF是点光源成像后的亮度分布函数,如下图所示,
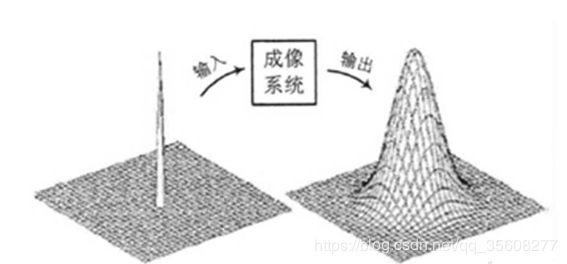
用PSF(X,Y)表示。点扩展函数是中心圆对称的,通常以沿x轴的亮度分布PSF(X,Y)作为成像系统的点扩展函数。
当获取点光源像的亮度分布函数PSF(X,Y)后,对其进行二维傅里叶变换即可得MTF (u,v)。因此,从理论上讲,从PSF也是获取MTF的一个方法。但是,在实际的应用中,由于地面点光源强度很弱,此方法一般较少采用。
相对于PSF来说,LSF的能量得到了一定程度的加强。
SFR计算MTF(通过斜边) 就是通过ESF来得到LSF,然后进行FFT得到MTF各个频率的值的。这几者之间的关系如下图。
https://blog.csdn.net/u011961033/article/details/103136186?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
https://blog.csdn.net/weixin_30911451/article/details/97913237
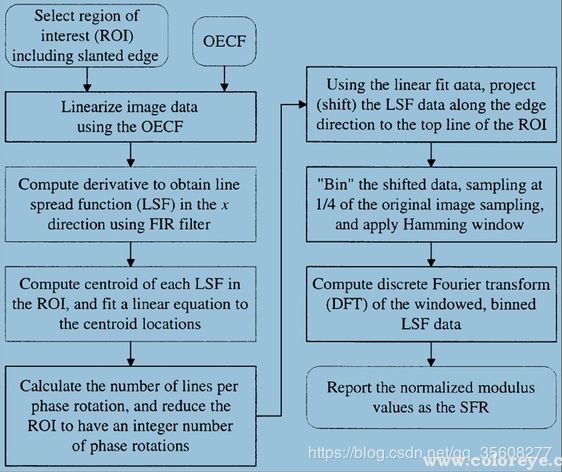
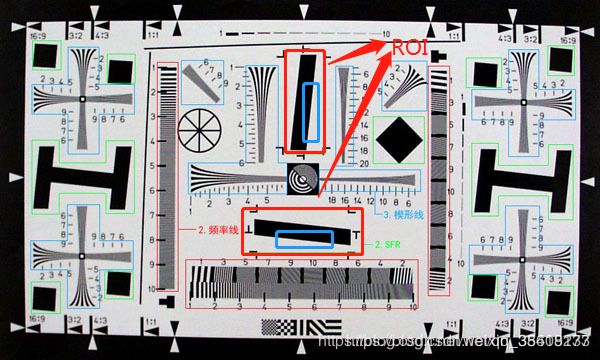
0、获取垂直斜边的ROI
1、进行数据的归一化
2、计算图像每一行的像素矩心
3、对每行的矩心使用最小二乘法进行线性拟合,获得一条关于矩心的直线
4、重新定位ROI,获得ESF
5、对获得的ESF进行四倍超采样
6、通过差分运算获得LSF
7、对LSF应用汉明窗
8、进行DFT运算
0 获取垂直边缘的ROI:

![]()
这里水平和垂直的Edge只是为了计算图像在水平方向和垂直方向的解析力,与算法本身无关,因为水平的Edge会被进行90°旋转后作为输入,然后计算SFR的值
1、进行数据的归一化
在Sensor获得图像之后,呈现出来的图像由于要符合人眼的感觉,会对图像像素进行伽马变换,使得其变成非线性的像素数据,从而使图像的显示更加符合人眼的感受。所以,当我们要进行sensor的成像解析力分析时,要先将图像处理成没有经过伽马变换前的。
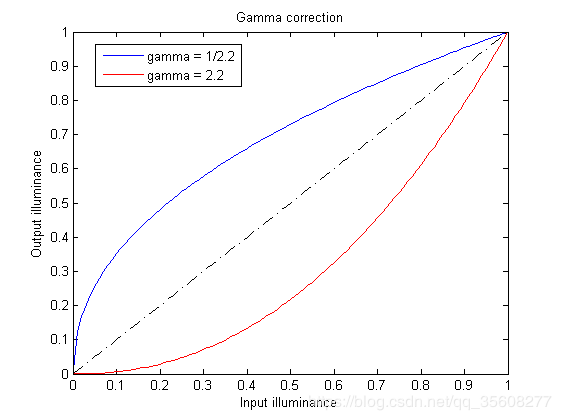
一般sensor会对raw图像进行一个2.2的gamma变换,若我们想恢复原始图像时,我们只需要进行一个1/2.2的gamma变换即可。
2、计算图像每一行的像素矩心
这一步的操作其实是为了计算出边缘的位置。具体讲来就是,我们会将图片中的每一行像素都计算具体的矩心位置。
可以看到,其实每一行像素的矩心计算出来的结果,其实就是在黑白分界线的附近。

矩心的计算公式如下:
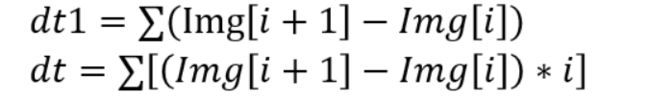
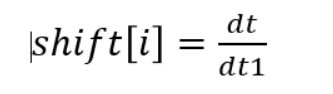
shift[i]就是对应的第i行的矩心位置。
/*****************************************************************************/
unsigned short locate_centroids(double *farea, double *temp,
double *shifts,
unsigned short size_x, unsigned short size_y,
double *offset) {
unsigned long i, j;
double dt, dt1, dt2;
/* Compute the first difference on each line. Interpolate to find the
centroid of the first derivatives. */
for (j = 0; j < size_y; j++) {
dt = 0.0;
dt1 = 0.0;
for (i = 0; i < size_x-1; i++) {
dt2 = farea[(j*(long)size_x)+(i+1)] - farea[(j*(long)size_x)+i];
dt += dt2 * (double)i;
dt1 += dt2;
}
shifts[j]=dt/dt1;
}
/* check again to be sure we aren't too close to an edge on the corners.
If the black to white transition is closer than 2 pixels from either
side of the data box, return an error of 5; the calling program will
display an error message (the same one as if there were not a difference
between the left and right sides of the box ) */
if (shifts[size_y-1] < 2 || size_x - shifts[size_y-1] < 2) {
fprintf(stderr,"** WARNING: Edge comes too close to the ROI corners.\n");
return 5;
}
//防止矩心过于靠近图像的边界
if (shifts[0] < 2 || size_x - shifts[0] < 2){
fprintf(stderr,"** WARNING: Edge comes too close to the ROI corners.\n");
return 5;
}
/* Reference rows to the vertical centre of the data box */
j = size_y/2;
dt = shifts[j];
for (i = 0; i < size_y; i++) {
temp[i] = (double)i - (double)j;
shifts[i] -= dt;
}
*offset = dt;
return 0;
}
3、对每行的矩心使用最小二乘法进行线性拟合,获得一条关于矩心的直线
我们知道用的是最小二乘法就可以了。最小二乘法公式如下:
unsigned short fit(unsigned long ndata, double *x, double *y, double *b,
double *a, double *R2, double *avar, double *bvar)
{
unsigned long i;
double t,sxoss,syoss,sx=0.0,sy=0.0,st2=0.0;
double ss,sst,sigdat,chi2,siga,sigb;
*b=0.0;
for ( i=0; i < ndata; i++ ) {
sx += x[i];//x的叠加
sy += y[i];//y的叠加
}
//求平均值
ss=(double)ndata;
sxoss=sx/ss;
syoss=sy/ss;
for ( i=0; i < ndata; i++ ) {
t = x[i] - sxoss; //
st2 += t*t; //方差
*b += t * y[i];
}
*b /= st2; /* slope *///斜率
*a =(sy-sx*(*b))/ss; /* intercept *///截距
siga=sqrt((1.0+sx*sx/(ss*st2))/ss);
sigb=sqrt(1.0/st2);
chi2=0.0;
sst=0.0;
for (i=0; i < ndata; i++) {
chi2 += SQR( y[i] - (*a) - (*b) * x[i]);
sst += SQR( y[i] - syoss);
}
sigdat=sqrt(chi2/(ndata-2));
siga *= sigdat;
sigb *= sigdat;
*R2 = 1.0 - chi2/sst;//拟合程度
*avar = siga;
*bvar = sigb;
return 0;
}
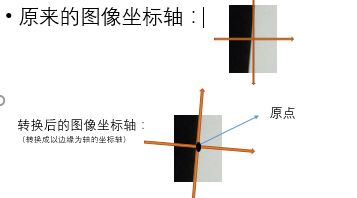
4、重新定位ROI,获得ESF
首先,转换坐标轴,将坐标轴转换到计算出来的矩心直线上。如图所示:
/* Start image at new location, so that same row is center */
center_row = *nrows/2;
start_row = center_row - size_y/2;
farea_old = farea;
farea = farea + start_row*size_x;
/* On center row how much shift to get edge centered in row. */
/* offset = 0.; Original code effectively used this (no centering)*/
if(user_angle)
offset = *off - size_x/2;
else
offset = offset1 + 0.5 + offset2 - size_x/2;
*off = offset;
if(version & ROUND || version & DER3)
offset += 0.125;
if (err != 0) { /* Slopes are bad. But send back enough
data, so a diagnostic image has a chance. */
*pcnt2 = 2*size_x; /* Ignore derivative peak */
return 4;
}
/* reference the temp and shifts values to the new y centre */
/* Instead of using the values in shifts, synthesize new ones based on
the best fit line. */
col = size_y/2;
for (i=0; i < size_y; i++) {
shifts[i] = (*slope) * (double)(i-col) + offset;
}
5、对获得的ESF进行四倍超采样
然后,我们将每一行中X轴坐标相等的像素值累加起来,然后求均值后得到下面第一行的数组。
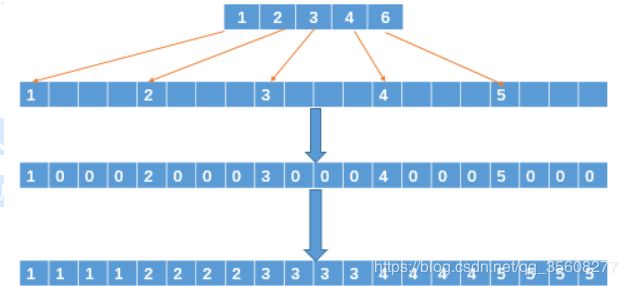
这里是将整张图片的像素转换为一个长度为rows的数组,然后进行4倍的扩增。然后其他没有像素的地方,是进行一个向前寻找非0的像素值进行替换,这样就获得了ESF。
//进行超采样,生成长度为size_x*ALPHA(4)的当行图像(ESF),保存在AveEdge中
unsigned short bin_to_regular_xgrid(unsigned short alpha,//alpha->指的是超取样的倍数
double *edgex, double *Signal,
double *AveEdge, long *counts,
unsigned short size_x,
unsigned short size_y)
{
long i, j, k,bin_number;
long bin_len;
int nzeros;
bin_len = size_x * alpha; //扩大四倍
for (i=0; i<bin_len; i++) {
AveEdge[i] = 0;
counts[i] = 0;
}
for (i=0; i<(size_x*(long)size_y); i++) {
bin_number = (long)floor((double)alpha*edgex[i]);//向下取整
if (bin_number >= 0) {
if (bin_number <= (bin_len - 1) ) {
AveEdge[bin_number] = AveEdge[bin_number] + Signal[i];//把每一行的距离边缘x轴一样远的信号相加
counts[bin_number] = (counts[bin_number])+1;//记录下对应位置有多少个信号相加
}
}
}
nzeros = 0;
for (i=0; i<bin_len; i++) {
j = 0;
k = 1;
//感觉写的有点复杂
if (counts[i] == 0) {
nzeros++; //记录有多少个位置是空的,即没有信号
//K的作用:因为这里的信号为0,找到后面第一个不为零的值,赋给当前这个零
if (i == 0) {
while (!j) { //当j==0时,表示此处的信号为0
if (counts[i+k] != 0) {//第一行的元素
AveEdge[i] = AveEdge[i+k]/((double) counts[i+k]);
j = 1;//充当flag。。。为啥不用布尔类型
}
else k++;//直到找到第一个不为零的数字才会停止
}
} else {
while (!j && ((i-k) >= 0) ) { //j==0&&i-k>=0 j==0说明 counts[i]是0 i-k>0说明 k在i前面,找前面不为零的数值赋给AveEdge[i]
if ( counts[i-k] != 0) {
AveEdge[i] = AveEdge[i-k]; /* Don't divide by counts since it already happened in previous iteration */
j = 1;
}
else k++;
}
if ( (i-k) < 0 ) {//k>i,其实联合上面那段,就是:此处的counts[i]累加次数为零,所以AveEdge[i]也就是0,所以要找到附近一个不为零的值赋给AveEdge[i]
k = 1;
while (!j) {
if (counts[i+k] != 0) {
AveEdge[i] = AveEdge[i+k]/((double) counts[i+k]);
j = 1;
}
else k++;
}
}
}
}
else
AveEdge[i] = (AveEdge[i])/ ((double) counts[i]);//如果此处不为零,直接就求个平均值
}
if (nzeros > 0) {//提示信息
fprintf(stderr, "\nWARNING: %d Zero counts found during projection binning.\n", nzeros);
fprintf(stderr, "The edge angle may be large, or you may need more lines of data.\n\n");
}
return nzeros;
}
6、通过差分运算获得LSF
得到的ESF数组元素进行差分,获得LSF。一下是函数公式:
void calculate_derivative(unsigned int len, double *AveTmp, double *AveEdge,
double *centroid,int separation)
{
unsigned long i;
double dt, dt1;
dt = 0.0;
dt1 = 0.0;
for (i=0; i< len; i++)
AveTmp[i] = AveEdge[i];
for (i=1; i< len-separation; i++) {
/* Not wasting time with division by 2 since constant factors don't
change SFR computation */
AveEdge[i] = (AveTmp[i+separation]-AveTmp[i-1]);
if (separation == 1)
AveEdge[i] /= 2.0;
dt += AveEdge[i] * (double)i;
dt1 += AveEdge[i];
}
*centroid = dt/dt1;
AveEdge[0] = AveEdge[1];
if (separation == 1) AveEdge[len-1] = AveEdge[len-2];
}
7、对LSF应用汉明窗
对上面的LSF数组进行汉明窗处理,这一步主要也是看公式,如下:
void apply_hamming_window( unsigned short alpha,
unsigned int oldlen, //size_x*4
unsigned short newxwidth, //size_x
double *AveEdge, long *pcnt2)
{
long i,j,k, begin, end, edge_offset;
double sfrc;
/* Shift the AvgEdge[i] vector to centre the lsf in the transform window */
// 将Avgedge移到中心位置, 两边由于移动造成的空位由0补齐
edge_offset = (*pcnt2) - (oldlen/2);//不能理解为什么一定要反着计算,pcnt2肯定是小于oldlen/2吧。。
if (edge_offset != 0) { //cer=6
if (edge_offset < 0 ) { //这里根据分析的话,应该edge_offset只会小于0啊。。 ↓
for (i=oldlen-1; i > -edge_offset-1; i--) // [l l l l l l l max l l l l l]
AveEdge[i] = (AveEdge[i+edge_offset]); // ↑ ↑ ↑
for (i=0; i < -edge_offset; i++) // left center=3 right
AveEdge[i] = 0.00; /* last operation */ //offset = center-cer=-3
} else { // cer=6
// ↓
for (i=0; i < oldlen-edge_offset; i++) // [0 0 0 l l l l l l l max l l]
AveEdge[i] = (AveEdge[i+edge_offset]); // ↑ ↑ ↑
for (i=oldlen-edge_offset; i < oldlen; i++) // center=3
AveEdge[i] = 0.00;
}
}
/* Multiply the LSF data by a Hamming window of width NEWXWIDTH*alpha */
//将begin和end两侧的值用0填充,但是感觉没啥用
begin = (oldlen/2)-(newxwidth*alpha/2);//上下看来,begin只会等于0,因为oldlen=bin_len, bin_len=size_x*alpha == newxwidth*alpha
if (begin < 0) begin = 0;
end = (oldlen/2)+(newxwidth*alpha/2);
if (end > oldlen ) end = oldlen;
for (i=0; i< begin; i++)
AveEdge[i] = 0.0;
for (i=end; i< oldlen; i++)
AveEdge[i] = 0.0;
// 给begin和end之间的数据加上汉明窗
// 汉明窗 W(n,α ) = (1 -α ) - α cos(2*PI*n/(N-1)) ,(0≤n≤N-1)
// 一般情况下,α取0.46
// 下面计算方法等于窗发生了平移(故符号发生了变化), 结果是一样的
for (i=begin,j = -newxwidth*alpha/2; i < end; i++,j++) {
sfrc = 0.54 + 0.46*cos( (M_PI*(double)j)/(newxwidth*alpha/2) );
AveEdge[i] = (AveEdge[i])*sfrc;
}
//将lsfbegin的位置左移到index0的位置
//但在代码中应该是不会起作用的,
if (begin != 0) /* Shift LSF to begin at index 0 (rather than begin) */
for (k=0, i=begin; k<newxwidth*alpha; i++,k++)
AveEdge[k] = AveEdge[i];
}
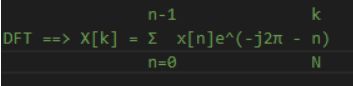
8、进行DFT运算
unsigned short ftwos(long number, double dx, double *lsf,
long ns, double ds, double *sfr)
{
double a, b, twopi, g;
long i,j;
// n-1 k
// DFT ==> X[k] = Σ x[n]e^(-j2π - n)
// n=0 N
twopi = 2.0 * M_PI;
for (j = 0; j < ns; j++){//ns=1/2*bin_len 前一半
g = twopi * dx * ds * (double)j;
for (i = 0, a = 0, b = 0; i < number; i++) {
a += lsf[i] * cos(g * (double)(i));
b += lsf[i] * sin(g * (double)(i));
}
sfr[j] = sqrt(a * a + b * b);
}
return 0;
}
main
short sfrProc (double **freq, double **sfr,
int *len,
double *farea,
unsigned short size_x, int *nrows,
double *slope, int *numcycles, int *pcnt2, double *off, double *R2,
int version, int iterate, int user_angle)
{
unsigned short i, j, col, err = 0;
long pcnt;
double dt, dt1, sfrc, tmp, tmp2;
double *temp=NULL, *shifts=NULL, *edgex=NULL, *Signal=NULL;
double *AveEdge=NULL, *AveTmp=NULL;
long *counts=NULL;
int nzero;
unsigned short size_y;
unsigned int bin_len;
double avar, bvar, offset1, offset2, offset;
double centroid;
int start_row, center_row;
double *farea_old;
double cyclelimit;
FILE *fp = NULL;
size_y = *nrows;
/* Verify input selection dimensions are EVEN */
if (size_x%2 != 0) {
fprintf(stderr, "ROI width is not even. Does this really matter???\n");
return 1;
}
/* At least this many cycles required. */
/* For special iterative versions of the code, it can go lower */
if (iterate) cyclelimit = 1.0;
else cyclelimit = 5.0;
/* Allocate memory */
shifts = (double *)malloc(size_y*sizeof(double));
temp = (double *)malloc(size_y*sizeof(double));
edgex = (double *)malloc(size_y*size_x*sizeof(double));
Signal = (double *)malloc(size_y*size_x*sizeof(double));
if( !user_angle ) {
//定位矩心位置
err = locate_centroids(farea, temp, shifts, size_x, size_y, &offset1);
if (err != 0) { return 2; }
/* Calculate the best fit line to the centroids */
/*计算矩心的拟合曲线*/
err = fit(size_y, temp, shifts, slope, &offset2, R2, &avar, &bvar);
if (err != 0) { return 3; }
if (version)
MTFPRINT4("\nLinear Fit: R2 = %.3f SE_intercept = %.2f SE_angle = %.3f\n",
*R2, avar, atan(bvar)*(double)(180.0/M_PI))
}
/* Check slope is OK, and set size_y to be full multiple of cycles */
//检查刀口斜率,以确保后面超采样的质量
err = check_slope(*slope, &size_y, numcycles, cyclelimit, 1);
/* Start image at new location, so that same row is center */
//调整ROI的行
center_row = *nrows/2;
start_row = center_row - size_y/2;
farea_old = farea;
farea = farea + start_row*size_x;
/* On center row how much shift to get edge centered in row. */
/* offset = 0.; Original code effectively used this (no centering)*/
if(user_angle)
offset = *off - size_x/2;
else
offset = offset1 + 0.5 + offset2 - size_x/2;
*off = offset;
if(version & ROUND || version & DER3)
offset += 0.125;
if (err != 0) { /* Slopes are bad. But send back enough
data, so a diagnostic image has a chance. */
*pcnt2 = 2*size_x; /* Ignore derivative peak */
return 4;
}
/* reference the temp and shifts values to the new y centre */
/* Instead of using the values in shifts, synthesize new ones based on
the best fit line. */
// 基于拟合结果更新shifts
col = size_y/2;
for (i=0; i < size_y; i++) {
shifts[i] = (*slope) * (double)(i-col) + offset;
}
/* Don't normalize the data. It gets normalized during dft process */
//不要对数据进行归一化,数据在DFT处理过程中会被归一化
/* To normalize here, set dt = min and dt1 = max of farea data */
//如果要在这里初始化,将dt设置为最小值,dt1设置为最大值
dt = 0.0;
dt1 = 1.0;
if (version & ESFFILE)
fp = fopen("esf.txt","w");
/* Calculate a long paired list of x values and signal values */
pcnt = 0;
for (j = 0; j < size_y; j++) {
for (i = 0; i < size_x; i++) {
edgex[pcnt] = (double)i - shifts[j];//计算每个点到刀口的距离
Signal[pcnt] = ((farea[((j*(long)size_x)+i)]) - dt)/(dt1-dt); //归一化每个点的亮度
if ((version & ESFFILE) && edgex[pcnt] < size_x/2 + 3 &&
edgex[pcnt] > size_x/2 - 3)
fprintf(fp, "%f %f\n", edgex[pcnt], Signal[pcnt]);
pcnt++;
}
}
if (version & ESFFILE)
fclose(fp);
/* Allocate more memory */
bin_len = (unsigned int)(ALPHA*size_x);
AveEdge = (double *)malloc(bin_len*sizeof(double));
AveTmp = (double *)malloc(bin_len*sizeof(double));
counts = (long *)malloc(bin_len*sizeof(long));
/* Project ESF data into supersampled bins */
//进行超采样,生成长度为size_x*ALPHA(4)的当行图像(ESF),保存在AveEdge中
nzero = bin_to_regular_xgrid((unsigned short)ALPHA, edgex, Signal,
AveEdge, counts,
size_x, size_y);
free(counts);
free(Signal);
free(edgex);
/* Compute LSF from ESF. Not yet centered or windowed. */
// 将ESF转换为差分图LSF, 并计算LSF的矩心
if ( (version&DER3) )
calculate_derivative( bin_len, AveTmp, AveEdge, ¢roid, 1);
else
calculate_derivative( bin_len, AveTmp, AveEdge, ¢roid, 0);
if (iterate == 0) {
/* Copy ESF to output area */
for ( i=0; i<bin_len; i++ )
farea_old[i] = AveTmp[i];
}
/* Find the peak/center of LSF */
//寻找LSF的最大值
locate_max_PSF( bin_len, AveEdge, &pcnt);//这里获得了最大值的中心
free(shifts);
free(temp);
if(version)
MTFPRINT3("Off center distance (1/4 pixel units): Peak %ld Centroid %.2f\n",
pcnt-bin_len/2, centroid-bin_len/2)
if((version & PEAK) == 0)//忽略差分后的最大值
pcnt = bin_len/2; /* Ignore derivative peak */
else
MTFPRINT("Shifting peak to center\n")
/* Here the array length is shortened to ww_in_pixels*ALPHA,
and the LSF peak is centered and Hamming windowed. */
//将LSF的最大值移到中心位置,并加上汉明窗
apply_hamming_window((unsigned short)ALPHA, bin_len,
(unsigned short)size_x,
AveEdge, &pcnt);
/* From now on this is the length used. */
*len = bin_len/2;
if (iterate == 0) {
/* Copy LSF_w to output area */
for ( i=0; i<bin_len; i++ )
farea_old[size_x*(int)ALPHA+i] = AveEdge[i];
}
tmp = 1.0;
tmp2 = 1.0/((double)bin_len) ;
/* Now perform the DFT on AveEdge */
/* ftwos ( nx, dx, lsf(x), nf, df, sfr(f) ) */
//ftwos( number, dx, *lsf, ns, ds, *sfr)
(void) ftwos(bin_len, tmp, AveEdge, (long)(*len),
tmp2, AveTmp);
if(*freq==NULL)
(*freq) = (double *)malloc((*len)*sizeof(double));
if(*sfr==NULL)
(*sfr) = (double *)malloc((*len)*sizeof(double));
for (i=0; i<(*len); i++) {
sfrc = AveTmp[i];
(*freq)[i]= ((double)i/(double)size_x); //每个点对应的频率
(*sfr)[i] = (double) (sfrc/AveTmp[0]); //归一化sfr
}
/* Free */
free(AveEdge);
free(AveTmp);
*nrows = size_y;
*pcnt2 = pcnt;
return(0);
}
ref
https://blog.csdn.net/tanjiaqi2554/article/details/101826860?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase