2018杭电多校第七场

A

01图可以用双端队列快速求出最短路

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
inline char inputchar()
{
    return getchar();
}
inline void inputnum(int &ret)
{
    char ch = inputchar();
    while(ch < '0' || ch > '9')
        ch = inputchar();
    ret = ch - '0';
    ch = inputchar();
    while(ch >= '0' && ch <= '9')
    {
        ret = ret * 10 + ch - '0';
        ch = inputchar();
    }
}
const int MAXN = 101010, MAXM = 202020;
int n, m;
class Edge
{
public:
    int to, c, next;
}e[MAXM * 2];
int en, head[MAXN];
int dis[MAXM];
deque q;
void insert()
{
    int u, v, c;
//    scanf("%d%d%d", &u, &v, &c);
    inputnum(u);
    inputnum(v);
    inputnum(c);
    e[++en].to = v;
    e[en].c = c;
    e[en].next = head[u];
    head[u] = en;
    e[++en].to = u;
    e[en].c = c;
    e[en].next = head[v];
    head[v] = en;
}
bool solve()
{
    if(scanf("%d%d", &n, &m) != 2)
        return false;
    memset(head, -1, (n + 2) * sizeof(int));
    en = 1;
    for(int i = 1; i <= m; i++)
        insert();
    memset(dis, 1, (m + 2) * sizeof(int));
    for(int i = head[1]; i > 0; i = e[i].next)
        dis[i / 2] = 1, q.push_back(i / 2);
    while(!q.empty())
    {
        int now = q.front();
        q.pop_front();
        for(int i = head[e[now * 2].to]; i > 0; i = e[i].next)
            if(e[i].c == e[now * 2].c)
            {
                if(dis[i / 2] > dis[now])
                    dis[i / 2] = dis[now], q.push_front(i / 2);
            }
            else
            {
                if(dis[i / 2] > dis[now] + 1)
                    dis[i / 2] = dis[now] + 1, q.push_back(i / 2);
            }
        for(int i = head[e[now * 2 + 1].to]; i > 0; i = e[i].next)
            if(e[i].c == e[now * 2 + 1].c)
            {
                if(dis[i / 2] > dis[now])
                    dis[i / 2] = dis[now], q.push_front(i / 2);
            }
            else
            {
                if(dis[i / 2] > dis[now] + 1)
                    dis[i / 2] = dis[now] + 1, q.push_back(i / 2);
            }
    }
    int ans = MAXM;
    for(int i = head[n]; i > 0; i = e[i].next)
        if(ans > dis[i / 2])
            ans = dis[i / 2];
    if(ans == MAXM)
        ans = -1;
    printf("%d\n", ans);
    return true;
}
int main()
{
    while(solve());
    return 0;
}

 

J

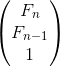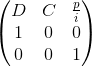
首先要说的就是这题就很打脸了，之前我刚说的矩阵快速幂只有在对付斐波那契数列有用，其实，只要是递推式，都可以用它来解决，只要构造好了矩阵，那么这题的矩阵是什么呢？由这个式子可得=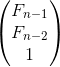，只要进行对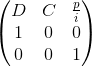的快速幂即可。but，在递推式的最后一项（即floor（p/i））是一个定值的时候才可以这样做，可是它是会变的。于是注意到我们有这样一个结论，在1~n中，floor(p/i)最多只有根号n个不同的数，所以就可以进行分段了——在每一段内是可以快速幂递推的，然后到边界的话暴力去算，怎样确定是否到达边界呢，可以使用二分查找的办法。

#include
using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;
ll A, B, C, D, N, P;
struct mat  {
    ll a[3][3];
}c;
mat mat_mul(mat x, mat y){
    mat s;  
    memset(s. a, 0, sizeof(s. a));
    for(int i = 0; i < 3; i ++)
    for(int j = 0; j < 3; j ++)
    for(int k = 0; k < 3; k ++)
        s. a[i][j] = (s. a[i][j] + x. a[i][k] * y. a[k][j] % mod) % mod;     
    return s;
}
mat mat_pow(ll n){
	mat res;
	memset(res. a, 0, sizeof(res. a));
	res. a[0][0] = res. a[1][1] = res. a[2][2] = 1;
    while(n){
        if(n & 1) 
			res = mat_mul(res, c);  
        c = mat_mul(c, c);  
        n >>= 1;
    }
    return res;
}
ll solove(ll i){
	ll l = i, r = N;
	ll p = P / i;
	while(l < r){
		int mid = r - (r - l) / 2; //防止爆int 
		if(p == P / mid)
			l = mid;
		else if(p > P / mid)
			r = mid - 1;
		else l = mid + 1;
	}
	return l;
}
 
int main(){
	int T;
	scanf("%d", &T);
	while(T --){
		scanf("%lld %lld %lld %lld %lld %lld", &A, &B, &C, &D, &P, &N);
		if(N == 1){
			printf("%lld\n", A);
			continue;
		}
		if(N == 2){
			printf("%lld\n", B);
			continue;
		}
		ll f1 = B;
		ll f2 = A;
		mat ans;
		for(ll i = 3; i <= N;){
			ll j = solove(i);		
			memset(c. a, 0, sizeof(c. a));
			c. a[0][0] = D;
			c. a[0][1] = C;
			c. a[2][2] = 1;
			c. a[1][0] = 1;
			c. a[0][2] = P / i;
			ans = mat_pow(j - i + 1);
			ll ff1 = (ans. a[0][0] * f1 % mod + ans. a[0][1] * f2 % mod + ans. a[0][2]) % mod;
			ll ff2 = (ans. a[1][0] * f1 % mod + ans. a[1][1] * f2 % mod + ans. a[1][2]) % mod;
			f1 = ff1;
			f2 = ff2;
			i = j + 1;
		}
		printf("%lld\n", f1);
	}
    return 0;
}

三项递推，所以写3*3的矩阵，sogasoga（海蜇的碎碎念）