闲聊——集成学习理论（Adaboost，随机森林理论与个人实战中的体会）

（本文通过简单的例子来引出算法本质，同时附上证明过程，目的是让感觉直接看证明推导很难的小伙伴们也能理解集成算法是怎样实现的）
集成学习通过构建并结合多个学习器来完成学习任务，可获得比单一学习器更好的泛化性能。目前的集成学习方法大致可分为两类，第一类个体学习器之间具有很强的依赖关系，需要串行生成的序列化方法；第二类是个体学习器之间不存在强依赖关系，可同时生成的并行化方法。这里分别对两类集成方法各举一个例子。

AdaBoost算法

AdaBoost算法是第一类集成学习算法的一种，我们先通过一个简单的例子来看一下它的原理。
现在有一个二分类任务，它的二维散布图如下：

这里星星和圆圈代表两个类别。我们假设各个样本的权重相同，（即对各样本公平处理），那么以最简单的方法，分错的数量来定义损失函数。那么对于一般的线性分类器，通常会进行这样的分类：

可以看到此时分类器将四个星星判断为圆圈，那么如果我们不希望这些样本被分错，可以给它们更大的权重，例如设置这四个点权重为1.5，（即每分错这四个点中的一个，损失函数增加1.5），那么此时损失函数将变为6，而若如此划分：

那么损失函数就会变成5.5。（分错一个1.5和四个1）
这显然优化了损失函数。但这样划分又将一部分样本进行了错误分类，那么我们再进行一次权重更新。对于此次分错的四个圆圈，我们更新权重为1.5，而两次都分错的星星样本，更新权重为1，那么此时的损失函数值为9（分错四个1.5的圆和一个3的星星），而若做如下划分：

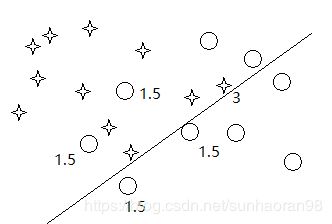
那么损失函数将为5（分错两个1.5的圆和两个1的圆），比9要更小。
可以看出，我们进行的三次划分，分别分错了4，5，4个点，并在更新各样本权重之后优化了新的损失函数。有的小伙伴会有疑问，既然线性分类器第一次就分错的最少，那为什么还要进行下面的操作呢？
单看一个分类器，显然我们所做的一切没有对结果进行优化。而如果我们将这三个分类器进行加权投票（以1，1，1权重举例，两个及以上的分类器确定样本点属于哪一类，我们就认为它属于哪一类），那么可以得到结果如下（涂黑的代表分类正确）：

可以看到只有三个点分类错误，即我们将这三个分类器结合之后，分类效果更好。
我们将这种学习器（这个例子里是分类器）结合，叫做一种集成。而上面介绍的方法，也是Adaboost算法的思想。
后面我们把单个学习器叫做基学习器（又叫弱学习器）。

为了方便不喜欢看数学推导的小伙伴们，这里先给出Adaboost算法的步骤。
我们有训练集D = {(x1,y1),(x2,y2),…,(xm,ym)}
基学习算法η
训练轮数T
样本权值分布A
基学习器h
基学习器权重α
真实函数f(x) （结果为0，1）
过程：（此处At,ht,αt中的t均为脚标）
1：初始化A1(x) = 1/m //首先给各个样本分配同样的权值。
2：for t =1,2,…T Do
3: ht = η(D,At(x)) //基于分布A(t)(x)从数据集D中训练出分类器ht
4： εt = P(ht(x) ≠ f(x))，（在样本权值x服从At的情况下） //估计分类器误差
5： if εt > 0.5 then break //如果基学习器ht分类准确率不足一半，那么我们认为继续集成，准确率不会再升高，于是训练结束
6： αt =1/2 * ln((1- εt)/εt) //确定基学习器权重，至于为什么是这个函数，后面会有证明
7： if ht(x) = f(x)：
8： A(t+1)(x) = (At(x)/Z t) * exp(-αt)
9： if ht(x) = f(x)：
10： A(t+1)(x) = (At(x)/Z t) * exp(αt) //更新样本分布A(t)(x)
11:end for
输出：

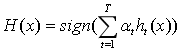
其中H(x)为集成算法，sign(x)为符号函数，括号内x大于0表示分类为1，小于等于0表示分类为-1 （0，1分类也是类似，判断标准为0.5即可）

第一类集成算法（拿Boosting来说），有一些注意事项。
Boosting算法要求基学习器能对特定的数据分布进行学习，这可通过重赋权法实施，对无法接受带圈样本的基学习算法，则可通过重采样法来处理，即在每一轮学习中，根据样本分布对训练集重新进行采样，再对基学习器进行训练。需要注意的是，Boosting算法在训练的每一轮都要检查当前学习器是否满足基本条件（上述例子为错误率不超过50%）。

随机森林

在开始随机森林的讨论之前，我们先介绍Bagging算法（属于第二类集成算法）。
Bagging算法的思想比较简单。在样本集合中又放回的抽取T个含m个训练样本的采样集，然后根据每个采样集训练出一个基学习器，再将这些基学习器进行结合。这就是Bagging的流程。
算法步骤如下：
输入：训练集D = {(x1,y1),(x2,y2),…,(xm,ym)};
基学习算法η
训练轮数T
过程：
1:for t = 1,2,…,T Do
2: ht = η(D,B) //B是自助采样产生的样本分布
3:end for
输出：

其中is为指示函数，为真取1，为假取0.

从理论上我们可以知道，好的集成算法里，基学习器应该“好而不同”。如果基学习器效果不好，那么会对集成产生负影响，如果基学习器很类似，那么集成将没有太大意义。

随机森林是Bagging的一个变体。它以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机特征选择。具体来说，传统决策树在选择划分特征时是在当前结点的特征集合中选择一个最优特征；而在随机森林中，对基决策树的每个结点，先从该结点特征集合中随机选择一个包含k个特征的子集，然后从这个子集中选择一个最优特征进行划分。一般情况下，推荐值k = lnd/ln2，其中d为总特征数。

随机森林较好理解，这里不做举例。说一下它的优势：
随机森林中基学习器的多样性不仅来自样本扰动，还来自特征扰动，这就使得最终集成的泛化性能通过个体学习器之间的差异度的增加而进一步提升。
随机森林起始性能往往相对较差（输入特征扰动），然而，随着个体学习器数目的增加，随机森林往往会收敛到更低的泛化误差。值得一提的是，随机森林的训练效率通常优于Bagging。

个人体会

集成学习是一个比较广泛的理论，并不局限于固定的模型。而是偏重于一种思想，并不是说现在固定的一些集成算法（如随机森林），就能把效果做到最好，而是可以在某些集成算法之上，继续集成，以使模型达到更好的效果。
例如我在做某项分类任务时,逻辑回归的精度为79.6%

随机森林精度为81.6%

而用梯度提升树和逻辑回归集成，精度还可以再优化为82.2%

显然是最后一种集成效果最好，而其中的梯度提升树本身就是一种Boosting集成算法，在其中加上Bagging的加权投票思想，与逻辑回归再做一次集成，可以达到比随机森林更好的分类效果。

最后给出Adaboost中分类器权重公式的推导过程，不喜欢数学推导的小伙伴们可以略过。
（这是我发的第二篇博客，还不熟悉用这个打公式，就手写一份）