PhaseDNN: 采用相位技术与神经网络来求解高频波问题
大概从18年开始, 许志钦老师写了一系列有关DeepLearning 与Frequency有关的文章, 里面讲述了深度学习与傅里叶变换之间的关系, 具体可以参见许志钦老师的主页(现在在交大工作) https://ins.sjtu.edu.cn/people/xuzhiqin/
今天,我们介绍一篇与之相关的文章, 题目为:A PHASE SHIFT DEEP NEURAL NETWORK FOR HIGH FREQUENCY APPROXIMATION AND WAVE PROBLEMS. 文章的作者是 Southern Methodist University 的Wei Cai 教授, 下面我们进入正题:
许志钦老师发现了一个现象: 在深度学习中, 将梯度下降方法应用到损失函数时,低频部分的收敛速度要高于高频部分
用定理描述便是
此处我们借用许老师的gif来看这一点(第一张图是原始空间,第二张图是频率空间)(详情见https://ins.sjtu.edu.cn/people/xuzhiqin/fprinciple/ldexperiment.html)
我们的核心想法便是通过相变技术把高频部分转化为低频部分,这样便可以加快网络的收敛速度。
并行方法
具体来说,对于一个给定的频率增量 Δ k \Delta k Δk, 我们说 Δ k = 2 k 0 , \Delta k=2k_0, Δk=2k0, 假定存在某个整数 M>0
s u p p f ^ ( k ) ⊂ [ − M Δ k , M Δ k ] supp \hat{f}(k)\subset [-M\Delta k,M\Delta k] suppf^(k)⊂[−MΔk,MΔk]我们可以构造一个网格区间 [ − M Δ k , M Δ k ] [-M\Delta k,M\Delta k] [−MΔk,MΔk] ,其中 ω j = j Δ k , j = − M , ⋯ , M . \omega _j =j\Delta k, \quad j=-M,\cdots,M. ωj=jΔk,j=−M,⋯,M.我们引入一个单元剖分 { ϕ j k } j = − M M \{\phi_j^k\}_{j=-M}^{M} {ϕjk}j=−MM for the interval [ − M Δ k , M Δ k ] [-M\Delta k,M\Delta k] [−MΔk,MΔk] 1 = ∑ j = − M M ϕ j ( k ) , k ∈ [ − M Δ k , M Δ k ] 1=\sum_{j=-M }^{M}\phi_j(k),\quad k\in [-M\Delta k,M\Delta k] 1=j=−M∑Mϕj(k),k∈[−MΔk,MΔk]
ϕ j ( k ) \phi_j(k) ϕj(k) 最简单的选择便是 ϕ j ( k ) = ϕ ( k − ω j k ) , \phi_j(k)=\phi(\frac{k-\omega_j}{k}), ϕj(k)=ϕ(kk−ωj), 此时 ϕ ( k ) = χ [ − 1 2 , 1 2 ] . \phi(k)=\chi_{[-\frac{1}{2},\frac{1}{2}]}. ϕ(k)=χ[−21,21]. 我们计算 F − 1 ϕ ( k ) \mathcal{F}^{-1}\phi(k) F−1ϕ(k)的Fourier逆变换 , 记作 v, 即 ϕ ∨ ( x ) = 1 2 π s i n ( x / 2 ) x / 2 \phi ^{\vee}(x)=\frac{1}{\sqrt{2\pi}}\frac{sin (x/2)}{x/2} ϕ∨(x)=2π1x/2sin(x/2) ,我们将 f ( x ) f(x) f(x) 在Fourier空间分解 f ^ ( k ) = ∑ j = − M M ϕ j ( k ) f ^ ( k ) = ∑ j = − M M f ^ j ( k ) \hat{f}(k)=\sum_{j=-M}^{M}\phi_j(k)\hat{f}(k) = \sum_{j=-M}^{M}\hat{f}_j(k) f^(k)=j=−M∑Mϕj(k)f^(k)=j=−M∑Mf^j(k)对应着X空间的分解为 f ( x ) = ∑ j = − M M f j ( x ) w h e r e f j ( x ) = F − 1 [ f ^ j ] ( x ) f(x)=\sum_{j=-M}^Mf_j(x)\quad where \;f_j(x)= \mathcal{F}^{-1}[\hat{f}_j](x) f(x)=j=−M∑Mfj(x)wherefj(x)=F−1[f^j](x)可以看出,我们将 f ( x ) f(x) f(x)分为2M+1个函数 f j f_j fj ,其中每个 f j f_j fj的频率均限制在区间 [ ω j − Δ k 2 , ω j + Δ k 2 ] [\omega_j-\frac{\Delta k}{2},\omega_j+\frac{\Delta k}{2}] [ωj−2Δk,ωj+2Δk]之内,因此, 我们可以通过简单的相变来将其频谱变换在 [ − Δ k 2 , Δ k 2 ] [-\frac{\Delta k}{2},\frac{\Delta k}{2}] [−2Δk,2Δk]之内,我们可以通过简单的DNN来快速求解 T j ( x ) T_j(x) Tj(x).
具体来说,以你为 f ^ j ( k ) \hat{f}_j(k) f^j(k) 的支集为 [ ω j − Δ k 2 , ω j + Δ k 2 ] , [\omega_j-\frac{\Delta k}{2},\omega_j+\frac{\Delta k}{2}], [ωj−2Δk,ωj+2Δk], 所以 f ^ j ( k − ω j ) \hat{f}_j(k-\omega_j) f^j(k−ωj) 的支集为 [ − Δ k 2 , Δ k 2 ] , [-\frac{\Delta k}{2},\frac{\Delta k}{2}], [−2Δk,2Δk], 对应的 Fourier 变换
f j s h i f t ( x ) = F − 1 [ f ^ j ( k − ω j ) ] ( x ) f_j^{shift}(x)=\mathcal{F}^{-1}[\hat{f}_j(k-\omega_j)](x) fjshift(x)=F−1[f^j(k−ωj)](x)
可被一个DNN T j ( x ; θ ) T_j(x;\theta) Tj(x;θ) 通过 n 0 n_0 n0 次迭代极小化损失函数 L j ( θ ) = ∫ − ∞ ∞ ∣ f j s h i f t ( x ) − T j ( x ; θ ∣ 2 d x L_j(\theta)=\int_{-\infty}^{\infty}\vert f_j^{shift}(x)-T_j(x;\theta\vert^2dx Lj(θ)=∫−∞∞∣fjshift(x)−Tj(x;θ∣2dx得到。
另外,由 Fourier 的性质有 f j s h i f t ( x i ) = e i ω j x i f j ( x i ) , 1 ≤ i ≤ N , f_j^{shift}(x_i)=e^{i\omega_jx_i}f_j(x_i),1\leq i\leq N, fjshift(xi)=eiωjxifj(xi),1≤i≤N,
一旦我们学习到 f j s h i f t ( x ) f_j^{shift}(x) fjshift(x) , f j ( x ) f_j(x) fj(x) 就可以通过相位变换得到, 即
f j ( x ) ≈ e i ω j x T j ( x , θ ( n 0 ) ) . f_j(x) \approx e^{i\omega_jx}T_j(x,\theta^{(n_0)}). fj(x)≈eiωjxTj(x,θ(n0)).得到所有的 f j ( x ) − M ≤ j ≤ M f_j(x)\; -M\leq j\leq M fj(x)−M≤j≤M 之后,我么那边可以逼近 f ( x ) f(x) f(x) f ( x ) ≈ ∑ j = − M M e − ω j x T j ( x , θ ( n 0 ) ) , f(x)\approx \sum_{j=-M}^M e^{-\omega_jx}T_j(x,\theta ^{(n_0)}), f(x)≈j=−M∑Me−ωjxTj(x,θ(n0)),
其中 θ ( n 0 ) \theta^{(n_0)} θ(n0) 是 n 0 n_0 n0 次训练迭代次数之后的参数值。.
我们的目标是使用如下数据来学习 f ( x ) f(x) f(x)
{ x i , f i = f ( x i ) } i = 1 N . \{x_i,f_i=f(x_i)\}_{i=1}^N. {xi,fi=f(xi)}i=1N.
我们通过如下卷积公式来计算 f j s h i f t ( x ) f_j^{shift}(x) fjshift(x)
f j s h i f t ( x ) = e i ω j x i ϕ j ∨ ∗ f ( x i ) = e i ω j x i ∫ − ∞ ∞ ϕ j ∨ ( x i − x s ) f ( x s ) d s ≈ a δ N s e i ω j x i ∑ x s ∈ ( x i − δ , x i + δ ) ϕ j ∨ ( x i − x s ) f ( x s ) , \begin{aligned} f_j^{shift}(x)&=e^{i\omega_jx_i}\phi_j^{\vee}*f(x_i)=e^{i\omega_jx_i}\int_{-\infty}^{\infty}\phi _j^{\vee}(x_i-x_s)f(x_s)ds\\ &\approx \frac{a\delta}{N_s}e^{i\omega_jx_i}\sum_{x_s\in (x_i-\delta,x_i+\delta)}\phi_j^{\vee}(x_i-x_s)f(x_s), \end{aligned} fjshift(x)=eiωjxiϕj∨∗f(xi)=eiωjxi∫−∞∞ϕj∨(xi−xs)f(xs)ds≈Nsaδeiωjxixs∈(xi−δ,xi+δ)∑ϕj∨(xi−xs)f(xs),
其中 δ \delta δ 满足核函数 ∣ ϕ ∨ ( k ) ∣ \vert \phi^{\vee}(k)\vert ∣ϕ∨(k)∣ 在区间 ( − δ , δ ) . (-\delta ,\delta). (−δ,δ).之外足够得小.
耦合方法
上述方法有很大一部分时间被用来卷积计算(虽然可以并行计算),故我们考虑耦合的方法,即
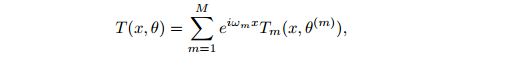
其中 T m T_m Tm 是 DNN 逼近, T(x) 是最后解的逼近.
数值实验
我们采用耦合的方法来复刻文章中的两个数值实验
拟合函数
考虑如下高频函数
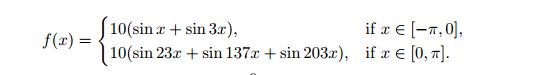
其中, x ∈ [ − π , π ] . x\in [-\pi,\pi]. x∈[−π,π]. 由于它的频谱不是连续的, 故我们只需考虑离散的谱, Δ k = 5 , \Delta k=5, Δk=5,
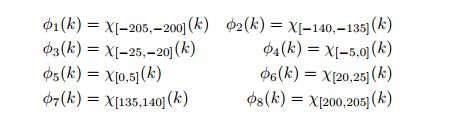
具体细节为
- DNN structure: 1-40-40-40-40-1
- 训练数据 10000个(从 [ − π , π ] [-\pi,\pi] [−π,π] 上从均匀分布采样)
- 测试数据 10000个(从 [ − π , π ] [-\pi,\pi] [−π,π] 上从均匀采点Evenly)
- Adam 初始学习率0.002
- 迭代次数 1000
- Batchsize 2000
训练结果为
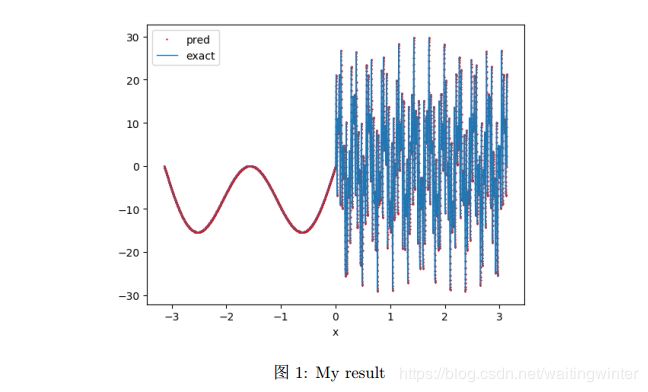
局部结果为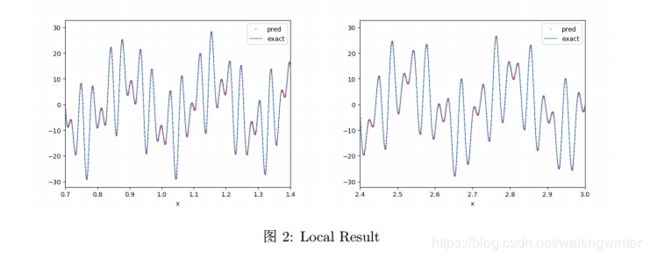
L 2 L^2 L2相对误差为
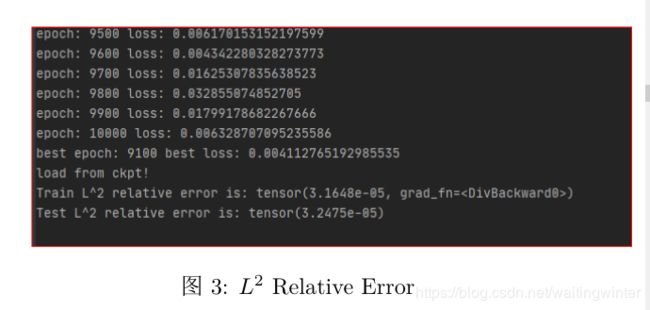
求解方程
考虑如下方程
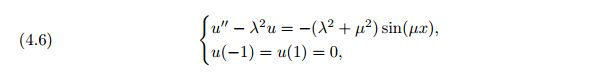
精确解为
![]()
λ = 3 , μ = 250 , o m e g a m = { 0 , μ } , \lambda=3,\mu=250,omega_m=\{0,\mu\}, λ=3,μ=250,omegam={0,μ},数值结果如下
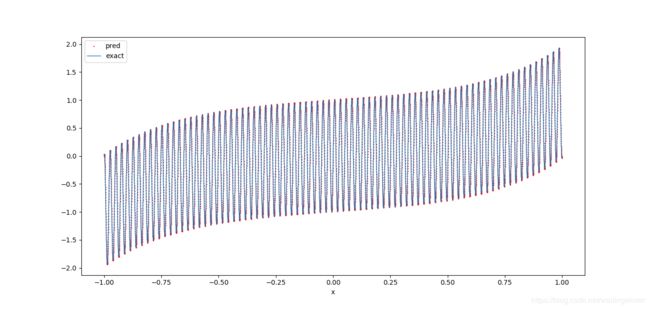
局部结果为
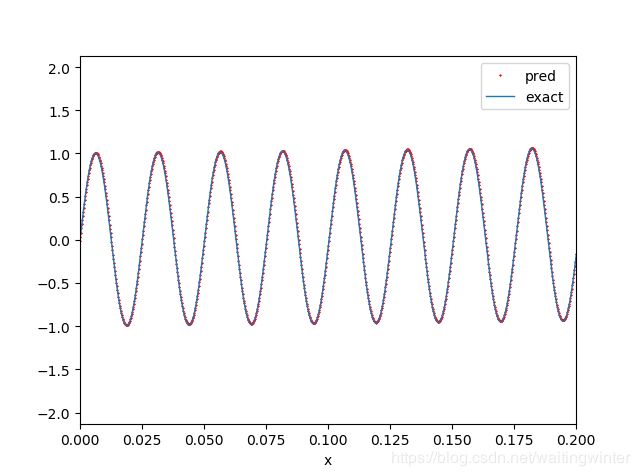
训练误差为