人工神经网络：感知器

人工神经网络：感知器

• 1.1 基本概念

1、输入节点：X1={x1,x2,x3,...,xi,...xn},for example，X1=[1 2]';

2、输出节点：y={y1,y2},for example,y=[0 1];

3、权值：W={w1,w2,w3,...,wi,...,wn},for example,W=[1 1];感知器学习规则只适用于二进制神经元，初始权值可取任意值。
感知器学习规则代表一种有监督学习。由于感知器理论是研究其它神经网络的基础，该规则对于神经网络的有监督学习具有极为重要的意义。

4、偏置因子：b,for example b=1，注意：外部偏置值恒为1;（但标准不同时，该值也可能不同）

5、激活函数：f，激活函数的意义是y=f(w1*x1+w2*x2+w3*x3+,...,+wn*xn+b);

hardlim函数：a=hardlim(n),当n>=0时，a=1,否则a=0;hardlims函数：a=hardlims(n),当n>=0,a=1,否则，a=-1。

6、学习算法：神经网路对权值的调整过程。

7、结构模型：无。

在二维空间中，单层感知器进行模式识别的判决超平面由下式决定：

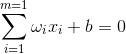
• 1.2 案例分析1

1、输入节点 X=[2 1]' ，输出节点 y=1，期望输出 t=0，权值 W=[0 0]'，W(t+1)=W(t)+eX，

2、计算过程：

以下t为target的简称，e为error的简称，

（1）首先输入两个节点X=[2 1]'，目标输出target=0，权值初始化为W=[0 0]'， 先不考虑偏置因子值b（b的输入永远为1），即将b设为0，则输出为y=f(w1*x2+w2*x1)=f(2*0+1*0)=1。

（2）输出结果y=1与目标值target=0不一致，误差error=target-y=-1，因此根据反馈结果调整权值W，权值W的调整公式W(t+1)=W(t)+eX进行调整，调整后W(1)=[0 0]'+(-1)[2 1]'=[-2 -1]'。此次权值将b也加进去，不对偏置因子b单独使用公式进行计算，如此使得W(1)=[-2 -1 -1]'，W(1)=[0 0 0]'+(-1)[2 1 1]'=[-2 -1 -1]'。

（3）再次输入，y=f(w1*x2+w2*x1+b)=f(2*(-2)）+1*(-1)+1*(-1))=0，输出结果与期望值t一致，建立网络。

• 1.3 案例分析2

样本X=[2 1 -2 -1;2 -2 2 0]，即样本X(1)=[2 2]'，X(2)=[1 -2]'，X(3)=[-2 2]'，X(4)=[-1 0]'，期望分别为t(1)=0，t(2)=1，t(3)=0，t(4)=1，初始化权值、阈值w(1)=0，w(2)=0，b=0。

（1）将样本X(1)输入，则y(1)=hardlim(w(1)*2+w(2)*2+b)=hardlim(0)=1。

（2）计算输出值与目标值的误差e=t(1)-y(1)=0-1=-1。

（3）根据误差调整权值和阈值W=W+eX(1)'=[0 0 0]'+(-1)[2 2 1]'=[-2 -2 -1]'。

（4）输入样本X(2)，则y(2)=hardlim(w(1)*1+w(2)*(-2)+b)=hardlim(-2+4-1)=1。

（5）计算输出值与目标值的误差e=t(2)-y(2)=1-1=0。

（6）因为误差为e=0，所以权值和阈值不再发生变化。

（7）输入样本X(3)，则y3=hardlim(w(1)*(-2)+w(2)*2+b)=hardlim(4-4-1)=0。

（8）计算输出值与目标值的误差e=t(3)-y(3)=0-0=0。

（9）输入样本X(4)，则y(4)=hardlim(w(1)*(-1)+w(2)*0+b)=hardlim(1)=1。

（10）计算输出值与目标值的误差e=t(4)-y(4)=1-1=0。

（11）从第一个样本开始，再来一遍，验证权值和阈值。

 

 

 

 

 

 

 

 

 

 

 

 

 

参考文献：

本文主要参考以下文献

Matlab2016数值计算与智能算法，www.51zxw.net