ZOJ 1805 Squadtrees(四分树难题)
Squadtrees
题目传送门~
Time Limit: 5000 msMemory Limit: 32768 KB
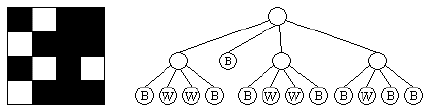
Quadtrees are data structures used to store digital images. For our purposes, the images will be simple bitmaps, where every pixel is either a 1 (black) or a 0 (white). A quadtree representation of a bitmap is obtained as follows: first, associate the root node with the entire image. If the entire image is either all 1's or all 0's, then store that value in the node and you're done. Otherwise divide the region into four equal size quadrants, add four children to the root, and assign each child one of the four regions in the following order: the first child gets the upper left quadrant, the second the upper right, the third the lower left and the fourth the lower right. Then recursively apply the above rules to each of the children. For example, the 4x4 image on the left would be represented by the quadtree on the right:
Note that this procedure only works as stated if the image is a square and has a side length equal to a power of 2. For those images which do not meet those requirements, we pad the rows and columns with 0's (on the right and on the bottom, respectively) until we have a bitmap of the appropriate size. For example, a 5x13 image would be converted to a 16x16 bitmap (with the original image residing in the upper left portion, and the remainder of the image filled with 0's).
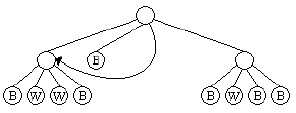
While quadtrees can result in a significant savings in space over the original image, even more savings can be achieved if we identify repeated subtrees. For example, in the tree above, the first and third subtrees of the root are identical, so we could replace the root of the third subtree with a reference to the first subtree, obtaining something that symbolically looks like the following:
We will call these compressed quadtrees super quadtrees, or squadtrees. For our purposes the use of a reference saves space only when the tree it replaces has height of at least 1. Thus, while we could replace 5 of the nodes which contain a B with references to the first node with a B, this would not in practice save any space in the compression. Using this rule, our squadtree contains only 12 nodes, as opposed to 17 in the original quadtree. Your job for this problem is to take a set of images and determine the number of nodes in both the resulting quadtrees and squadtrees.
Input
Input will consist of multiple problem instances. Each instance will start with a single line containing two integers n and m, indicating the number of rows and columns in the image. The maximum values for these integers is 128. The next n lines will each contain m characters representing the image to process. A black pixel will be represented by a '1', and a white pixel will be represented by a '0'. The input line 0 0 will terminate input and should not be processed.
Output
For each problem instance, output two integers separated by a single space. The first value is the number of nodes in the quadtree for the problem instance, and the second is the number of nodes in the squadtree.
Sample Input
4 4
1011
0111
1010
0111
6 7
1110111
1010101
0000000
0100010
1011101
1010101
0 0
Sample Output
17 12
61 24
题后两句话:
①啊啊啊啊这个题...有点难还有点妙~并没有像1788里需要你扫描整个四分树把编码整出来,而是统计quadtrees和super quadtrees的节点数即可
②所以这题就一边搜索建立四分树一边统计节点数就好,然后需要压缩的地方特别处理,不需要把两棵树都生成出来再统计。
③总的来说这题不简单,但是理清思路再借鉴大佬的想法就可以把这个题整出来了,加油加油啊~四分树就告一段落啦!!!
嘻嘻嘻嘻,上才艺啦~
#include
#include
#include
using namespace std;
struct quadtree{
int q1,q2,q3,q4;
quadtree(){}
quadtree(int num1,int num2,int num3,int num4){
q1=num1,q2=num2,q3=num3,q4=num4;
}
bool isequal(int num1,int num2,int num3,int num4){ //检查该节点存放的四个孩子是否相同
return q1==num1&&q2==num2&&q3==num3&&q4==num4;
}
}tree[16666];
int n,m,point,qt1,qt2; //n行m列; point为节点编号; qt1为quadtrees的数量,qt2为super quadtrees(压缩) 的数量
char str[150][150]; //输入字符矩阵
int map[150][150]; //存放数字矩阵
//组织输入并初始化
void init(){
memset(map,0,sizeof(map));
for(int i=0;i>1,collength=y+col>>1; //map四分(>>1相当于/2)
//四个方向分别递归调用DFS,找到其子嗣的节点值
int child1=DFS(x,y,rowlength,collength);
int child2=DFS(x,collength+1,rowlength,col);
int child3=DFS(rowlength+1,y,row,collength);
int child4=DFS(rowlength+1,collength+1,row,col);
if(child1==0&&child2==0&&child3==0&&child4==0) { qt1-=4,qt2-=4;return 0;} //如果该节点四个孩子的节点值全为0,则合并其子嗣并将节点值置为0
if(child1==1&&child2==1&&child3==1&&child4==1) { qt1-=4,qt2-=4;return 1;} //如果该节点四个孩子的节点值全为1,则合并其子嗣并将节点值置为1
for(int i=2;i