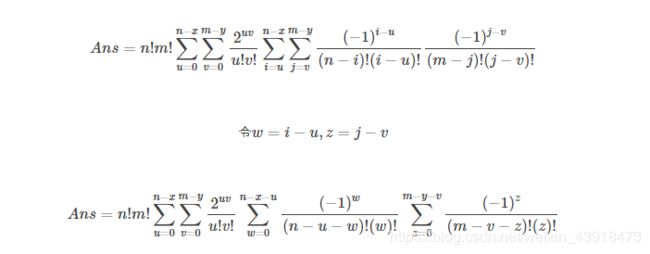2018HDU多校训练2

题目链接：https://cn.vjudge.net/contest/299050

A - Absolute

HDU - 6309

代码来源：https://cn.vjudge.net/status/#un=&OJId=HDU&probNum=6309&res=1&language=&onlyFollowee=false
题目大意：给定n个区间$[li,ri]$，${-10}^6\le li\le ri\le 10^6$且$li,ri$都为整数，xi为对应范围内的一个随机实数，求|∑xi|的期望。n≤15，答案对998244353取模。

#include
#include
using namespace std;
#define ll long long
const int mod=998244353;

int l[15],r[15],n;
ll quickpower(ll x,ll y)
{
	ll res=1;
	while(y){
		if(y&1) res=res*x%mod;
		y>>=1;
		x=x*x%mod; 
	}
	return res;
}
ll sgn(ll x)
{
	return x>0?1:-1;
}
ll dfs(int deep,ll x=0){
	if(deep==n){
		return quickpower(x,n+1)*sgn(x);
	}
	return ((dfs(deep+1,x+r[deep])-dfs(deep+1,x+l[deep]))%mod+mod)%mod;
}
int main()
{
	scanf("%d",&n);
	ll ans=1;
	for(int i=0;i<n;i++){
		scanf("%d%d",&l[i],&r[i]);
		ans=ans*(r[i]-l[i])*(i+2)%mod;
	}
	ans=quickpower(ans,mod-2)*dfs(0)%mod;
	printf("%lld\n",(ans+mod)%mod);
	return 0;
} 

B - Counting Permutations

HDU - 6310

题解转载自：https://www.cnblogs.com/163467wyj/p/9369034.html

#include 
using namespace std;
#define rep(i,a,n) for (int i=a;i
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
// head
 
const int N=220;
int dp[N][1010],comb[N][N],fr[N],n,x;
ll tmp[1010];
ll mod=1000000007,mod2;
int main() {
    scanf("%lld",&mod);
    mod2=mod*mod;
    rep(i,0,201) {
        comb[i][0]=comb[i][i]=1;
        rep(j,1,i) comb[i][j]=(comb[i-1][j-1]+comb[i-1][j])%mod;
    }
    dp[0][0]=1; fr[0]=0;
    dp[1][1]=1; fr[1]=1;
    for (int i=2;i<=200;i++) {
        for (int j=0;j<i;j++) {
            int l=j,r=i-1-j,x=min(l,r)+1;
            if (l>r) break;
            fr[i]=max(fr[i],x+fr[l]+fr[r]);
            rep(k,0,fr[l]+fr[r]+1) tmp[k]=0;
            for (int pl=l;pl<=fr[l];pl++) {
                for (int pr=r;pr<=fr[r];pr++) {
                    tmp[pl+pr]=tmp[pl+pr]+(ll)dp[l][pl]*dp[r][pr];
                    if (tmp[pl+pr]>=mod2) tmp[pl+pr]-=mod2;
                }
            }
            ll coef=comb[i-1][l]; if (l<r) coef=coef*2%mod;
            rep(k,0,fr[l]+fr[r]+1) {
                dp[i][k+x]=(dp[i][k+x]+tmp[k]%mod*coef)%mod;
            }
        }
    }
    while (scanf("%d%d",&n,&x)!=EOF) {
        if (x>fr[n]) puts("0");
        else printf("%d\n",dp[n][x]);
    }
}

C - Cover（输出欧拉路径）

HDU - 6311

题解转载自：https://www.cnblogs.com/xiuwenli/p/9372062.html
弗莱德算法实现：https://blog.csdn.net/zitian246/article/details/76096140
弗莱德算法介绍：https://www.cnblogs.com/new-zjw/p/8541027.html
题意：有最少用多少条边不重复的路径可以覆盖一个张无向图。
分析：对于一个连通块（单个点除外），如果奇度数点个数为 k，那么至少需要max{k/2,1} 条路径。将奇度数的点两两相连边（虚边），然后先从奇度数的点出发，搜索由其出发的欧拉回路。需要将遍历的边和其反向边打标记，并在DFS退栈的时候记录边的编号（前向星的存储是访问后加入的边），若该边是自己添加的虚边，那么说明实际上这次DFS搜索到的是一条欧拉通路，那么结果还需额外+1，所以对所有奇数点DFS过后，得到的结果就是max{k/2,1}。
再从未被访问过的偶数顶点出发搜索由其出发的欧拉回路，每一次DFS就是找到了一条回路。

#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn =1e5+5;
struct Edge{
    int to,id,next;
    bool f;
}edges[maxn<<4];
int tot,head[maxn],cnt;
bool vis[maxn];
vector<int> res[maxn];
int deg[maxn];

void init()
{
    tot=0;
    cnt=0;
    memset(deg,0,sizeof(deg));
    memset(vis,0,sizeof(vis));
    memset(head,-1,sizeof(head));
}

void AddEdge(int u,int v ,int id)
{
    edges[tot].f = 0;edges[tot].to=v;edges[tot].id = id;edges[tot].next =head[u];
    head[u]=tot++;
}

void dfs(int u)
{
    vis[u]=true;
    //cout<
    for(int i=head[u];~i;i=edges[i].next){
        int v =edges[i].to,id =edges[i].id;
        if(!edges[i].f){
            edges[i].f = edges[i^1].f = true;       //
            dfs(v);
            if(id) res[cnt].push_back(-id);     //
            else cnt++;                         //扫到虚边 路径+1 
            //cout<
        }
    }
}

void Print()
{
    printf("%d\n",cnt);
        for(int i=1;i<=cnt;++i){
            printf("%d",res[i].size());
            int k = res[i].size();
            for(int j=0;j<k;++j) printf(" %d",res[i][j]);
            printf("\n");
            res[i].clear();  
    }
}

int main()
{
    #ifndef ONLINE_JUDGE
        freopen("in.txt","r",stdin);
        freopen("out.txt","w",stdout);
    #endif
    int T,N,M,u,v,tmp;
    while(scanf("%d%d",&N,&M)==2){
        init();
        for(int i=1;i<=M;++i){
            scanf("%d%d",&u,&v);
            deg[u]++,deg[v]++;
            AddEdge(u,v,i);
            AddEdge(v,u,-i);
        }
        u=0;
        for(int i=1;i<=N;++i){
            if(deg[i]&1){
                if(u){ 
                    AddEdge(u,i,0);
                    AddEdge(i,u,0);
                    u=0;  
                }          //将奇数点两两连边 
                else u=i;
            }
        }
        for(int i=1;i<=N;++i){
            if(!vis[i] && (deg[i]&1)){   
                cnt++;  
                dfs(i);
                cnt--;
            }
        }
        for(int i=1;i<=N;++i){
            if(!vis[i] && deg[i]){
                cnt++;
                dfs(i);
            }
        }
        Print();
    }
    return 0;
}

D - Game

HDU - 6312

题解参考：https://blog.csdn.net/BePosit/article/details/83996119
题意：1-n个数，Alice Bob 轮流取，必须去一个数连同它所有的因数一起取走。
思路：SG无法大表，但一定不会有平局，所有终归会有一个必胜态，我们可以先不看1。
则2-n一定有一个胜者，如果这个状态A胜的话，我们就可以选择那个让我们胜的数。
因为1是所有数的因子所以1也会被删去，如果A输，我们可以先去掉1来转变状态。这样A还是会胜。

#include
#include
#include
#include
#include
using namespace std;
const int maxn=300010;

int n,a[maxn];

int main()
{
	while(~scanf("%d",&n)){
		printf("Yes\n");
	}
	return 0;
}

E - Hack It

HDU - 6313
题意：输出一个维度不超过2000的01矩阵，要求这个矩阵的所有子矩阵都不存在四个角都是1的情况。且这个矩阵含1的个数不小于85000。
题解：$\sqrt{2000}$是44点多，对于85000，发现取$2000\ast \sqrt{2000}$恰好超过85000，我们可以构造一个含$\sqrt{n}\ast \sqrt{n}$个小矩阵的矩阵，每个矩阵含1的个数是$\sqrt{n}$个，则总的含1个数是$\sqrt{n}\ast \sqrt{n}\ast \sqrt{n}$，$n$取45、46是合数，不好构造，取47恰好，至于如何构造子矩阵使其含1个数是$\sqrt{n}$。可以看代码，自行画图脑补下。

#include 
using namespace std;
int mod=47;
int mmap[3000][3000];
int main()
{
    for(int i=0; i<mod; i++)//第i大行 
        for(int j=0; j<mod; j++)//第j小行/列 
            for(int k=0; k<mod; k++)//第k大列 
            {
                int x=i*mod;
                int y=k*mod;
                int X=x+j;
                int Y=y+(j*k+i)%mod;
                mmap[X][Y]=1;
            }
    printf("2000\n");
    for(int i=0; i<2000; i++)
    {
        for(int j=0; j<2000; j++)
            printf("%d",mmap[i][j]);
        printf("\n");
    }
    return 0;
}

F - Matrix

HDU - 6314
题解转载自：https://blog.csdn.net/qq_32506797/article/details/81227571
题意：$n\ast m$的方格，黑白染色，至少x行，y列全是黑色的方案数。
题解：令$f(n,m)$为$n\ast m$的方格，没有任意一行，任意一列全是黑色的方案数。公式推导过程如下，预处理各个部分。

#include
using namespace std;
#define ll long long

const int N = 3e3+5;
const int MOD = 998244353;


int pre[N][N], gg[N][N], inv[N], fac[N], p[N*N];

void init() {
    inv[1] = 1;
    for(int i = 2; i < N; ++i)//逆元 
        inv[i] = MOD-(1LL*MOD/i*inv[MOD%i]%MOD);
    
    fac[0] = 1, inv[0] = 1;//阶乘 阶乘逆元 
    for(int i = 1; i < N; i++){
        fac[i] = (1LL*fac[i-1]*i)%MOD;
        inv[i] = 1LL*inv[i-1]*inv[i]%MOD;
    }
    p[0] = 1;//2^i 
    for(int i = 1; i < N*N; i++) {
        p[i] = p[i-1]+p[i-1];
        if(p[i] >= MOD) p[i] -= MOD;
    }
    for(int u = 0; u < N; u++) {
        for(int v = 0; v < N; v++) {
            gg[u][v] = 1LL*p[u*v]*inv[u]%MOD*inv[v]%MOD;
        }
    }
    for(int u = 0; u < N; u++) {
        for(int v = 0; v <= u; v++) {
            int t = 1LL*inv[u-v]*inv[v]%MOD;
            if(v & 1) t = MOD-t;
            pre[u][v] = (v?pre[u][v-1]:0)+t;
            if(pre[u][v] >= MOD) pre[u][v] -= MOD;
        }
    }
}

int main() {
    init();
    int n, m, x, y;
    while(~scanf("%d%d%d%d", &n, &m, &x, &y)) {
        ll ans = 0;
        for(int u = 0; u <= n-x; u++) {
            for(int v = 0; v <= m-y; v++) {
                ans += 1LL*gg[u][v]*pre[n-u][n-x-u]%MOD*pre[m-v][m-y-v]%MOD;
                if(ans >= MOD) ans -= MOD;
            }
        }
        ans = ans*fac[n]%MOD*fac[m]%MOD;
        printf("%lld\n", ans);
    }
    return 0;
}

G - Naive Operations

HDU - 6315
题解参考：https://blog.csdn.net/iwts_24/article/details/81841968
题意：给一个长度n值为0的区间数组a，和长度为n的一个排列b，有q次操作，add（l,r）表示a的l，r区间内的数+1。query(l,r)表示查询一个区间内ai/bi的值。
题解：对于序列b，我们可以在每次add的时候，减一，当减到0说明可以发生整除了，此时sum线段树的对应结点+1。线段树$mn[]$储存区间最小值
修改区间时的核心处理：

if(mn[k]>1&&l>=a&&r<=b){//如果该区间被包含，我们直接更新父节点的mn值，设置下懒惰标志
    mn[k]--;
    lazy[k]++;//
    return;
}
if(l==r&&mn[k]==1){//如果该区间是叶子结点，直接更新sum值
    sum[k]++;
    lazy[k]=0;//
    mn[k]=c[l];
    return;
}

代码如下

#include
#include
#include
#include
#include
using namespace std;
#define ll long long
const int maxn=100010;

ll sum[maxn<<2];
int mn[maxn<<2];
int lazy[maxn<<2];
int c[maxn],n,q;
ll ans;
void pushup(int k)
{
    sum[k]=sum[k*2]+sum[k*2+1];
    mn[k]=min(mn[k*2],mn[k*2+1]);
    
}
void build(int k,int l,int r)
{
	lazy[k]=0;//--------------------------毒瘤 开始初始化没放外面，wa哭。。
    if(l==r){
        sum[k]=0;
        mn[k]=c[l];
        return;
    }
    int m=(l+r)/2;
    build(k*2,l,m);
    build(k*2+1,m+1,r);
    pushup(k);
}
void pushdown(int k)
{
    lazy[k*2]+=lazy[k];
    lazy[k*2+1]+=lazy[k];
    mn[k*2]-=lazy[k];
    mn[k*2+1]-=lazy[k];
    lazy[k]=0;
}
void update_interval(int k,int l,int r,int a,int b)
{
    if(mn[k]>1&&l>=a&&r<=b){
        mn[k]--;
        lazy[k]++;//
        return;
    }
    if(l==r&&mn[k]==1){
        sum[k]++;
        lazy[k]=0;//
        mn[k]=c[l];
        return;
    }
    if(lazy[k])
        pushdown(k);
    int m=(l+r)/2;
    if(a<=m) update_interval(k*2,l,m,a,b);
    if(m<b) update_interval(k*2+1,m+1,r,a,b);
    pushup(k);
}
void query_interval(int k,int l,int r,int a,int b)
{
    if(l>=a&&r<=b){
        ans+=sum[k];
        return;
    }
    if(lazy[k])
        pushdown(k);
    int m=(l+r)/2;
    if(a<=m) query_interval(k*2,l,m,a,b);
    if(m<b) query_interval(k*2+1,m+1,r,a,b);    
    pushup(k);
}
int main()
{
    while(~scanf("%d%d",&n,&q)){
        for(int i=1;i<=n;i++){
            scanf("%d",&c[i]);
        }
        build(1,1,n);
        int a,b;
        char op[10];
        while(q--){
            scanf("%s%d%d",op,&a,&b);
            if(op[0]=='a'){
                update_interval(1,1,n,a,b);
            }else{
                ans=0;
                query_interval(1,1,n,a,b);
                printf("%lld\n",ans);
            }
        }
    }
    return 0;
}

H - Odd Shops（看不懂系列）

HDU - 6316
题解转载自：https://www.cnblogs.com/Cool-Angel/p/9380809.html

这道题目，首先答案显然为$(1+{\sum }_{i=1}^{10}ai\ast xi{)}^n$中系数为奇数的项有几个

那么我们只要对该式进行处理就行了 首先我们设关注到题目要求统计的是系数为奇数，那么相当于在mod 2意义下进行运算
我们现在来考虑一个子问题，${f(n)}^{2k}\ast g(n)$中有几个系数为奇数
对于该式，我们意识到前一个式子是${({f(2n)}^k)}^2$因为是平方，所以打开之后两项相乘的系数就会消掉 例如$(a+b{)}^2=a^2+b^2+2ab$最后一项对答案显然没有贡献，也就是说平方后我们关心的只是一个与原串相同的串
对于g(n)，我们将其拆分成g(n)=o(n)+e(n)，o(n)为g(n)中奇数次方的项，e(n)为g(n)中偶数次方的项，由于${({f(2n)}^k)}^2$只剩下平方项，所以o(n)与e(n)对答案的贡献是独立的
那么最后一步就是递归拆分后递归求解这个问题，顺便加个map瞎记忆化一下就过了
为什么我们要进行这个拆分呢？ 我们可以很快发现这样拆分之后递归求解的时候o(n)和e(n)的项数就可以从20降为10，这样就可以将一个$10^{10}$项的多项式希望得到的结果，只用10位的二进制数得到答案 题解是这么想，代码也确实是这么打，但是这个代码还是比较巧妙的

#include
#include
#include
#define ll long long 
using namespace std;
map<pair<ll,ll>,ll> mp;
ll mo=998244353,x;
ll mul(ll a,ll b){
    ll ret=0;
    while (b){
        ret^=a*(b&(-b)),b-=b&(-b);
    }
    return ret;
}
ll f(ll n,ll g){
    if (mp.count(make_pair(n,g)))return mp[make_pair(n,g)];
    ll &ret=mp[make_pair(n,g)];
    if (!n)return ret=__builtin_popcountll(g)%mo;
    if ((n&1))g=mul(g,x);ll a=0,b=0;
    for (int i=0;i<=25;i++)if ((g&(1<<i))){
        if ((i&1))a|=(1<<(i>>1));
        else b|=(1<<(i>>1));
    }
    return ret=(f(n>>1,a)+f(n>>1,b))%mo;
}
int a[15],n;
int main(){
    while (~scanf("%d",&n)){
        mp.clear();
        x=1;
        for (int i=1;i<=10;i++){
            scanf("%d",&a[i]);
            if ((a[i]&1))x|=(1<<i);
        }
        ll ans=f(n,1);
        printf("%d\n",ans);
    }
}

J - Swaps and Inversions

HDU - 6318
题意：给一组数，数出总的逆序对，逆序对乘以x是你要付出的代价，你也可以选择交换相邻的数，但要付出y的代价，由于交换相邻的数，逆序对减1，我们可以理解成，最终答案即是逆序对*min(x,y)
求逆序对方法
1.利用归并排序

#include
#include
#include
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
const int maxn=100010;

int n,a[maxn],x,y;
int L[maxn],R[maxn];

ll merge(int l,int m,int r)
{
	int n1=m-l;
	int n2=r-m;
	for(int i=0;i<n1;i++) L[i]=a[l+i];
	for(int i=0;i<n2;i++) R[i]=a[m+i];
	L[n1]=R[n2]=inf;
	int i=0,j=0;
	ll res=0;
	for(int k=l;k<r;k++){
		if(L[i]<=R[j]){
			a[k]=L[i++];
		}else{
			a[k]=R[j++];
			if(i<n1) res+=1LL*(n1-i);//
		}
	}
	return res;
}
ll mergeSort(int l,int r)
{
	if(l+1>=r) return 0;
	int m=(l+r)/2;
	ll res=0;
	res+=mergeSort(l,m);
	res+=mergeSort(m,r);
	res+=merge(l,m,r);
	return res;
}
void print()
{
	for(int i=0;i<n;i++)
		printf("%d ",a[i]);
	printf("\n");
 } 
int main()
{
	while(~scanf("%d%d%d",&n,&x,&y)){
		for(int i=0;i<n;i++){
			scanf("%d",&a[i]);
		}
		ll res=mergeSort(0,n);
		printf("%lld\n",res*min(x,y));
	}
	return 0;
}

2.用树状数组，需要离散化处理。

#include 
using namespace std;
typedef long long ll;
const int mmax = 1e5 + 5;
int ans[mmax],ans1[mmax];
struct Node
{
    int value,i;
    bool operator <(const Node &b)const
    {
        return value<b.value;
    }
} a[mmax];
int lowbit(int k)
{
    return k&(-k);
}
int sum(int p)
{
    int res = 0;
    while(p)
        res += ans[p],p -= lowbit(p);
    return res;
}
void add(int x,int d)
{
    while (x<=mmax)
    {
        ans[x]+=d;
        x += lowbit(x);
    }
}

int main()
{
    ll  n, x,y, left, right;
    ll mans;
    while (scanf("%lld%lld%lld", &n,&x,&y)!=EOF)
    {
        mans = 0;
        memset(ans, 0, sizeof(ans));
        memset(ans1, 0, sizeof(ans1));
        /** 散列 **/
        for (int i = 1; i <= n; i++)
        {
            scanf("%d",&a[i].value);
            a[i].i = i;
        }
        sort(a + 1, a + n + 1);
        int index = 1;
        ans1[a[1].i] = 1;
        for (int i = 2; i <= n; i++)
        {
            if (a[i].value == a[i - 1].value)
                ans1[a[i].i] = index;
            else
                ans1[a[i].i] = ++index;
        }
        /**/
        for (int i = 1; i <= n; i++)
        {
            mans+=sum(ans1[i]);
            add(ans1[i],1);

        } mans=n*(n-1)/2-mans;
        cout<<(mans*min(x,y))<<endl;
    }
    return 0;
}