MATLAB学习系列——线性代数实验
矩阵
矩阵创建
syms x;
F=sym([cos(x),sin(x);2*x,log10(x)])
F =
[ cos(x), sin(x)]
[ 2*x, log(x)]
zeros(n,m) % n行m列零矩阵
ones(n,m) % n行m列壹矩阵
rand(n,m) % n行m列随机阵
randn(n,m) % n行m列正态随机阵
eye(n) % n阶单位阵
magic(n) % n阶幻方阵幻方阵的每行元素之和、每列元素之和、对角线元素之和皆相同。
vander(c) % 由向量c构成的范德蒙矩阵
矩阵操作
a=rand(10);
[i,j]=find(a==0.31);%找数组中数值为0.31的坐标
a1=a([1,3,],:);%提取数组中第一行第三行数据(列操作同理)
a2=a([2,3],[2,3]) %提取子矩阵
a3=a(3)
a4=a(:) %按照列优先顺序输出
a(:,3)=[]; %将第三列删除
b=[1 2 3 4 5 6 7 8 9 10];
a(:,1)=b';%将第一列替换成b的转置
数据操作
std(A) 求矩阵A列元素的标准差
mean(A) 求矩阵A列元素的均值
sum(A) 求矩阵A各列元素的和
prod(A) 求矩阵A各列元素的积
cumsum(a) 求列元素的累计和
cumprod(a) 求列元素的累计积
cumtrapz(a) 梯形法求累积数值积分
sort(a) 按升序对每列元素进行排序
sortrows(a) 按升序排列矩阵各行(按首列)
%最值
min(a) %每一列最小值
min(a(:)) %所有最小值
max(a)
[t1,t2]=bounds(a) %同时求得最大最小值
t=median(a) %中位数
t=mode(a) %众数
方差
a=[1 6 6;4 2 5; 7 2 3];
x1=var(a); %默认为0,等价于x1=var(a,0) ,除以N-1,结果 9.0000 5.3333 2.3333
x2=var(a,1); %此时除以N,结果6.0000 3.5556 1.5556
x3=var(a,0,1); %除以N-1, 9.0000 5.3333 2.3333
x4=var(a,0,2); %除以N-1,[8.3333;2.3333;7.0000]列向量
x5=var(a,1,1); %除以N,求出每列的方差,6.0000 3.5556 1.5556
x6=var(a,1,2);%除以N,求出每行的方差,[5.5556;1.5556;4.6667]
%协方差
x7=cov(a);
%相关系数可以先计算协方差,然后除以各自标准差的乘积
%如果给定两个向量可以用t=corrcoef(a,b)求定相关系数
矩阵运算
A' A的转置
det(A) A的行列式
rank(A) 矩阵的秩
inv(A) 矩阵求逆
compan(A) A的伴随矩阵
[D,X]=eig(A) A的特征值与特征向量
[D为特征向量构成的方阵;X是特征值构成的对角阵]
norm(A) 矩阵的范数
orth(A) 矩阵的正交化
poly(A) 特征多顶式
rref(A) 阶梯状行的 最简式
size(A) 测矩阵长度(行,列)
A\b 等价于 ( A ) − 1 ∗ b (A)^{-1}*b (A)−1∗b
多项式
构造多项式
用系数构造
默认为x
c=[2 6 0 -3 2 4];
f = poly2sym(c)
如果打印未知数是y
syms y;
c=[2 6 0 -3 2 4];
f = poly2sym(c,y)
结果:f =
2x^5 + 6x^4 - 3x^2 + 2x + 4
用根构造
r=[6 0 -3 2];
c=poly(r); %用poly函数通过根求解多项式系数
f=poly2sym(c)
多项式求根
例如:求解 x 3 − 7 x − 6 = 0 x^3-7x-6=0 x3−7x−6=0的根。
c=[1 0 -7 6]; %多项式的系数向量
r=roots(c); %求根
多项式和差乘积
例如: a ( x ) = x 3 + 2 x 2 + 3 x 和 b ( x ) = x 3 + 4 x 2 + 9 x + 16 的 求 和 差 乘 积 a(x)=x^3+2x^2+3x和b(x)=x^3+4x^2+9x+16的求和差乘积 a(x)=x3+2x2+3x和b(x)=x3+4x2+9x+16的求和差乘积
a=[1 2 3 4];
b=[1 4 9 16];
c1=a+b;
c2=a-b;
c3=conv(a,b);%卷积运算
f=poly2sym(c1)
f=poly2sym(c2)
f=poly2sym(c3)
多项式除法
例如:c3除以a:
[q,r]=deconv(c3,a)
%q是商多项式的系数向量,r 是余数多项式的系数向量。
多项式微分
a=[1 3 4 -6 4 -7 12];
a1=polyder(a)%求微分
ff=poly2sym(a1)
多项式估值
x=1:6;
v=polyval(a,x)
多项式拟合
polyfit(x,y,n)
%表示用最小二乘法对数据x,y进行n阶多项式函数拟合
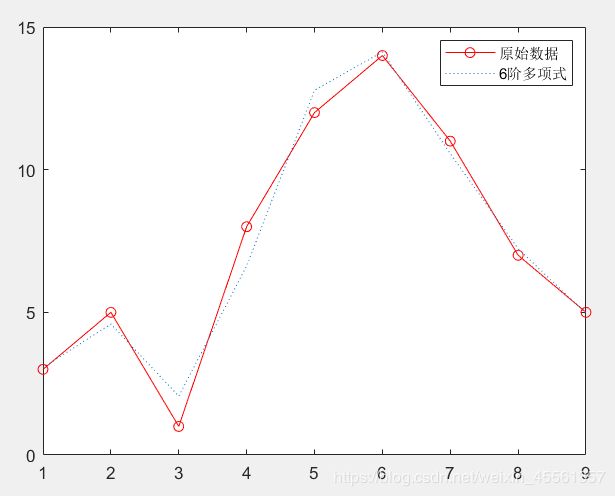
x=1:9;
y=[3 5 1 8 12 14 11 7 5];
c=polyfit(x,y,6); 6次多项式拟合
z=polyval(c,x);
plot(x,y,'ro-',x,z,':')
legend('原始数据','6阶多项式')