复杂性思维中文第二版 六、生命游戏
六、生命游戏
原文:Chapter 6 Game of Life
译者:飞龙
协议:CC BY-NC-SA 4.0
自豪地采用谷歌翻译
在本章中,我们考虑二维细胞自动机,特别是 John Conway 的生命游戏(GoL)。 像上一章中的一些 CA 一样,GoL 遵循简单的规则并产生令人惊讶的复杂行为。 就像沃尔夫勒姆的规则 110 一样,事实证明 GoL 是通用的;也就是说,至少在理论上它可以计算任何可计算的函数。
GoL 的复杂行为引发了科学哲学问题,特别是科学现实主义和工具主义的相关问题。 我讨论这些问题并提出扩展阅读的建议。
在本章的最后,我演示了如何在 Python 中高效实现 GoL。
本章的代码位于本书仓库的chap06.ipynb中。 使用代码的更多信息,请参见第?节。
6.1 Conway 的生命游戏
首先要研究的细胞自动机之一,也许是有史以来最受欢迎的一种,是称为“生命游戏”的二维 CA,简称 GoL。 它由 John H. Conway 开发并于 1970 年在《科学美国人》(Scientific American)的马丁加德纳(Martin Gardner)专栏中推广。 请参阅 http://en.wikipedia.org/wiki/Conway_Game_of_Life。
GoL 中的细胞排列在一个二维网格中,两个方向上都有限,或者首尾相接。 双向首尾相接的网格称为环面,因为它在地形上等同于多纳圈的表面。 见 http://en.wikipedia.org/wiki/Torus。
每个细胞有两个状态 - 生存和死亡 - 和八个邻居 - 东西南北和四个对角线。 这些邻居有时被称为“摩尔邻域”。
就像前面章节中的一维 CA 一样,生命游戏按照规则演变,这就像物理学的简单定律。
在 GoL 中,每个单元格的下一个状态取决于其当前状态和活动邻居的数量。 如果一个细胞是活的,如果它有两个或三个活动邻居就会生存,否则就会死亡。 如果一个细胞是死的,它将保持死亡,除非它恰好有三个邻居。
下表总结了这些规则:
| 当前状态 | 邻居数量 | 下一个状态 |
|---|---|---|
| 生存 | 2–3 | 生存 |
| 生存 | 0–1, 4–8 | 死亡 |
| 死亡 | 3 | 生存 |
| 死亡 | 0–2, 4–8 | 死亡 |
这种行为与真正的细胞生长大致类似:分离或过度拥挤的细胞死亡;它们在中等密度下蓬勃成长。
GoL 很受欢迎,因为:
有简单的初始条件产生令人惊讶的复杂行为。
有许多有趣的稳定图案:有些摆动(以不同的周期),有些像 Wolfram 的 CA 规则 110 中的飞船一样移动。
和规则 110 一样,GoL 是图灵完整的。
另一个产生兴趣的因素是康威的猜测 - 没有可以使活细胞数量无限增长的初始条件 - 以及他向任何可以证明或否定它的人提供的 50 美元赏金。
最后,计算机日益增加的可用性,使得自动化计算并以图形方式显示结果成为可能。
6.2 生命图案
图 6.1:一个静态图案,叫做“蜂巢”(beehive)
图 6.2:一个振荡图案,叫做“蟾蜍”(toad)
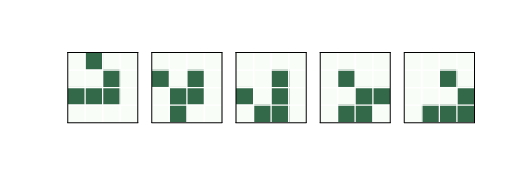
图 6.3:一个飞船,叫做“滑翔机”(glider)
如果从随机起始状态运行 GoL,可能会出现一些稳定图案。随着时间的推移,人们已经确定了这些图案并给了它们名字
例如,图?展示了一种称为“蜂巢”的稳定图案。蜂巢中的每个细胞都有两个或三个邻居,所以它们都能存活下来,蜂巢旁边的死细胞都没有三个邻居,所以没有新细胞诞生。
其他图案在“振荡”;也就是说,它们随着时间而改变,但最终返回到它们的起始状态(只要它们不与另一个图案冲突)。例如,图?展示了一种称为“蟾蜍”的图案,它是在两种状态之间交替的振荡图案。这个振荡图案的“周期”是二。
最后,一些图案振荡并返回到起始状态,但在空间中移动。因为这些图案似乎在移动,所以它们被称为“飞船”。
图?展示了一艘名为“滑翔机”的飞船。经过四段时间后,滑翔机回到起始位置,并向下和向右移动一个单位。
根据起始方向,滑翔机可以沿着四条对角线中的任何一条移动。还有其它的水平和垂直移动的飞船。
人们花费了大量时间来查找和命名这些图案。如果你搜索网页,你会发现很多收藏品。
6.3 Conwey 的推测
从最初的条件来看,GoL 迅速达到稳定状态,活细胞数量几乎不变(可能带有一些振荡)。
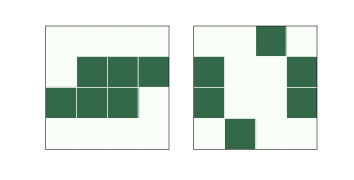
图 6.4:r-pentomino 的开始和最终状态
但是一些简单的开始条件,需要很长时间才能稳定下来,并产生令人惊讶的活细胞数量。 这些模式被称为“Methuselahs”,因为它们很长寿。
其中最简单的是 r-pentomino,它只有五个细胞,形状大致为字母“r”。 图?显示了 r-pentomino 的初始状态和 1103 步后的最终状态。
这种状态是“最终的”,因为所有剩余图案是稳定的,振荡的或滑翔机,它们永远不会与另一种图案相冲突。 r-pentomino 总共产生 6 个滑翔机,8 个积木(block),4 个闪光灯(blinker),4 个蜂巢,1 个小艇(boat),1 个轮船(ship)和 1 个面包(loaf)。
图 6.5:Gosper 的滑翔机枪,产生滑翔机流。
长寿图案的存在,使得康威怀疑是否存在从未稳定的初始图案。 他猜想没有,但他描述了两种证明他是错误的图案,“枪”(gun)和“蒸汽火车”(puffer train)。 枪是稳定的模式,定期产生飞船 - 随着飞船流从源位置移动,活细胞的数量无限增长。 蒸汽火车是一种将活细胞留在尾部的平移图案。
事实证明,这两种模式都存在。 由 Bill Gosper 领导的一个小组发现了第一个,它是现在称为 Gosper’s Gun 的滑翔枪,如图所示。 Gosper 还发现了第一个蒸汽火车。
这两种类型都有很多图案,但它们很难设计或找到。 这不是巧合。 Conway 选择了 GoL 的规则,这样他的猜想就不会明显为真或假。 在二维 CA 的所有可能规则中,大多数产生简单的行为:大多数初始条件快速稳定或无限增长。 通过避免无趣的 CA,Conway 也避免了 Wolfram 的一类和二类行为,并且可能还有三类。
如果我们相信 Wolfram 的计算等价原则,我们预计 GoL 会属于第四类,而且是这样。 生命游戏在 1982 年被证明了图灵的完整性(1983年也是独立的)。 从那时起,几个人构建了 GoL 模式,实现了图灵机或另一台已知图灵完备的机器。
6.4 现实主义
GoL中的稳定模式很难不被注意,特别是那些移动的模式。 将它们视为持久的实体是很自然的事,但请记住,CA 是由细胞构成的;没有蟾蜍或面包这样的东西。 滑翔机和其他飞船甚至更不真实,因为随着时间的推移,它们甚至不由相同的细胞组成。 所以这些图案就像星座一样。 我们这样看待他们,因为我们善于观察图案,或者因为我们有活跃的想象力,但他们不是真实的。
对嘛?
好吧,不是那样。 我们认为“真实”的许多实体,也是规模较小的实体的持久图案。 飓风只是气流的模式,但我们给了他们个人名称。 而人就像滑翔机,随着时间的推移不是由相同细胞组成的。 但即使你更换了你体内的每一个细胞,我们也认为你是同一个人。
这不是一个新观察 - 大约在 2500 年前,赫拉克利特(Heraclitus)指出你不能在同一条河流中两次 - 但是出现在生命游戏中的实体,是思考哲学现实主义的实用测试用例。
在哲学的背景下,现实主义是这样一种观点,即世界中的实体存在与人类的感知和概念无关。 “感知”是指我们从感官中获得的信息,而“概念”是指我们形成的世界的心智模式。 例如,我们的视觉系统将一些东西感知为场景的二维投影,我们的大脑使用该图像构建场景中物体的三维模型。
科学实在论与科学理论和他们所假设的实体有关。 如果一个理论使用实体的属性和行为来表达,那么这个理论假设了一个实体。 例如,电磁学的理论用电场和磁场表示。 经济学的一些理论以供给,需求和市场力量来表达。 生物学的理论是用基因来表达的。
但这些实体是真实的吗? 也就是说,它们存在于独立于我们和我们的理论的世界吗?
再次,我发现,在一系列强度中陈述哲学立场是有用的;这里有四个科学现实主义的陈述,强度逐渐增加:
SR1:
对于它们接近现实的程度,科学理论为真或假,但没有理论是完全正确的。 一些所假设的实体可能是真实的,但没有原则性的方式来说出哪些是真实的。
SR2:
随着科学的进步,我们的理论会变得更加逼近现实。 至少有一些所假定的实体是已知真实的。
SR3:
有些理论是完全正确的;其他近似真实。 真实理论所假设的实体,以及近似真实理论中的一些实体是真实的。
SR4:
如果一个理论正确地描述了现实,那么这个理论就是真的,否则就是假。真实理论所假设的实体是真实的;其他不是。
SR4 非常强,可能是站不住脚的;通过这样一个严格的标准,几乎所有当前的理论都被认为是错误的。 大多数现实主义者会接受 SR1 和 SR3 之间的东西。
6.5 工具主义
但 SR1 很弱以至于它接近工具主义,这是一种观点,我们不能说理论是真是假,因为我们不知道理论是否符合现实。 理论是我们用于我们的目的的工具;在适用于其目的的程度上,理论是有用的,或者不是。
要看看你是否对工具主义感到满意,请考虑以下陈述:
“生命游戏中的实体并不是真实的;他们只是人们赋予可爱的名字的细胞图案。”
“飓风只是一种气流模式,但它是一种有用的描述,因为它可以让我们进行有关天气的预测和沟通。”
“像本我和超我这样的弗洛伊德实体并不是真实的,但它们是思考和交流心理学的有用工具(或者至少有些人是这么认为的)。”
“电磁场是我们最好的电磁理论中的假设实体,但它们并不真实。 我们可以构建其他理论,而不用场的假设,这也是一样有用的。”
“我们认为,世界上的许多物体都是像星座一样的任意集合。 例如,蘑菇只是真菌的子实体,其中大部分是在地下生长的,几乎不连续的细胞网络。 我们由于实际原因专注于蘑菇,如可见性和可爱。”
“有些物体边界清晰,但很多都是模糊的。 例如,哪些分子是你身体的一部分:你的肺里的空气? 你的胃里的食物? 你血液中的营养物质? 细胞中的营养物质? 细胞中的水? 细胞的结构部分? 头发? 死皮? 污垢? 你的皮肤上的细菌? 你的肠道细菌?线粒体? 当你称量自己时,你包含了多少这些分子? 根据离散对象构想世界是有用的,但我们确定的实体并不是真实的。”
对于每一个你同意的陈述,给自己一分。 如果你的分数超过 4 分,你可能会成为一名工具主义者!
如果你比其他人更喜欢这些陈述,那么问问你自己为什么。 这些情景中的哪些差异会影响你的反应? 你能否在他们之间做出原则性区分?
工具主义的更多信息,请参阅 http://en.wikipedia.org/wiki/Instrumentalism。
6.6 实现
本章最后的练习要求你尝试和修改生命游戏,并实现其他二维细胞自动机。 本节介绍 GoL 的实现,你可以将其用作实验的起始位置。
为了表示细胞的状态,我使用类型为uint8的 NumPy 数组,它是一个 8 位无符号整数。 例如,下面这行创建一个 10 乘 10 的数组,并用 0 和 1 的随机值进行初始化。
a = np.random.randint(2, size=(10, 10)).astype(np.uint8)我们可以用几种方法计算 GoL 规则。 最简单的方法是使用for循环遍历数组的行和列:
b = np.zeros_like(a)
rows, cols = a.shape
for i in range(1, rows-1):
for j in range(1, cols-1):
state = a[i, j]
neighbors = a[i-1:i+2, j-1:j+2]
k = np.sum(neighbors) - state
if state:
if k==2 or k==3:
b[i, j] = 1
else:
if k == 3:
b[i, j] = 1最初,b是一个与a大小相同的零数组。 每次循环中,状态是中心细胞的条件,邻居是3×3的邻域。 k是活动邻居的数量(不包括中心细胞)。 嵌套的if语句评估 GoL 规则并相应地激活b中的细胞。
这个实现是规则的直接翻译,但它是冗长而缓慢的。 我们可以使用互相关做得更好,正如我们在第?节中看到的那样。 在那里,我们使用np.correlate来计算一维相关。 现在,为了计算二维相关,我们将使用scipy.signal中的correlate2d,它是一个 SciPy 模块,提供信号处理的相关函数:
from scipy.signal import correlate2d
kernel = np.array([[1, 1, 1],
[1, 0, 1],
[1, 1, 1]])
c = correlate2d(a, kernel, mode='same')在一维相关的背景下,我们称之为“窗口”的内容,在二维相关的背景下被称为“核”,但其想法是相同的:correlate2d将核和数组相乘来选择一个邻域,然后将结果加起来。 这会核选择中心细胞周围的 8 个邻居。
correlate2d将核应用于数组中的每个位置。 使用mode ='same'时,结果与a的大小相同。
现在我们可以使用逻辑运算符来计算规则:
b = (c==3) | (c==2) & a
b = b.astype(np.uint8)第一行计算了一个布尔数组,其中应该有活细胞的地方为True,其他地方为False。 然后,astype将布尔数组转换为整数数组。
这个版本更快,也许够好,但是我们可以通过修改核来简化它:
kernel = np.array([[1, 1, 1],
[1,10, 1],
[1, 1, 1]])
c = correlate2d(a, kernel, mode='same')
b = (c==3) | (c==12) | (c==13)
b = b.astype(np.uint8)这个版本核的包含中心单元并赋予其权重 10。如果中心单元为 0,则结果介于 0 和 8 之间; 如果中心单元为 1,则结果在 10 到 18 之间。使用这个核,我们可以简化逻辑运算,只选择值为 3,12 和 13 的细胞。
这看起来可能不是什么大的改进,但它允许进一步简化:使用这个核,我们可以使用一个表来查找细胞的值,就像我们在第?节中所做的那样。
table = np.zeros(20, dtype=np.uint8)
table[[3, 12, 13]] = 1
c = correlate2d(a, kernel, mode='same')
b = table[c]除了位置 3,12 和 13 以外,表格中的任何位置都为零。当我们使用c作为表格中的索引时,NumPy 执行逐元素查找;也就是说,它从c中获取每个值,在表中查找它并将结果放入b中。
这个版本比其他版本更快更简洁, 唯一的缺点是需要更多的解释。
包含在本书仓库中的Life.py提供了一个封装规则实现的Life类。 如果你执行Life.py,你应该看到一个“蒸汽火车”的动画,这是一种飞船,在其尾部留下一串碎屑。
6.7 练习
练习 1
本章的代码位于本书仓库的 Jupyter 笔记本chap06.ipynb中。 打开这个笔记本,阅读代码,然后运行单元格。 你可以使用这个笔记本来练习本章的练习。 我的解决方案在chap06soln.ipynb中。
练习 2
以随机状态启动 GoL 并运行它直至稳定。 你可以识别哪些稳定的图案?
练习 3
许多命名图案都以便携式文件格式提供。 修改Life.py来解析其中一种格式并初始化网格。
练习 4
一种最长寿的小型图案是“兔子”,它以 9 个活动细胞开始,需要 17 331 个步骤来稳定。 你可以在 http://www.conwaylife.com/wiki/Rabbits 获取各种格式的初始状态。 加载此状态并运行它。
练习 5
在我的实现中,Life类基于一个名为Cell2D的父类,LifeViewer基于Cell2DViewer。 你可以使用这些基类来实现其他二维细胞自动机。
例如,GoL 的一个变体叫做“Highlife”,与 GoL 规则相同,另外还有一条规则:有 6 个邻居的死亡细胞会变活。
编写一个名为Highlife的类,该类继承自Cell2D并实现这个版本的规则。 另外编写一个名为HighlifeViewer的类,该类继承自Cell2DViewer并尝试以不同的方式来展示结果。 作为一个简单的例子,使用不同的颜色表。
Highlife中更有趣的图案之一是复制器(replicator)。 使用add_cells和复制器初始化Highlife并查看它做了什么。
练习 6
如果将图灵机扩展到两个维度,或者将读写头添加到二维 CA,则结果是称为 Turmite 的细胞自动机。由于读写头移动的方式,它以白蚁(termite)命名,但拼写错误是对 Alan Turing 的敬意。
最着名的 Turmite 是 1986 年由 Chris Langton 发现的兰顿的蚂蚁(Langton’s Ant)。请见 http://en.wikipedia.org/wiki/Langton_ant。
蚂蚁(ant)是一个具有四种状态的读写头,你可以将其视为面向东、西、南或北。细胞有两种状态,黑色和白色。
规则很简单。在每个时间步骤中,蚂蚁检查它所在单元格的颜色。如果是黑色,蚂蚁转向右转,将细胞变成白色,并向前移动一个格子。如果细胞是白色的,蚂蚁会向左转,将细胞变成黑色,然后向前移动。
给定一个简单的世界,一组简单的规则,并且只有一个可移动的部分,你可能会期望看到简单的行为 - 但你现在应该更清楚。从所有的白色细胞开始,在进入周期为 104 步的循环之前,兰顿的蚂蚁以看似随机的方式移动超过 10000 步。每个循环后,蚂蚁都会沿对角线平移,因此会留下一条称为“高速路”的踪迹。
编写兰顿的蚂蚁的实现。