计算神经科学（三）

神经元的生物物理特性（二）

Goldman-Hodgkin-Katz方程

Nernst-Planck方程描述了带电离子在水介质中的运动。然而，细胞膜具有厚度并且在通道内可能存在能垒（energy barriers）。 在这种情况下，流过开放通道的离子不遵循能斯特 - 普朗克方程，因此我们必须对该膜内的复杂行为进行建模从而获得整个细胞的通量的真实图像。Goldman，Hodgkin和Katz想出了这个简化的模型，称为恒定场方程。 他们假设
（i）脂质膜上的电场是恒定的，
（ii）膜内符合Nernst-Planck方程，
（iii）离子全部独立移动

令VM为宽度为L的膜上的总电位，并且令V（x）为穿过膜的点x处的电势。 由于电场是恒定的，E = -VM / L。 这意味着dV / dx = VM / L。 膜内离子的迁移率与水溶液中的离子迁移率不同; 用u *表示这种移动性。 最后，令β为膜内离子溶解度与水溶液中溶解度的比率。 因此，如果[C]是含水浓度，那么β[C]是膜浓度。 根据这些假设，穿过膜的电流的Nernst-Planck方程是：

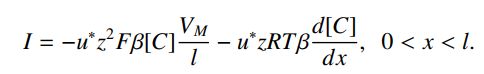
这只是[C]的一阶线性常微分方程，受两个边界条件的影响

通常，不能解决具有两个边界条件的一阶方程。 然而，当前的 I 是未知的，因此正确选择这将允许我们找到满足两个边界条件的解决方案。 结果是：

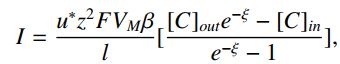
其中，

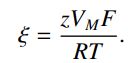
这个表达通常是用渗透率来写的，

综上可得，

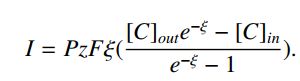
这是由单一离子物质引起的电流。 电流在离子物质的平衡或能斯特电势下消失。绘制的常见量是电流 - 电压（I - V）图。 如果内部和外部浓度相同，那么I - V图是线性的。对于[C] out> [C] in（resp。[C] out <[C] in），I-V图是向下凹的（相应的向上）。电流的大小很大程度上取决于电位是否高于或低于平衡。

根据假设（iii），其假设离子不相互作用，总电流等于各种离子电流之和。假设有三种渗透离子：K +，Na +和Cl-。具有相应的电流，IK，INa和ICl。 在平衡时，总电流I = IK + INa + ICl消失; 也就是说，I = 0。

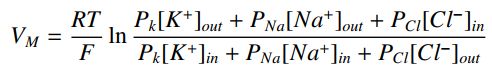
其中P是三种离子物质中每一种的渗透性。 这是上面讨论的能斯特均衡的推广，被称为Goldman-Hodgkin-Katz方程（GHK）。 例如，在鱿鱼轴突中，静息状态下，渗透率的比率是PK：PNa：PCl = 1：0.03：0.1。 细胞内的离子浓度分别为K; Na和Cl; 400mM，50mM和40mM; 而在细胞外，分别是10mM，460mM和540mM。 因此，在室温下，平衡或静息电位为-70mV。

膜电压方程

任何物理或生物物理机制实例化一个需要在现实世界中生存的信息处理系统，都必须遵守以下几个约束:：
（i）它必须以高速运行，
（ii）它必须具有丰富的计算原语库，能够实现各种线性和非线性操作，
（iii）它必须与物理世界有接口——在能够准确表示感知输入模式并将计算结果转化为动作（即电机输出）的意义上。

膜电位是神经系统中满足这三个要求的一个物理变量：它可以在很远的距离内快速变化，膜电位控制着大量的非线性门控- 离子通道 ，这为实现非线性操作提供了非常丰富的基础。这些通道将视觉，触觉，听觉和嗅觉刺激转换为膜电位的变化，并且这种电压变回神经递质的释放或肌肉的收缩。

被动神经元膜的结构

先从单个神经元看，根据之前文章：

其中 t 代表时间。在静止时，所有细胞，无论是神经元、神经胶质细胞还是肌细胞，都具有负静息电位Vrest，其可以高达-30mV或低至-90mV。请注意，当我们说细胞处于“静止”状态时，它实际上处于动态平衡状态，如上所述：离子电流流过膜，但它们相互平衡，使净电流流动穿过膜是零。维持这种平衡是神经系统的主要能量消耗。哺乳动物大脑消耗的代谢能量的一半是由于膜泵引起的，其负责维持离子梯度。

膜电容

作为分离细胞内、外细胞质的细胞膜的性质是什么？生物膜的两个基本组成元素是蛋白质和脂质。膜的骨架由磷脂双分子层组成，我们知道，只要薄绝缘体使得电荷分离，它就可以看成一个电容。膜电位Vm允许膜的两侧形成电荷Q.

在膜生物物理学中，电容通常根据特定膜电容Cm来指定。C的实际值可以通过将Cm乘以总膜面积来获得。半脂层的厚度和介电常数决定了Cm的数值。对于由两个平行板形成的最简单类型的电容，Cm与分隔电荷的厚度成反比（两个板之间的距离越薄，电荷在绝缘材料上的相互吸引越强）。

当电容两端的电压发生变化时，电流就会流动。 通过微分等式获得在电容上移动或移出的电容性电流。

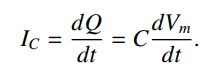
对于固定电流，膜电容的存在限制了Vm响应该电流可以多快地改变; 电容越大，电压变化越慢。

膜上绝对没有任何实际的电荷移动。当电压随时间变化时，电荷会发生变化，电流会流过，但绝不会直接穿过电容。 电荷仅通过电路的其余部分在两侧重新分配。

膜电导

蛋白质分子占膜的20-80％（干重），可提供大量特定的细胞功能，包括离子通道、酶、泵和受体。它们充当脂质屏障中的门或门控，特定信息或物质可通过所述门或门控从一侧转移到另一侧。即存在各种各样的“门”，用不同的key打开它们。目前，我们对那些充当离子通道或么门控的膜蛋白感兴趣，使离子能够从膜的一侧传播到另一侧。现在，我们将通过简单的线性电阻R概括地描述通过这些通道的电流。由于我们还必须考虑细胞的静息电位，因此对一小块膜的最简单的电气描述包括三个元素C、R和Vrest（电容、电导和静息电位’），因此我们称之为RC电路。

简单RC电路

假设我们已经确定了一个直径为d的小球形神经元，并设法将一个小电极插入细胞而不会破坏它。我们想知道如果我们将刺激电流Iin（t）通过微电极直接注入细胞会发生什么。该电极可以被认为是理想的电流源（与理想的电压源相比，例如电池）。

我们如何描述响应该电流的膜电位Vm（t）的动态变化？ 细胞膜可以概念化为由许多小RC电路组成。因为细胞的尺寸很小，所以膜上的电势无处不在，我们可以忽略任何空间依赖性； 这意味着可以通过具有电流源的单个RC电路充分描述电池的电行为。

通过应用基尔霍夫电流定律来描述该电路的动态，该定律指出流入或流出任何电节点的所有电流的总和必须为零（电流不能消失，它必须去某处）。

注意，电阻上的电位不等于Vm，而是等于膜电位和虚拟电池Vrest之间的差异。电容和电阻电流必须等于外部电流或电流

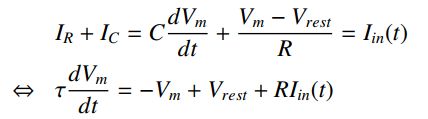
其中τ= RC，单位为ΩF= sec。

按照惯例，向外电流，即从神经元内部流到外部的电荷，表示为正电流。 通过细胞内电极传递的向外电流将使细胞内部更正； 在生理学上称之为细胞是去极化的。 相反，由相同电极提供的向内定向电流（按照惯例在负方向上绘制）将使内部更负，即超极化。 如果电流不是从外部电源施加，而是由膜电导产生，则情况是不同的。

上述方程称为膜方程，构成一阶常微分方程。 在适当的初始条件下，它指定了一个独特的电压轨迹。 让我们假设膜电位在Vm（0）= Vrest时开始。 我们立即看到dVM / dt = 0，没有任何输入电流。

其中V1 = R*I0被定义为响应给定电流的稳态电位。该等式告诉我们，膜电位与其静止状态的偏差的时间过程，即Vm-Vrest，是时间上的指数函数，具有时间常数τ。即使电流瞬间从零变为I0，但膜电位不能跟随，但是会起到作用。 Vm的变化速度由膜电阻和电容的乘积决定;电容越大，充电C的电流越大。

从小鼠海马锥体神经元记录的动作电位（蓝色迹线）。

参考文献

http：//www.answers.com/topic/action-potential-vert-png。