SM3密码算法 - Python实现
接上一篇ZUC密码算法,这一篇是国密SM3算法的实现。此实现基于Python 3.7.1,参考国密局SM3官方文档。官方文档百度文库里有,这里就不放了,省的搞我个侵权什么的。
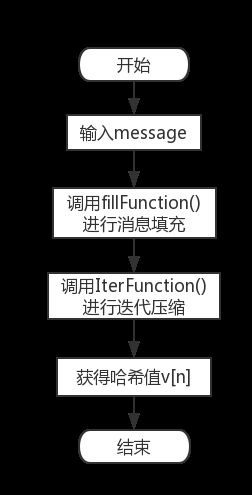
整体上,算法流程如下:
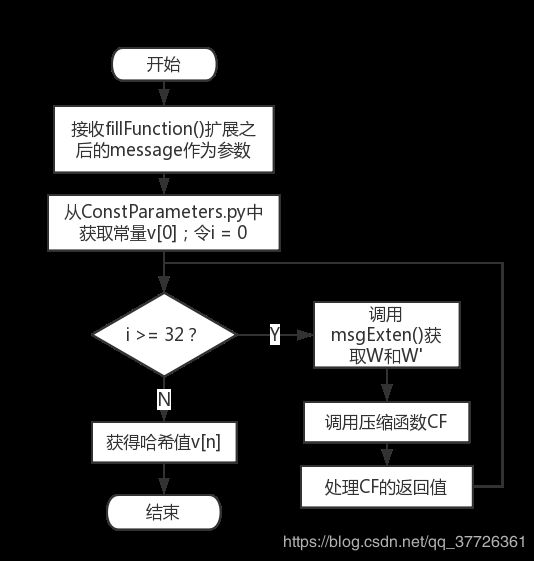
其中,IterFunction函数流程如下:
源码分割为两个文件:ConstParameters.py & Functions.py,前者为常量代码,后者为算法各模块实现。
ConstParamters.py
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 5 20:44:52 2018
@author: wang
"""
vi = 0x7380166f4914b2b9172442d7da8a0600a96f30bc163138aae38dee4db0fb0e4e
t = [0x79cc4519, 0x7a879d8a]Functions.py
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 5 20:45:11 2018
@author: wang
"""
import ConstParameters as cp
MAX = 2**32
'''
convert int to k-bit binary number
input:a-int; k-int;
output:string
'''
def Int2Bin(a, k):
res = list(bin(a)[2:])
for i in range(k-len(res)):
res.insert(0, '0')
return ''.join(res)
'''
loop left shift function
#input:a-int; k-int, the number of bits that should be shift;
#output-int
'''
def LoopLeftShift(a, k):
res = list(Int2Bin(a, 32))
for i in range(k):
temp = res.pop(0)
res.append(temp)
return int(''.join(res), 2)
'''
在官方文档中,填充结果是以十六进制表示的,而一个十六进制位表示四个二进制位,
因而在将输入的message转换为0/1字符串后,要检查是否需要在字符串顶端补零,
以确保其长度等于(message的十六进制字符串长度)*4。
input:message-int
output:message-a string consisited by '0'/'1'
'''
def fillFunction(message):
message = bin(message)[2:]
for i in range(4):
if (len(message)%4 == 0):
break
else:
message = '0'+message
length = len(message)
k = 448 - (length+1)%512
if (k < 0): #k是满足等式的最小非负整数
k += 512
addMessage = '1' + '0'*k + Int2Bin(length, 64)
message += addMessage
return message
def IterFunction(message):
n = int(len(message)/512)
v = []
v.append(Int2Bin(cp.vi, 256))
for i in range(n):
w, w1 = msgExten(message[512*i:512*(i+1)])
temp = CF(v[i], message[512*i:512*(i+1)], w, w1)
temp = Int2Bin(temp, 256)
v.append(temp)
return v[n]
'''
消息扩展函数
b-int
w, w1即官网文档中的W和W',数据类型为list
'''
def msgExten(b):
w = []
w1 = []
for i in range(16):
temp = b[i*32:(i+1)*32]
w.append(int(temp, 2))
for j in range(16, 68, 1):
factor1 = LoopLeftShift(w[j-3], 15)
factor2 = LoopLeftShift(w[j-13], 7)
factor3 = P1(w[j-16]^w[j-9]^factor1)
factor4 = factor3^factor2^w[j-6]
w.append(factor4)
for j in range(64):
factor1 = w[j]^w[j+4]
w1.append(factor1)
return w, w1
'''
官方文档中同名的一些小函数
'''
def P0(X):
return X^LoopLeftShift(X, 9)^LoopLeftShift(X, 17)
def P1(X):
return X^LoopLeftShift(X, 15)^LoopLeftShift(X, 23)
def T(j):
if j <= 15:
return cp.t[0]
else:
return cp.t[1]
def FF(X, Y, Z, j):
if j <= 15:
return X^Y^Z
else:
return (X&Y)|(X&Z)|(Y&Z)
def GG(X, Y, Z, j):
if j <= 15:
return X^Y^Z
else:
return (X&Y)|(un(X)&Z)
'''
Python的~是补码非,因而得自己写个32位二进制非运算
input:a-int
output:int
'''
def un(a):
a = Int2Bin(a, 32)
b = ''
for i in a:
if i == '0':
b += '1'
else:
b+= '0'
return int(b, 2)
'''
压缩函数CF
vi-
'''
def CF(vi, bi, w, w1):
A = []
for i in range(8):
temp = vi[32*i:32*(i+1)]
A.append(int(temp, 2))
for j in range(64):
factor1 = LoopLeftShift(A[0], 12)
factor2 = LoopLeftShift(T(j), j%32)
SS1 = LoopLeftShift((factor1+A[4]+factor2)%MAX, 7)
factor3 = LoopLeftShift(A[0], 12)
SS2 = SS1^factor3
TT1 = (FF(A[0], A[1], A[2], j) + A[3] + SS2 + w1[j])%MAX
TT2 = (GG(A[4], A[5], A[6], j) + A[7] + SS1 + w[j])%MAX
A[3] = A[2]
A[2] = LoopLeftShift(A[1], 9)
A[1] = A[0]
A[0] = TT1
A[7] = A[6]
A[6] = LoopLeftShift(A[5], 19)
A[5] = A[4]
A[4] = P0(TT2)
temp = Int2Bin(A[0], 32)+Int2Bin(A[1], 32)+Int2Bin(A[2], 32)+\
Int2Bin(A[3], 32)+Int2Bin(A[4], 32)+Int2Bin(A[5], 32)+\
Int2Bin(A[6], 32)+Int2Bin(A[7], 32)
temp = int(temp, 2)
return temp^int(vi, 2)
算法各模块测试:
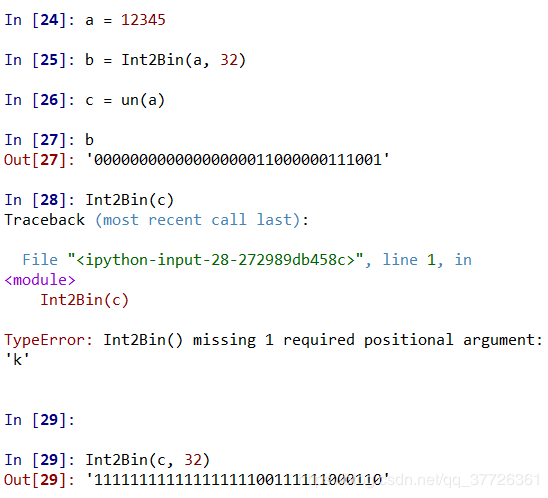
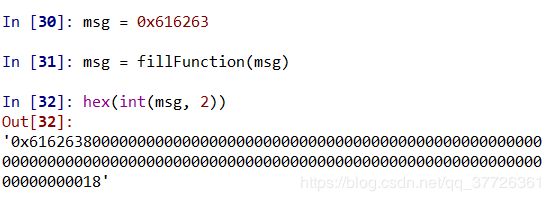
| 原码非: 参数a是整型,接收参数后先将其转换为32位0/1字符串,然后扫描整个字符串,进行非运算。 消息填充函数fillFunction(): 需要注意,在官方文档中,填充结果是以十六进制表示的,而一个十六进制位表示四个二进制位,因而在将输入的message转换为0/1字符串后,要检查是否需要在字符串顶端补零,以确保其长度等于(message的十六进制字符串长度)*4。 数字转二进制字符串模块Int2Bin()、循环左移模块LoopLeftShift()与前两个实验中的完全相同,我不再赘述。 其他模块就按官方文档写就好,没有什么特别需要注意的地方。 |
算法整体测试:
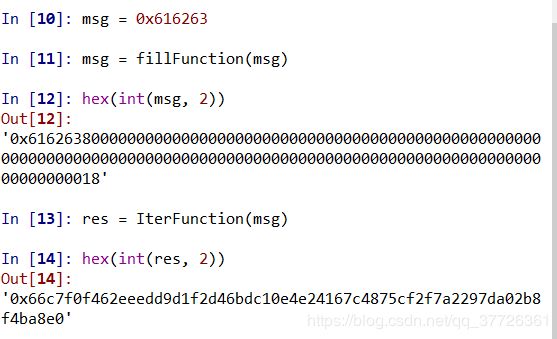
| 输入message=0x616263,即官方文旦中第一个测试样例: 结果与官方文档中的一致。
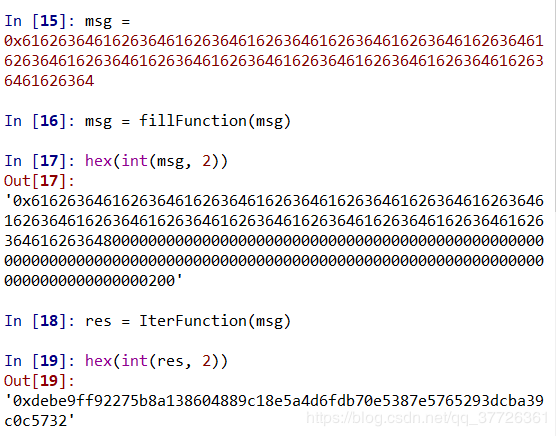
官方文档中第二个样例,输入数据为0x61626364616263646162636461626364616263646162636461626364616263646162636461626364616263646162636461626364616263646162636461626364,运行结果如下: 与官方文档中一致。 |
| Int2Bin()、LoopLeftShift在之前的实验中已经测试过,这里着重测试原码非模块、消息扩展模块、迭代压缩CF模块。 原码非un():输入数据a=12345。 消息填充函数fillFunction():输入数据msg=0x616263 与官方文档中一致。
消息扩展函数msgExten():输入数据message=fillFunction(0x616263) 其输出结果与官方文档中一致。 消息压缩函数CF(): 与官方文档中一致。 其他的细小功能模块,如P0、P1之类,非常简单,这里不再单独测试。 |