06 第三章、趣味盎然
文章目录
- 第 3 章、趣味盎然
- 3.1、自己的手写数字
- 3.2、神经网络大脑内部
- 3.2.1、神秘的黑盒子
- 3.2.2、向后查询
- 3.2.3、标签“0”
- 3.2.4、更多的大脑扫描
- 3.3、创建新的训练数据:旋转图像
- 3.4、结语
第 3 章、趣味盎然
3.1、自己的手写数字
1、制作图片
第一种方式:自己手写,然后拍照,然后对照片进行旋转和剪裁处理,最后修改照片大小和像素,使之成为2828的,最后转换格式成JPG或者PNG的。
第二种方式,直接用windows自带的画板程绘图,然后修改照片大小和像素,使之成为2828的,最后另存为JPG或者PNG的即可。
刚开始我用的第一种方式,因为光照等不同,噪声比较多,基本没有什么识别成功的。后来经过观察发现原先的MNIST数据集的空白部分都是0,所以,都是去噪声的,经过把空白部分人为的涂白后,效果不佳,且浪费时间,最后直接用绘图软件制作,识别率才转向正常,识别率0.7,还可以吧,因为毕竟鼠标写的和手写的还是有点区别的。
2、将图片转换成可以处理的数据
第一步,用python的画图工具,看看读入的文件经过第一步处理后还是不是正常的图片,主要看scipy.misc.imread函数是否起作用。
# 将自己制作的图片转换成csv可以用的格式
import scipy.misc
import numpy
import matplotlib.pyplot
image_file_name = "D:\\vsc_pro\\CNN\\data\\3\\0.png"
img_array = scipy.misc.imread(image_file_name, flatten=True)
img_data = 255.0-img_array.reshape(784)
img_array = img_data.reshape((28, 28))
# img_data = (img_data/255.0*0.99)+0.01
print(img_array)
# 绘制数组,第一个参数是数组,第二个参数是绘制方式,Greys是灰度调色板
matplotlib.pyplot.imshow(img_array, cmap='Greys', interpolation='None')
# 显示上面的画的图像
matplotlib.pyplot.show()
3、将图片数据加上lable然后放入csv文件中
# 将自己制作的图片转换成csv可以用的格式
import scipy.misc
import numpy
import matplotlib.pyplot
import os
# 获取文件路径,文件名,文件后缀
def get_filePath_fileName_fileExt(filename):
(filepath, tempfilename) = os.path.split(filename)
(shotname, extension) = os.path.splitext(tempfilename)
return filepath, shotname, extension
# 定义文件路径
image_file_name = "D:\\vsc_pro\\CNN\\data\\3\\5.png"
# 从常见的图像文件格式(包括PNG和JPG)中读取和解码数据
# flatten是是否将图片变成简单的浮点数组,如果图片是彩色的,就转换成灰度
img_data_temp = scipy.misc.imread(image_file_name, flatten=True)
# 常规而言,0是黑色,255是白色,但是MNIST数据集用相反的方式表示,所以要逆转过来
img_data = 255.0-img_data_temp
# 将从文件中读出的28*28的数据变成一行784个数
img_array = img_data.reshape(784)
# 将数据转换成list,因为list是可变长度的,才能insert,numpy的list都是固定长度的
img_array = img_array.tolist()
# 获取文件路径,文件名,文件后缀
file_path, file_name, file_ext = get_filePath_fileName_fileExt(image_file_name)
# 给数据添加标签
img_array.insert(0, int(file_name))
# 把数据转换成numpy的list,因为下面的savatxt的参数是numpy的list
file_array = numpy.array(img_array)
# 写文件,savetxt是numpy提供的函数,第一个参数是文件名,第二个参数是写入的内容
# 第三个参数是对写入的内容进行分割,第四个参数是一行多长,第五个是用什么分隔每行
numpy.savetxt("data.csv", file_array, delimiter=',', fmt=[
'%s']*file_array.shape[1], newline='\n')
4、将多个自己制作的图片写入到一个csv文件中,因为numpy提供的savatxt不能追加数据,而普通的open函数使用参数‘a’虽然可以追加,但是成格式地写入csv却很麻烦,所以我现试试两个图片的输入,但是图片多了会不会造成一个数组太大,内存不够的情况,之后再解决吧,代码如下
# 将自己制作的多个图片转换成csv可以用的格式
import scipy.misc
import numpy
import matplotlib.pyplot
import os
# 获取文件路径,文件名,文件后缀
def get_filePath_fileName_fileExt(filename):
(filepath, tempfilename) = os.path.split(filename)
(shotname, extension) = os.path.splitext(tempfilename)
return filepath, shotname, extension
# 存放写入文件的内容
file_array = []
# 定义文件路径
image_file_name = "D:\\vsc_pro\\CNN\\data\\3\\3.png"
# 从常见的图像文件格式(包括PNG和JPG)中读取和解码数据
# flatten是是否将图片变成简单的浮点数组,如果图片是彩色的,就转换成灰度
img_data_temp = scipy.misc.imread(image_file_name, flatten=True)
# 常规而言,0是黑色,255是白色,但是MNIST数据集用相反的方式表示,所以要逆转过来
img_data = 255.0-img_data_temp
# 将从文件中读出的28*28的数据变成一行784个数
img_array = img_data.reshape(784)
# 将数据转换成list,因为list是可变长度的,才能insert,numpy的list都是固定长度的
img_array = img_array.tolist()
# 获取文件路径,文件名,文件后缀
file_path, file_name, file_ext = get_filePath_fileName_fileExt(image_file_name)
# 给数据添加标签
img_array.insert(0, int(file_name))
# 添加一个数据
file_array.append(img_array)
# 定义文件路径
image_file_name = "D:\\vsc_pro\\CNN\\data\\3\\5.png"
# 从常见的图像文件格式(包括PNG和JPG)中读取和解码数据
# flatten是是否将图片变成简单的浮点数组,如果图片是彩色的,就转换成灰度
img_data_temp = scipy.misc.imread(image_file_name, flatten=True)
# 常规而言,0是黑色,255是白色,但是MNIST数据集用相反的方式表示,所以要逆转过来
img_data = 255.0-img_data_temp
# 将从文件中读出的28*28的数据变成一行784个数
img_array = img_data.reshape(784)
# 将数据转换成list,因为list是可变长度的,才能insert,numpy的list都是固定长度的
img_array = img_array.tolist()
# 获取文件路径,文件名,文件后缀
file_path, file_name, file_ext = get_filePath_fileName_fileExt(image_file_name)
# 给数据添加标签
img_array.insert(0, int(file_name))
# 添加一个数据
file_array.append(img_array)
print(file_array)
# 把数据转换成numpy的list,因为下面的savatxt的参数是numpy的list
file_array = numpy.array(file_array)
# 写文件,savetxt是numpy提供的函数,第一个参数是文件名,第二个参数是写入的内容
# 第三个参数是对写入的内容进行分割,第四个参数是一行多长,第五个是用什么分隔每行
numpy.savetxt("data.csv", file_array, delimiter=',', fmt=[
'%s']*file_array.shape[1], newline='\n')
5、将整个一个文件夹中的数据存入一个csv文件中:
# 将自己制作的图片放到文件夹中统一转换成csv可以用的格式
import os
import scipy.misc
import numpy
import matplotlib.pyplot
# 这里放着你要操作的文件夹名称
path = "D:\\vsc_pro\\CNN\\data\\5\\"
# 把D:\\vsc_pro\\CNN\\data\\3\\目录下的文件名全部获取保存在files中
files = os.listdir(path)
# 存放写入文件的内容
file_array = []
for file in files:
# 从常见的图像文件格式(包括PNG和JPG)中读取和解码数据
# flatten是是否将图片变成简单的浮点数组,如果图片是彩色的,就转换成灰度
img_data_temp = scipy.misc.imread(path+file, flatten=True)
# 常规而言,0是黑色,255是白色,但是MNIST数据集用相反的方式表示,所以要逆转过来
img_data = 255.0-img_data_temp
# 将从文件中读出的28*28的数据变成一行784个数
img_array = img_data.reshape(784)
# 将数据转换成list,因为list是可变长度的,才能insert,numpy的list都是固定长度的
img_array = img_array.tolist()
# 获取文件路径,文件名,文件后缀
file_name, file_ext = os.path.splitext(file)
# 给数据添加标签
img_array.insert(0, int(file_name))
# 添加一个数据
file_array.append(img_array)
print(file_array)
# 把数据转换成numpy的list,因为下面的savatxt的参数是numpy的list
file_array = numpy.array(file_array)
# 写文件,savetxt是numpy提供的函数,第一个参数是文件名,第二个参数是写入的内容
# 第三个参数是对写入的内容进行分割,第四个参数是一行多长,第五个是用什么分隔每行
numpy.savetxt("data.csv", file_array, delimiter=',', fmt=[
'%s']*file_array.shape[1], newline='\n')
6、书上作者提供的读取PNG文件的代码
# 书上作者提供的读取PNG文件的代码
# helper to load data from PNG image files
# imageio模块可以用于图片的读写
import imageio
# glob helps select multiple files using patterns
# glob模块可以查找符合特定规则的文件路径名。
import glob
import numpy
import matplotlib.pyplot
# our own image test data set
# 存放写入文件的内容
our_own_dataset = []
# 读入每个文件,从一个模糊匹配的文件名中查找,应该是glob专有
for image_file_name in glob.glob('D:\\vsc_pro\\CNN\\data\\5\\?.png'):
# 输出一行提示
print("loading ... ", image_file_name)
# use the filename to set the correct label
# 提取标签
label = int(image_file_name[-5:-4])
# load image data from png files into an array
# 使用imageio模块的imread函数,第一个是文件名,第二个是设置灰度
img_array = imageio.imread(image_file_name, as_gray=True)
# reshape from 28x28 to list of 784 values, invert values
# 常规而言,0是黑色,255是白色,但是MNIST数据集用相反的方式表示,所以要逆转过来
# 将从文件中读出的28*28的数据变成一行784个数
img_data = 255.0 - img_array.reshape(784)
# then scale data to range from 0.01 to 1.0
# 转变成需要的输入,这个我在训练函数和测试函数中写了
img_data = (img_data / 255.0 * 0.99) + 0.01
# 输出最大值和最小值,用于提示
print(numpy.min(img_data))
print(numpy.max(img_data))
# append label and image data to test data set
# 把标签和内容连接起来,numpy的append函数,numpy不能改变长度,所以只好两个一起连
record = numpy.append(label, img_data)
# 输出当前记录
print(record)
# 连接到总共的数据中
our_own_dataset.append(record)
pass
matplotlib.pyplot.imshow(our_own_dataset[3][1:].reshape(
28, 28), cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
print(our_own_dataset[3])
7、用自己写的图片的数组进行测试
我自己制作了两组测试数据,最后的准确率都是0.7,第一次是4,5,9三个识别失败,第二次是4,8,9三个识别失败,自我感觉是我自己手写的和训练图片的位置不太一样的问题。
作者写的这部分的代码和我写的也差不多,这里就不贴他的了。
# 用自己写的图片的数据进行测试
# make your own neural network
# code for a 3-layer neural network, and code for learning the MNIST dataset
import numpy
# scipy.special for the sigmoid function expit()
import scipy.special
# library for plotting arrays
import matplotlib.pyplot
# 这个用于判读文件是否存在
import os
# neural network class definition
class neuralNetwork:
# initialise the neural network
# 初始化神经网络
# inputnodes,hiddennodes,outputnodes分别是输入层,隐藏层和输出层网络节点的个数
# learningrate是学习率
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# set number of nodes in each input, hidden, output layer
# 设置输入,隐藏和输出层节点的数量
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# link weight matrices, wih an who
# 链接权重矩阵
# wih是输入层和隐藏层之间的链接权重矩阵W_input_hidden
# who是输入层和隐藏层之间的链接权重矩阵W_hidden_output
# weights inside the arrays are w_i_j, where link is from node i to node j in the next layer
# 数组里的权重是wij,其中链接是从节点i到节点j的下一层
# numpy.random.normal(a,b,(X,Y))的意思是生成一个随机数组,数组大小为X*Y,内容服从中心值为a,方差为b
# 如果有存入文件的权值,就使用,否自初始化一个
if os.access("wih.csv", os.F_OK):
self.wih = numpy.loadtxt(
open("wih.csv", "rb"), delimiter=",", skiprows=0)
else:
self.wih = numpy.random.normal(
0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
if os.access("who.csv", os.F_OK):
self.who = numpy.loadtxt(
open("who.csv", "rb"), delimiter=",", skiprows=0)
else:
self.who = numpy.random.normal(
0.0, pow(self.inodes, -0.5), (self.onodes, self.hnodes))
# learning rate
# 设置学习率
self.lr = learningrate
# activation function is the sigmod function
self.activation_function = lambda x: scipy.special.expit(x)
pass
# train the neural network
def train(self, inputs_list, targets_list):
# vonvert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
targets = numpy.array(targets_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入
# numpy.dot(X,Y)的意思是两个数组的点乘
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
# 计算输出层的输出
final_outputs = self.activation_function(final_inputs)
# output layer error is the (target-actual)
# 计算输出层的误差
output_error = targets-final_outputs
# hidden layer error is the output_error, split by weight,recombined at hidden nodes
# 计算隐藏层的误差
hidden_error = numpy.dot(self.who.T, output_error)
# update the weights for the links between the hidden and output layers
# 更新隐藏层到输出层的权重
# 下面行末尾加的反斜杠\的意思是编译的时候忽略换行符
# 如果一行写不下,在代码末尾加上“\”即可
# 另外,在括号() {} [] 中的代码不需要换行符“\”,直接换行即可达到同样的效果
self.who += self.lr * \
numpy.dot((output_error*final_outputs*(1.0-final_outputs)),
numpy.transpose(hidden_outputs))
# update the weights for the links between the input and hidden layers
# 更新输入层到隐藏层的权重
self.wih += self.lr * \
numpy.dot((hidden_error*hidden_outputs *
(1.0-hidden_outputs)), numpy.transpose(inputs))
pass
# query the neural network
def query(self, inputs_list):
# convert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入
# numpy.dot(X,Y)的意思是两个数组的点乘
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
# 计算输出层的输出
final_outputs = self.activation_function(final_inputs)
return final_outputs
# number of input, hidden and output nodes
# 设置输入,隐藏和输出层节点的数量
# 输出层有28*28=784个数据
input_nodes = 784
# 这个自己随便设的
hidden_nodes = 200
# 按本例子的的方案,输出有10中,结点有10个
output_nodes = 10
# learning rate is 0.3
# 设置学习率为0.3
learning_rate = 0.2
# create instance of neural network
# 创建一个神经网络的实例
n = neuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
# 测试部分代码
# load the mnist test data CSV file into a list
# 读测试数据文件
test_data_file = open("data.csv", 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()
no = 0
# test the neural network
# scorecard for how well the network perform, initially empty
scorecard = []
# go through all the records in the test data set
for record in test_data_list:
# split the record by the ',' commas
all_values = record.split(',')
# correct answer is first value
correct_label = float(all_values[0])
correct_label = int(correct_label)
# print(correct_label, "correct label")
# scale and shift the inputs
inputs = (numpy.asfarray(all_values[1:])/255.0*0.99)+0.01
# query the network
outputs = n.query(inputs)
# the index of the highest value corresponds to the label
label = numpy.argmax(outputs)
# print(label, "network's answer")
# append correct or incorrect to list
if (label == correct_label):
# network's answer matches correct answer, add 1 to scorecard
scorecard.append(1)
else:
# network's answer doesn't match correct answer, add O to scorecard
scorecard.append(0)
print("第"+str(no)+"号不对")
print(correct_label, "correct label")
print(label, "network's answer")
image_array = numpy.asfarray(all_values[1:]).reshape((28, 28))
matplotlib.pyplot.imshow(
image_array, cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
pass
no += 1
pass
# calculate the performance score, the fraction of correct answers
scorecard_array = numpy.asarray(scorecard)
print("performance = ", scorecard_array.sum()/scorecard_array.size)
3.2、神经网络大脑内部
3.2.1、神秘的黑盒子
神经网络就想一个神秘的黑盒子,虽然经过训练就学会了如何求解问题,但是其所学习的知识常常不能转化为对问题的理解和智慧。
特别是,神经网络的工作方式是将学习分布到不同的链接权重中,这种方式使得神经网络对损坏具有了弹性,这就像生物大脑的运行方式,删除一个节点甚至相当多的节点,都不太可能彻底破坏神经网络良好的工作能力。
3.2.2、向后查询
既然是算法,可以计算的方法,那么只要已知充足,那么就能计算。
既然可以从前往后算,那么当然可以从后往前算。
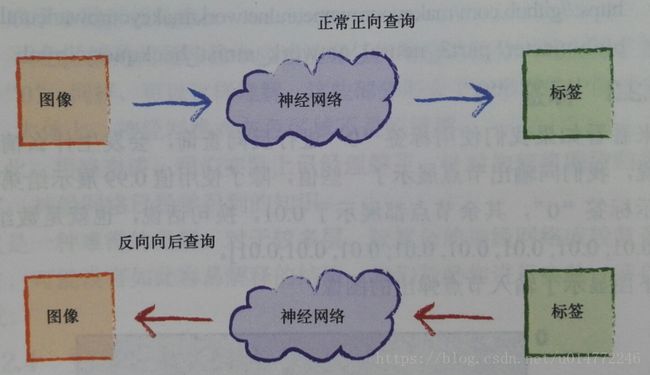
向后查询的逻辑主要由两部分组成:
1、把sigmod函数反写:
self.inverse_activation_function = lambda x: scipy.special.logit(x)
应该放到初始化函数中。
2、反向查询的逻辑,backquery函数
# backquery the neural network
# 反向向后查询函数
def backquery(self, targets_list):
# transpose the targets list to a vertical array
# 获取输出层的输出,这里的输入本来就是标准的0.01到0.99,所以不需要调整
final_outputs = numpy.array(targets_list, ndmin=2).T
# calculate the signal into the final output layer
# 通过反向sigmod函数获取输出层的输入
final_inputs = self.inverse_activation_function(final_outputs)
# calculate the signal out of the hidden layer
# 通过和链接权值计算,得到隐藏层的输出
hidden_outputs = numpy.dot(self.who.T, final_inputs)
# scale them back to 0.01 to 0.99
# 将输出调整到有效的范围,即0.01到0.99,才能用反向sigmod函数,得到sigmod函数的输入
hidden_outputs -= numpy.min(hidden_outputs)
hidden_outputs /= numpy.max(hidden_outputs)
hidden_outputs *= 0.98
hidden_outputs += 0.01
# calculate the signal into the hidden layer
# 通过反向sigmod函数得到隐藏层的输入
hidden_inputs = self.inverse_activation_function(hidden_outputs)
# calculate the signal out of the input layer
# 通过和链接计算,得到输入层的输出
inputs = numpy.dot(self.wih.T, hidden_inputs)
# scale them back to 0.01 to 0.99
# 将输出调整到有效的范围,即0.01到0.99,才是反向sigmod函数,得到sigmod函数的输入
inputs -= numpy.min(inputs)
inputs /= numpy.max(inputs)
inputs *= 0.98
inputs += 0.01
return inputs
3.2.3、标签“0”
接下来把上面的理论和代码综合到整体的代码中,即作者给的代码:
import numpy
# scipy.special for the sigmoid function expit(), and its inverse logit()
import scipy.special
# library for plotting arrays
import matplotlib.pyplot
# neural network class definition
class neuralNetwork:
# initialise the neural network
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# set number of nodes in each input, hidden, output layer
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# link weight matrices, wih and who
# weights inside the arrays are w_i_j, where link is from node i to node j in the next layer
# w11 w21
# w12 w22 etc
self.wih = numpy.random.normal(0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
self.who = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.onodes, self.hnodes))
# learning rate
self.lr = learningrate
# activation function is the sigmoid function
self.activation_function = lambda x: scipy.special.expit(x)
self.inverse_activation_function = lambda x: scipy.special.logit(x)
pass
# train the neural network
def train(self, inputs_list, targets_list):
# convert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
targets = numpy.array(targets_list, ndmin=2).T
# calculate signals into hidden layer
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
final_outputs = self.activation_function(final_inputs)
# output layer error is the (target - actual)
output_errors = targets - final_outputs
# hidden layer error is the output_errors, split by weights, recombined at hidden nodes
hidden_errors = numpy.dot(self.who.T, output_errors)
# update the weights for the links between the hidden and output layers
self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs))
# update the weights for the links between the input and hidden layers
self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs))
pass
# query the neural network
def query(self, inputs_list):
# convert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
# calculate signals into hidden layer
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
final_outputs = self.activation_function(final_inputs)
return final_outputs
# backquery the neural network
# we'll use the same termnimology to each item,
# eg target are the values at the right of the network, albeit used as input
# eg hidden_output is the signal to the right of the middle nodes
def backquery(self, targets_list):
# transpose the targets list to a vertical array
final_outputs = numpy.array(targets_list, ndmin=2).T
# calculate the signal into the final output layer
final_inputs = self.inverse_activation_function(final_outputs)
# calculate the signal out of the hidden layer
hidden_outputs = numpy.dot(self.who.T, final_inputs)
# scale them back to 0.01 to .99
hidden_outputs -= numpy.min(hidden_outputs)
hidden_outputs /= numpy.max(hidden_outputs)
hidden_outputs *= 0.98
hidden_outputs += 0.01
# calculate the signal into the hidden layer
hidden_inputs = self.inverse_activation_function(hidden_outputs)
# calculate the signal out of the input layer
inputs = numpy.dot(self.wih.T, hidden_inputs)
# scale them back to 0.01 to .99
inputs -= numpy.min(inputs)
inputs /= numpy.max(inputs)
inputs *= 0.98
inputs += 0.01
return inputs
# number of input, hidden and output nodes
input_nodes = 784
hidden_nodes = 200
output_nodes = 10
# learning rate
learning_rate = 0.1
# create instance of neural network
n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate)
# load the mnist training data CSV file into a list
training_data_file = open("mnist_dataset/mnist_train.csv", 'r')
training_data_list = training_data_file.readlines()
training_data_file.close()
# train the neural network
# epochs is the number of times the training data set is used for training
epochs = 5
for e in range(epochs):
# go through all records in the training data set
for record in training_data_list:
# split the record by the ',' commas
all_values = record.split(',')
# scale and shift the inputs
inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
# create the target output values (all 0.01, except the desired label which is 0.99)
targets = numpy.zeros(output_nodes) + 0.01
# all_values[0] is the target label for this record
targets[int(all_values[0])] = 0.99
n.train(inputs, targets)
pass
pass
# load the mnist test data CSV file into a list
test_data_file = open("mnist_dataset/mnist_test.csv", 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()
# test the neural network
# scorecard for how well the network performs, initially empty
scorecard = []
# go through all the records in the test data set
for record in test_data_list:
# split the record by the ',' commas
all_values = record.split(',')
# correct answer is first value
correct_label = int(all_values[0])
# scale and shift the inputs
inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
# query the network
outputs = n.query(inputs)
# the index of the highest value corresponds to the label
label = numpy.argmax(outputs)
# append correct or incorrect to list
if (label == correct_label):
# network's answer matches correct answer, add 1 to scorecard
scorecard.append(1)
else:
# network's answer doesn't match correct answer, add 0 to scorecard
scorecard.append(0)
pass
pass
# calculate the performance score, the fraction of correct answers
scorecard_array = numpy.asarray(scorecard)
print ("performance = ", scorecard_array.sum() / scorecard_array.size)
# run the network backwards, given a label, see what image it produces
# label to test
label = 0
# create the output signals for this label
targets = numpy.zeros(output_nodes) + 0.01
# all_values[0] is the target label for this record
targets[label] = 0.99
print(targets)
# get image data
image_data = n.backquery(targets)
# plot image data
matplotlib.pyplot.imshow(image_data.reshape(28,28), cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
结果如下所示:
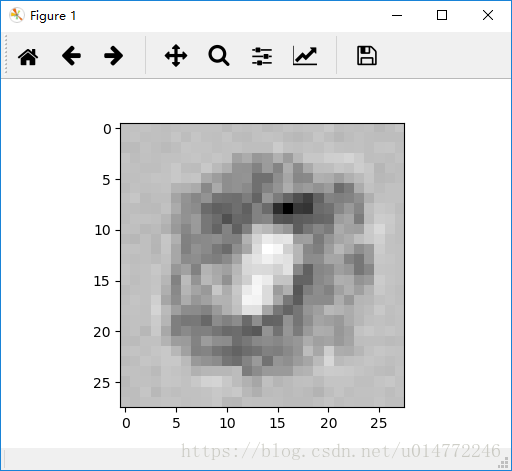
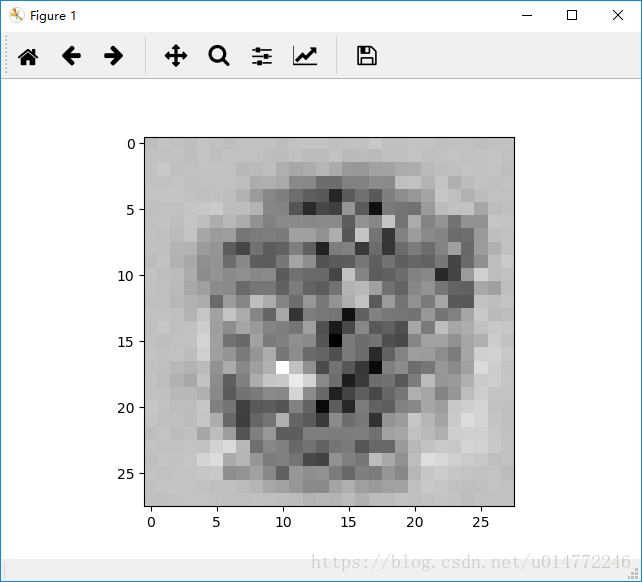
这个是计算0的,输出是[0.99,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01],根据链接权重数组进行计算,书上作者得到的28*28的矩阵变成图片表示为:
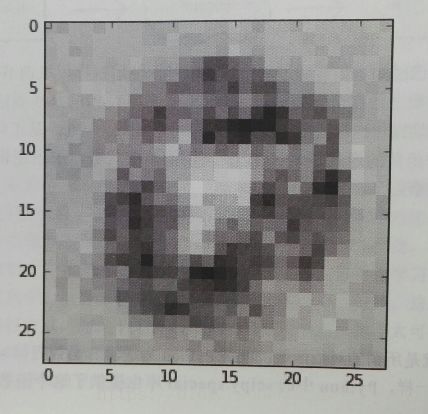
相差不大!
3.2.4、更多的大脑扫描
作者给的代码是重新训练出链接权重,然后进行反向向后查询的。
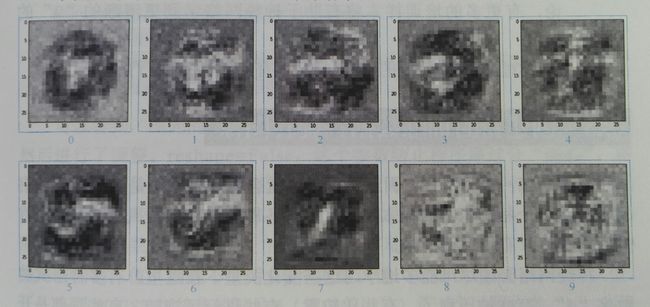
我之前的代码是改进过的,不需要重复训练,可以从已经之前存的权重文件中直接提取权重,所以,我重新写了个代码,去掉了训练部分和查询部分的,直接进行反向向后查询,而且,做了个驯化,让10种输出的数字一个一个的结果都显示出来,代码如下:
# 自己改进的反向向后查询
import numpy
# scipy.special for the sigmoid function expit(), and its inverse logit()
import scipy.special
# library for plotting arrays
import matplotlib.pyplot
# 这个用于判读文件是否存在
import os
# neural network class definition
class neuralNetwork:
# initialise the neural network
# 初始化神经网络
# inputnodes,hiddennodes,outputnodes分别是输入层,隐藏层和输出层网络节点的个数
# learningrate是学习率
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# set number of nodes in each input, hidden, output layer
# 设置输入,隐藏和输出层节点的数量
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# link weight matrices, wih an who
# 链接权重矩阵
# wih是输入层和隐藏层之间的链接权重矩阵W_input_hidden
# who是输入层和隐藏层之间的链接权重矩阵W_hidden_output
# weights inside the arrays are w_i_j, where link is from node i to node j in the next layer
# 数组里的权重是wij,其中链接是从节点i到节点j的下一层
# w11 w21
# numpy.random.normal(a,b,(X,Y))的意思是生成一个随机数组,数组大小为X*Y,内容服从中心值为a,方差为b
# 如果有存入文件的权值,就使用,否自初始化一个
if os.access("wih.csv", os.F_OK):
self.wih = numpy.loadtxt(
open("wih.csv", "rb"), delimiter=",", skiprows=0)
else:
self.wih = numpy.random.normal(
0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
if os.access("who.csv", os.F_OK):
self.who = numpy.loadtxt(
open("who.csv", "rb"), delimiter=",", skiprows=0)
else:
self.who = numpy.random.normal(
0.0, pow(self.inodes, -0.5), (self.onodes, self.hnodes))
# learning rate
# 设置学习率
self.lr = learningrate
# activation function is the sigmod function
# 激活函数的逻辑,expit应该就是sigmod
self.activation_function = lambda x: scipy.special.expit(x)
# 逆激活函数的逻辑,logit应该计算sigmod的反函数
self.inverse_activation_function = lambda x: scipy.special.logit(x)
pass
# train the neural network
def train(self, inputs_list, targets_list):
# vonvert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
targets = numpy.array(targets_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入
# numpy.dot(X,Y)的意思是两个数组的点乘
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
# 计算输出层的输出
final_outputs = self.activation_function(final_inputs)
# output layer error is the (target-actual)
# 计算输出层的误差
output_error = targets-final_outputs
# hidden layer error is the output_error, split by weight,recombined at hidden nodes
# 计算隐藏层的误差
hidden_error = numpy.dot(self.who.T, output_error)
# update the weights for the links between the hidden and output layers
# 更新隐藏层到输出层的权重
# 下面行末尾加的反斜杠\的意思是编译的时候忽略换行符
# 如果一行写不下,在代码末尾加上“\”即可
# 另外,在括号() {} [] 中的代码不需要换行符“\”,直接换行即可达到同样的效果
self.who += self.lr * \
numpy.dot((output_error*final_outputs*(1.0-final_outputs)),
numpy.transpose(hidden_outputs))
# update the weights for the links between the input and hidden layers
# 更新输入层到隐藏层的权重
self.wih += self.lr * \
numpy.dot((hidden_error*hidden_outputs *
(1.0-hidden_outputs)), numpy.transpose(inputs))
pass
# query the neural network
def query(self, inputs_list):
# convert inputs list to 2d array
inputs = numpy.array(inputs_list, ndmin=2).T
# calculate signals into hidden layer
# 计算隐藏层的输入
# numpy.dot(X,Y)的意思是两个数组的点乘
hidden_inputs = numpy.dot(self.wih, inputs)
# calculate the signals emerging from hidden layer
# 计算隐藏层的输出
hidden_outputs = self.activation_function(hidden_inputs)
# calculate signals into final output layer
# 计算输出层的输入
final_inputs = numpy.dot(self.who, hidden_outputs)
# calculate the signals emerging from final output layer
# 计算输出层的输出
final_outputs = self.activation_function(final_inputs)
return final_outputs
# backquery the neural network
# 反向向后查询函数
def backquery(self, targets_list):
# transpose the targets list to a vertical array
# 获取输出层的输出,这里的输入本来就是标准的0.01到0.99,所以不需要调整
final_outputs = numpy.array(targets_list, ndmin=2).T
# calculate the signal into the final output layer
# 通过反向sigmod函数获取输出层的输入
final_inputs = self.inverse_activation_function(final_outputs)
# calculate the signal out of the hidden layer
# 通过和链接权值计算,得到隐藏层的输出
hidden_outputs = numpy.dot(self.who.T, final_inputs)
# scale them back to 0.01 to 0.99
# 将输出调整到有效的范围,即0.01到0.99,才能用反向sigmod函数,得到sigmod函数的输入
hidden_outputs -= numpy.min(hidden_outputs)
hidden_outputs /= numpy.max(hidden_outputs)
hidden_outputs *= 0.98
hidden_outputs += 0.01
# calculate the signal into the hidden layer
# 通过反向sigmod函数得到隐藏层的输入
hidden_inputs = self.inverse_activation_function(hidden_outputs)
# calculate the signal out of the input layer
# 通过和链接计算,得到输入层的输出
inputs = numpy.dot(self.wih.T, hidden_inputs)
# scale them back to 0.01 to 0.99
# 将输出调整到有效的范围,即0.01到0.99,才是反向sigmod函数,得到sigmod函数的输入
inputs -= numpy.min(inputs)
inputs /= numpy.max(inputs)
inputs *= 0.98
inputs += 0.01
return inputs
# number of input, hidden and output nodes
# 设置输入,隐藏和输出层节点的数量
# 输出层有28*28=784个数据
input_nodes = 784
# 这个自己随便设的
hidden_nodes = 200
# 按本例子的的方案,输出有10中,结点有10个
output_nodes = 10
# learning rate is 0.2
# 设置学习率为0.2
learning_rate = 0.2
# create instance of neural network
# 创建一个神经网络的实例
n = neuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
# run the network backwards, given a label, see what image it produces
for i in range(10):
# label to test
label = i
# create the output signals for this label
targets = numpy.zeros(output_nodes) + 0.01
# all_values[0] is the target label for this record
targets[label] = 0.99
print(targets)
# get image data
image_data = n.backquery(targets)
# plot image data
matplotlib.pyplot.imshow(image_data.reshape(
28, 28), cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
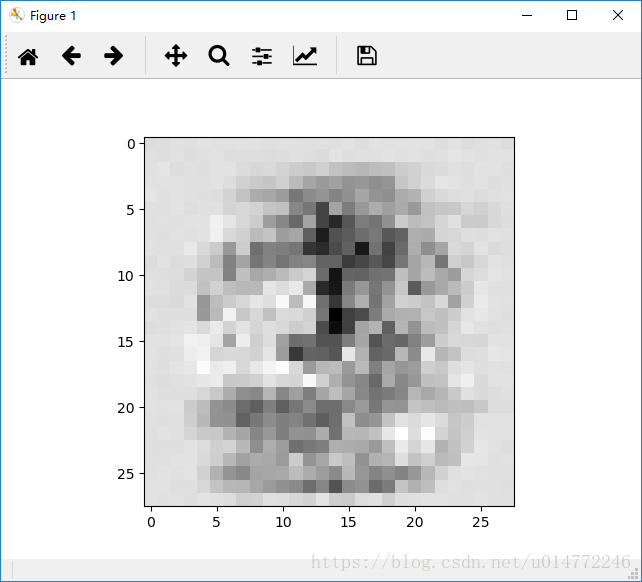
输出从0到9依次为:
0:
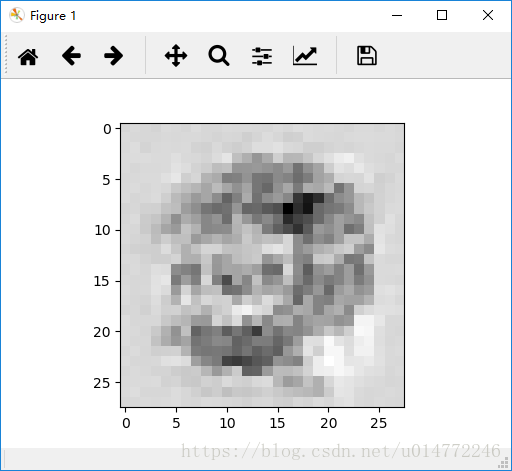
1:
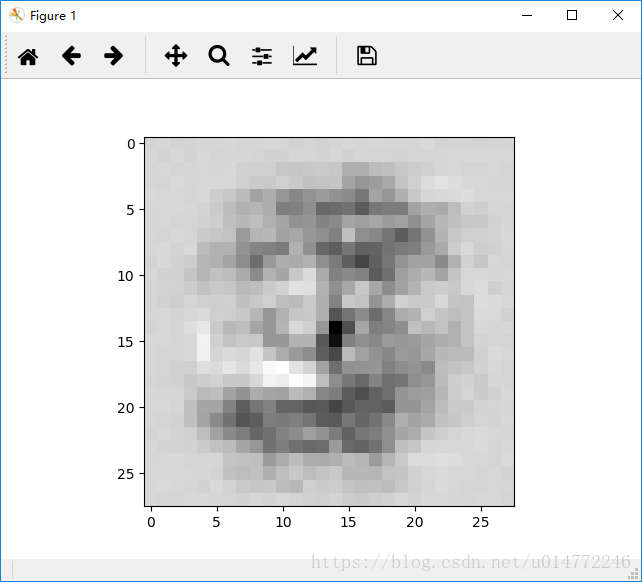
2:
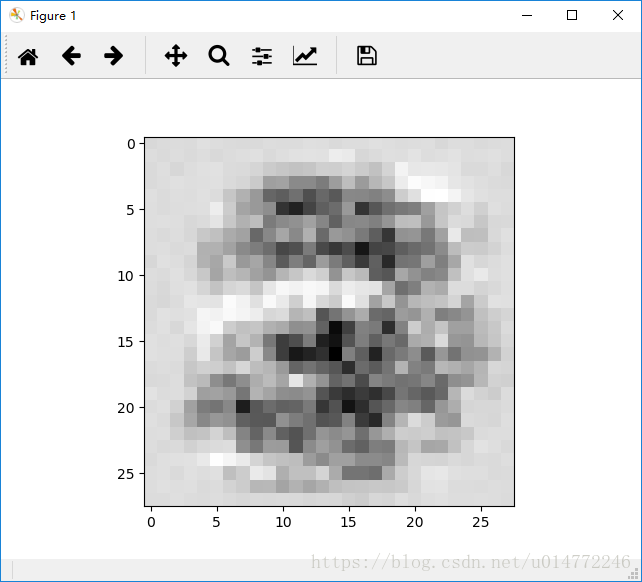
3:
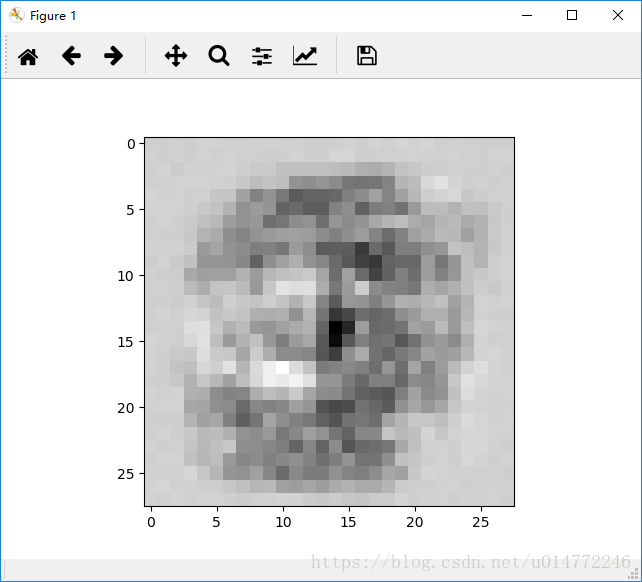
4:
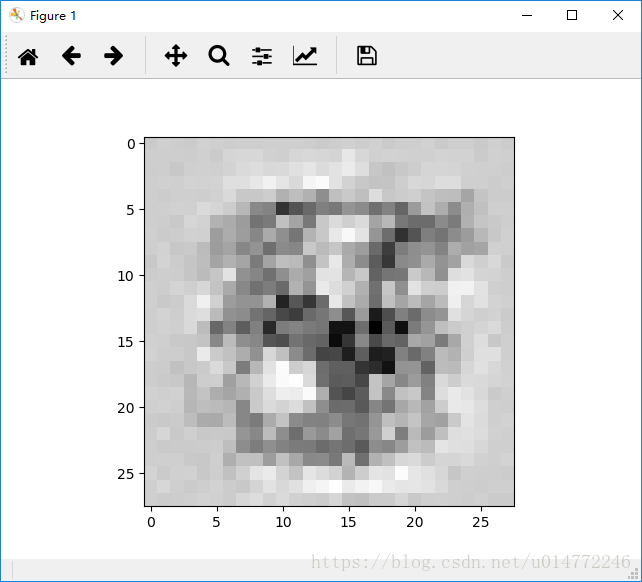
5:
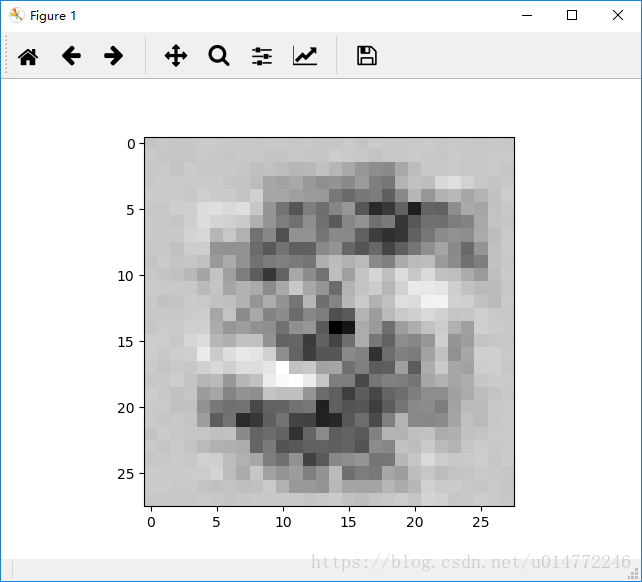
6:
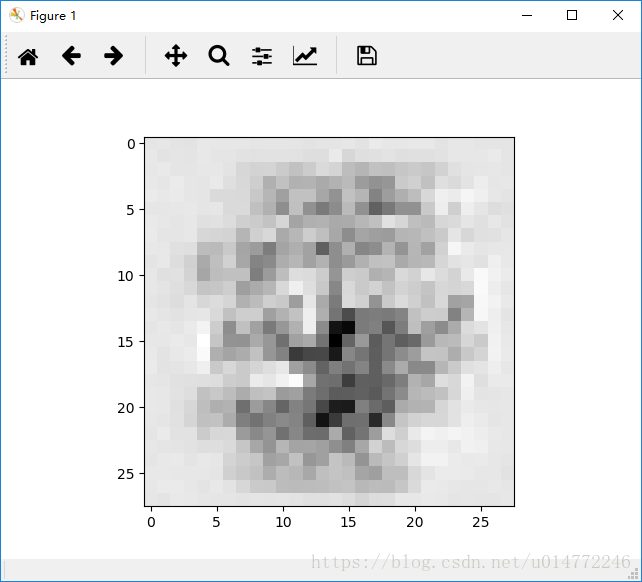
7:
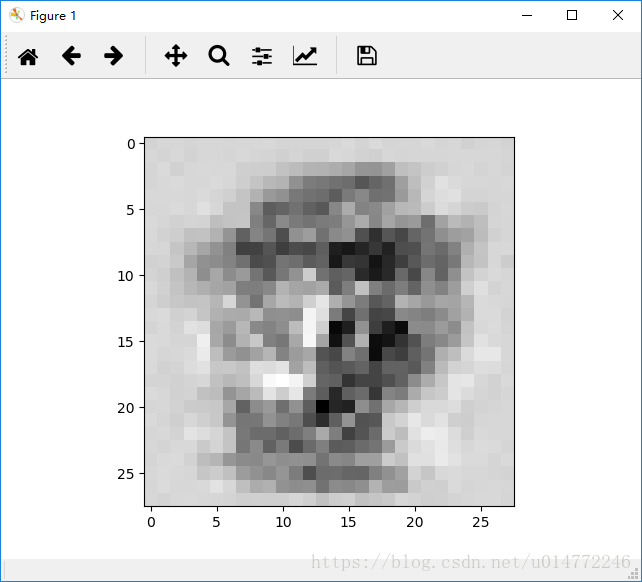
8:
3.3、创建新的训练数据:旋转图像
1、神经网络的训练数据需要有各种各样各种情况的,比如,需要有各种风格的书写。有两个方法丰富数据集,一个是收集尽可能多的数据,另一个是对现有的数据进行压缩,旋转等操作。
对于旋转操作,最好是旋转+10度(也就是逆时针旋转10度)到-10度(也就是顺时针转转10度)的范围内,否则就会造成错误的数据,即实际上不能代表数字的图像,就会导致神经网络的性能下降。
2、作者给出了关于旋转操作的代码:
# 旋转图片作者的代码
import numpy
# 显示图像的操作需要用到这个模块
import matplotlib.pyplot
# scipy.ndimage for rotating image arrays
# 旋转图片的操作需要用到这个模块
import scipy.ndimage
# open the CSV file and read its contents into a list
# 打开测试集的文件,获取数据
data_file = open("mnist_dataset/mnist_test.csv", 'r')
data_list = data_file.readlines()
data_file.close()
# which record will be use
# 选择某条记录
record = 6
# scale input to range 0.01 to 1.00
# 对选定的记录进行处理
all_values = data_list[record].split(',')
scaled_input = (
(numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01).reshape(28, 28)
# plot the original image
# 显示原图像
matplotlib.pyplot.imshow(scaled_input, cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
# create rotated variations
# 创建旋转后的数组
# rotated anticlockwise by 10 degrees
# 逆时针旋转10度后的数组
# 第一个参数为原数据,第二个参数为旋转的度数,顺时针为负,逆时针为证
# 第三个参数为空白区域填充的数值,第四个参数为几次方样条数据差值(不明觉厉),范围是0~5
# 第五个参数为是否改变形状,false是否
inputs_plus10_img = scipy.ndimage.rotate(
scaled_input, 10.0, cval=0.01, order=1, reshape=False)
# rotated clockwise by 10 degrees
# 顺时针旋转10度后的数组
inputs_minus10_img = scipy.ndimage.rotate(
scaled_input, -10.0, cval=0.01, order=1, reshape=False)
# plot the +10 degree rotated variation
# 逆时针旋转10度后的图像
# 第一个参数是要画图的数据,第二个参数是灰度显示,
# 第三个参数是interpolation=None(无差值),
matplotlib.pyplot.imshow(inputs_plus10_img, cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
# plot the +10 degree rotated variation
# 顺时针旋转10度后的图像
matplotlib.pyplot.imshow(
inputs_minus10_img, cmap='Greys', interpolation='None')
matplotlib.pyplot.show()
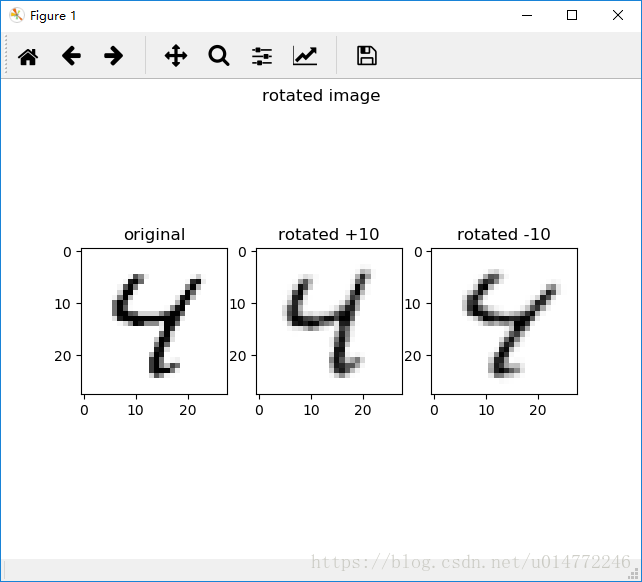
输出的原图像:
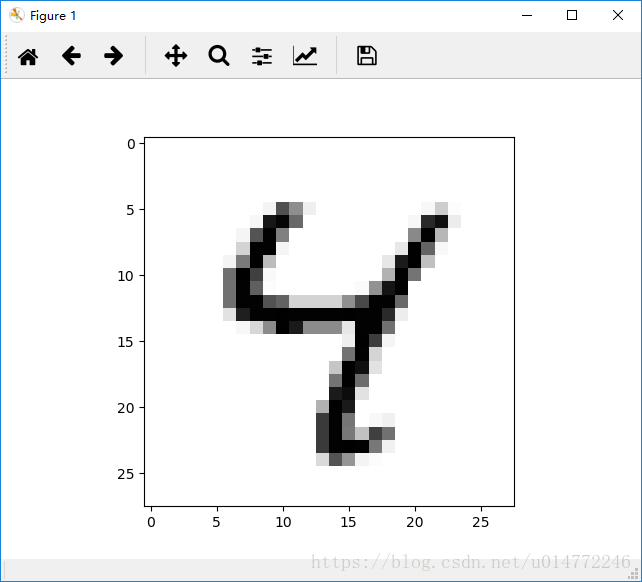
输出的逆时针旋转10度的图像:
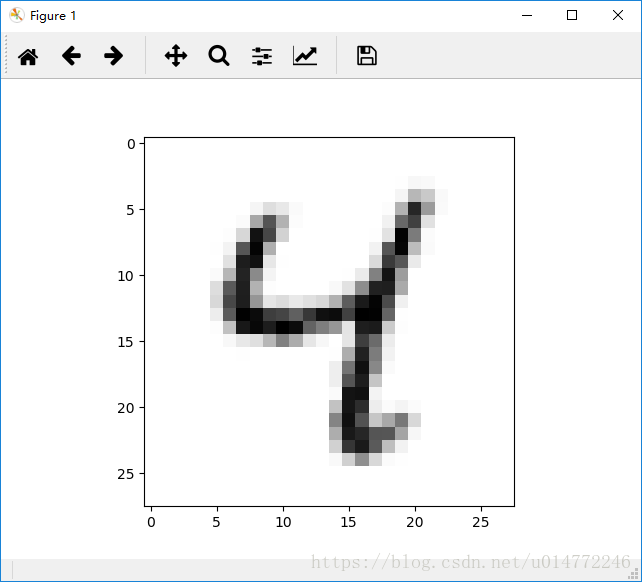
输出的顺时针旋转10度的图像:
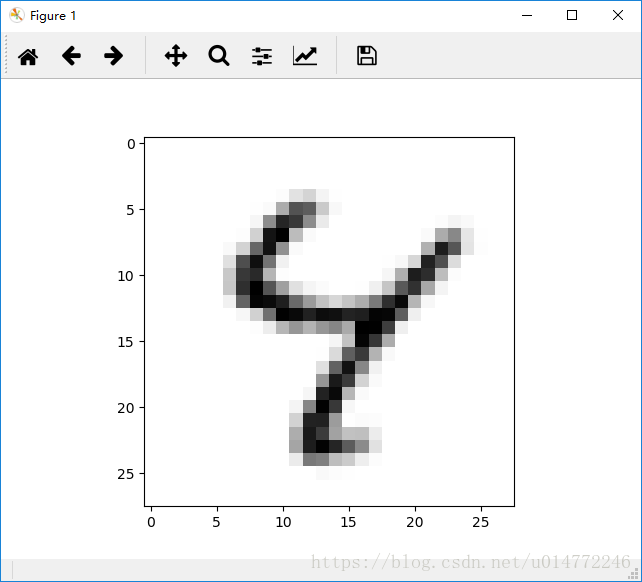
3、我查了下inshow()和show()两个函数的用法,发现一个有趣的使用,所以,改进了原程序,如下:
# 旋转图片作者的代码
import numpy
# 显示图像的操作需要用到这个模块
import matplotlib.pyplot
# scipy.ndimage for rotating image arrays
# 旋转图片的操作需要用到这个模块
import scipy.ndimage
# open the CSV file and read its contents into a list
# 打开测试集的文件,获取数据
data_file = open("mnist_dataset/mnist_test.csv", 'r')
data_list = data_file.readlines()
data_file.close()
# which record will be use
# 选择某条记录
record = 6
# scale input to range 0.01 to 1.00
# 对选定的记录进行处理
all_values = data_list[record].split(',')
scaled_input = (
(numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01).reshape(28, 28)
# create rotated variations
# 创建旋转后的数组
# rotated anticlockwise by 10 degrees
# 逆时针旋转10度后的数组
# 第一个参数为原数据,第二个参数为旋转的度数,顺时针为负,逆时针为证
# 第三个参数为空白区域填充的数值,第四个参数为几次方样条数据差值(不明觉厉),范围是0~5
# 第五个参数为是否改变形状,false是否
inputs_plus10_img = scipy.ndimage.rotate(
scaled_input, 10.0, cval=0.01, order=1, reshape=False)
# rotated clockwise by 10 degrees
# 顺时针旋转10度后的数组
inputs_minus10_img = scipy.ndimage.rotate(
scaled_input, -10.0, cval=0.01, order=1, reshape=False)
# 创建一个空的图像窗口
fig = matplotlib.pyplot.figure()
# 绘制1×3一行三列共3个subplot图像,当前选中第一个。编号从1开始。
# 必须用add_subplot()创建一个或多个子sunplot绘图区才能绘图。
# 第一个子图
# 显示原图像
ax1 = fig.add_subplot(131)
ax1.imshow(scaled_input, cmap='Greys', interpolation='None')
# 设置子图的标题
ax1.set_title('original')
# 第二个子图
# plot the +10 degree rotated variation
# 逆时针旋转10度后的图像
ax2 = fig.add_subplot(132)
# 第一个参数是要画图的数据,第二个参数是灰度显示,
# 第三个参数是interpolation=None(无差值),
ax2.imshow(inputs_plus10_img, cmap='Greys', interpolation='None')
# 设置子图的标题
ax2.set_title('rotated +10')
# 第三个子图
# 顺时针旋转10度后的图像
ax3 = fig.add_subplot(133)
ax3.imshow(inputs_minus10_img, cmap='Greys', interpolation='None')
# 设置子图的标题
ax3.set_title('rotated -10')
# 设置整个图的标题
matplotlib.pyplot.suptitle("rotated image")
# 显示图像
matplotlib.pyplot.show()
3.4、结语
1、作者对读者一些勉励的话。
2、在此回顾我之前写的代码,我发现我的参数被训练的过多了,一次次得测试,权值数组却总是被以一定的步长去训练,极有可能陷入局部最优,也就是说,每次都从随机的权值数组开始训练也是有一定的道理的。
知道了为什么要从新生成的随机的权值数组开始训练,那么,能不能给一个随机的几率,让神经网络的学习率在小几率的情况下变的很大,然后在变回原来的学习率,这样的话,就有一定的几率跳出局部最优。
另外,书上也说了,当训练了一定的代次以后,把学习率变小一些会更好。这个事情其实就是当快到极值点的时候,应该缩小步长来找,要么每次都跨过最优点岂不是很不好,所以,将学习率与误差结合起来,随着误差的减小,学习率随着减小,这样的话,岂不是就让神经网络更智能化?
思想是这,但是代码还没编,有时间的话,实现以下吧~~~
另:一些说明
1、本博客仅用于学习交流,欢迎大家瞧瞧看看,为了方便大家学习。
2、如果原作者认为侵权,请及时联系我,我的qq是244509154,邮箱是[email protected],我会及时删除侵权文章。
3、我的文章大家如果觉得对您有帮助或者您喜欢,请您在转载的时候请注明来源,不管是我的还是其他原作者,我希望这些有用的文章的作者能被大家记住。
4、最后希望大家多多的交流,提高自己,从而对社会和自己创造更大的价值。