牛客网暑期ACM多校训练营（第六场） C.Generation I (思维+逆元+组合数学)

题目链接

时间限制：C/C++ 3秒，其他语言6秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

Oak is given N empty and non-repeatable sets which are numbered from 1 to N.

Now Oak is going to do N operations. In the i-th operation, he will insert an integer x between 1 and M to every set indexed between i and N.

Oak wonders how many different results he can make after the N operations. Two results are different if and only if there exists a set in one result different from the set with the same index in another result.

Please help Oak calculate the answer. As the answer can be extremely large, output it modulo 998244353.

输入描述:

The input starts with one line containing exactly one integer T which is the number of test cases. (1 ≤ T ≤ 20)

Each test case contains one line with two integers N and M indicating the number of sets and the range of integers. (1 ≤ N ≤ 1018, 1 ≤ M ≤ 1018, )

输出描述:

For each test case, output "Case #x: y" in one line (without quotes), where x is the test case number (starting from 1) and y is the number of different results modulo 998244353.

 

示例1

输入

2
2 2
3 4

输出

Case #1: 4
Case #2: 52

 

题意:T组测试样例,每组样例给出N和M,表示有N个集合(初始为空,且集合元素不重复),M种不同的元素,最后N次操作,第i次可以选择一种编号(1~M)的元素,然后在第i~N个集合中都放一个该元素,问你一共可以产生多少种不同结果?

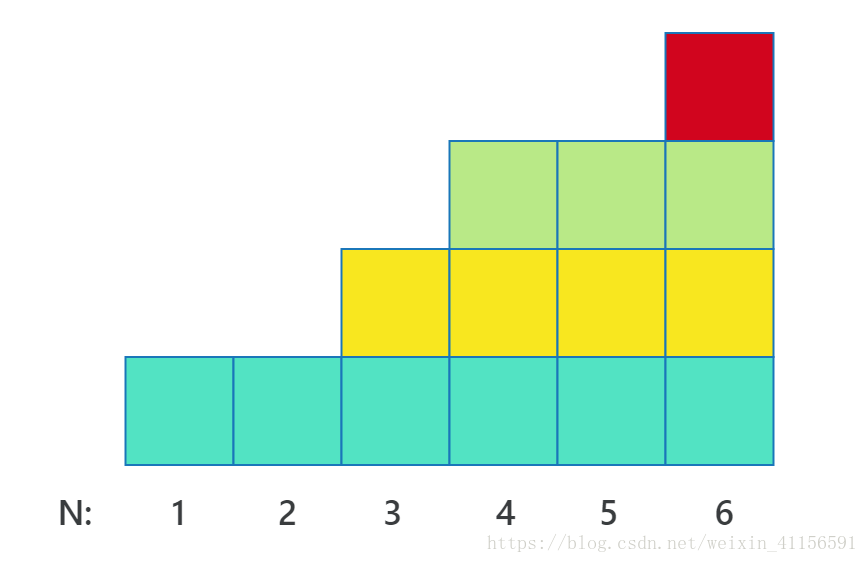
题解:换个思考方式(大佬教的):把1~N当做楼梯,对于每次操作,若是取一种前面都没有取过的颜色(之后都改用颜色,方便看图理解),那么该格楼梯比上一格高一阶,若是取之前去过的任意一种颜色,那么该格楼梯和上一格高度一样如下图:

                        

     上图就和题目的说明一样,应该很容易理解了吧,对于每层的上升就是选择了一种前面没有选择过的颜色,若是选择的是前面选过的任意一种颜色,该处的层数不会上升,而是平的~

      那么下面来计算一下结果:对于给出N个格子,M种颜色,构造这个楼梯最多只能选择min(N,M)种颜色,那么假设当前选择了K种颜色(由于最少选择一种颜色,因此K的范围是1~min(N,M)),那么有种颜色可以选择,且对于这些颜色的上色顺序可以是随意的,那么就有种结果,还有就是对于我们在1~N中选择新颜色投放位置(即阶梯的上升部分),由于第一层一定要放一种颜色,所以剩下K-1种颜色,和N-1个可以选择的投放位置,那么有种结果,乘起来就得到了选K种颜色的情况数:.

      所以可以得到总的情况数为:      K的范围是(1~min(N,M));

      剩下的一点逆元的操作了,我是先对上式子进行化简后求的,且注意预处理出1e6内的逆元表(貌似不弄会TLE的)~

代码如下:

#include
#include
#include
#include
#include
#include
#include
#include