统计学中常见的分布汇总及相关概念
常见分布
统计学中有很多常见的分布,在此对这些分布进行梳理。
离散型随机变量分布
1.离散型均匀分布
若随机变量有n个不同值,具有相同概率,则我们称之为离散均匀分布,通常发生在我们不确定各种情况发生的机会,且认为每个机会都相等,例如:投掷骰子等.
离散型均匀分布
离散型均匀分布-维基百科

2.两点分布/伯努利分布
伯努利分布是二项分布在n=1时的特例。一次随机试验,成功概率为p,失败概率为q=1-p。
伯努利分布
3.二项分布
二项分布是n重伯努利试验成功次数的离散概率分布。
二项分布的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。
二项分布

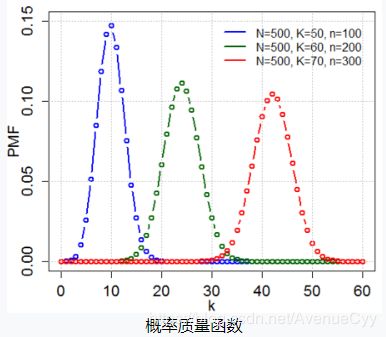
4.超几何分布
对N件产品(其中M件次品)进行不放回抽样,在n次抽样中抽到次品数X,服从超几何分布。
超几何分布
5.几何分布
对N件产品(其中M件次品)进行不放回抽样,在n次抽样中抽到次品数X,X记首次成功的概率,服从几何分布。
几何分布

6.泊松分布
有些事件,我们可以预估这些事件的总数,但是没法知道具体的发生时间。
如,已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?

泊松分布
连续型随机变量分布
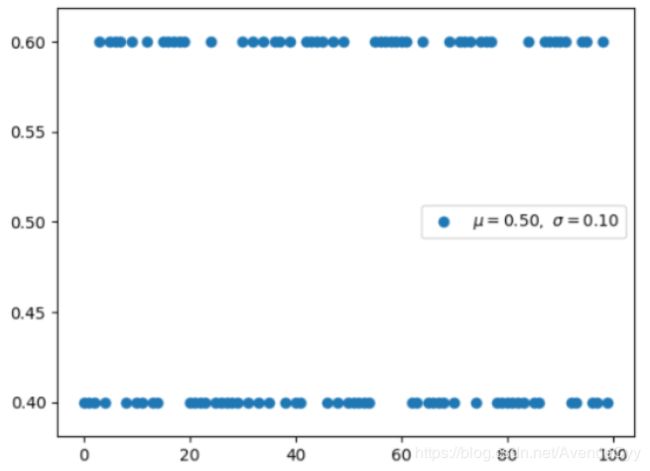
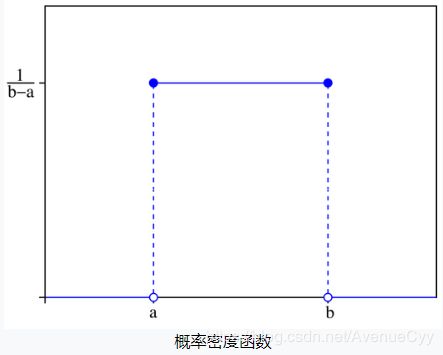
1.连续型均匀分布
均匀分布是指闭区间 [a, b] 内的随机变量,且每一个变量出现的概率是相同的。
连续型均匀分布
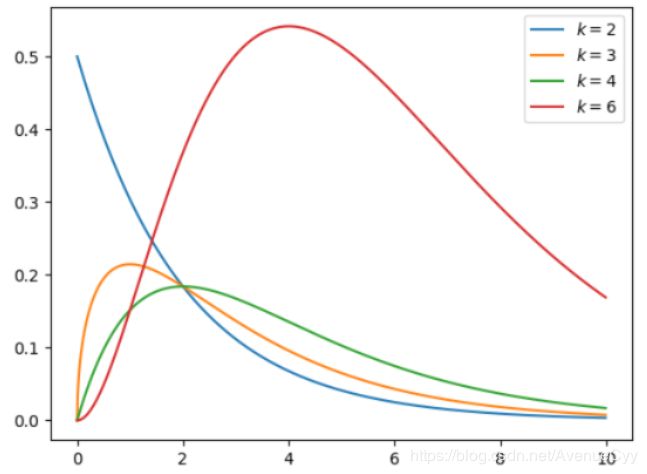
2.指数分布
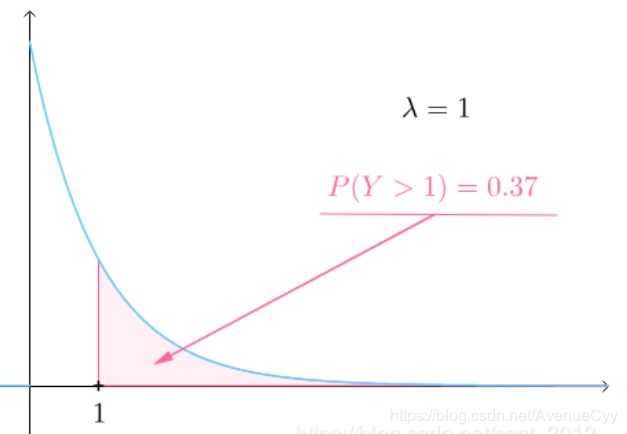
指数分布是事件的时间间隔的概率。
如,婴儿出生的时间间隔。
指数分布
3.正态分布
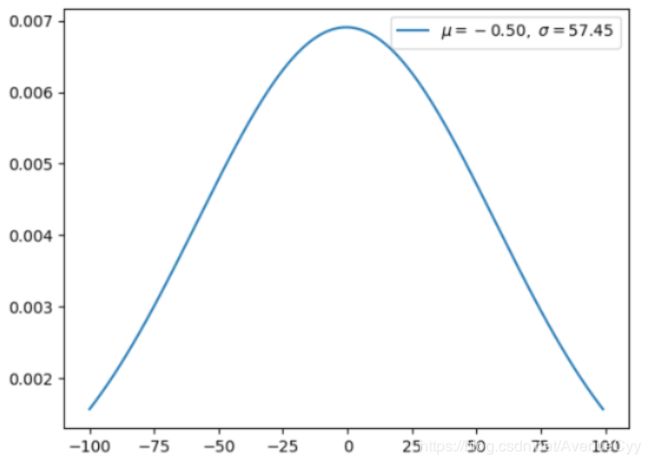
反应误差的最重要的分布,确定了均值和标准差就能确定一种正态分布。
当正态分布的均值为 0、方差为 1 的时候,它就是标准正态分布,这也是我们最常用的分布。
正态分布
4.t分布
t-分布(Student t-distribution)用于根据小样本来估计呈正态分布且变异数未知的总体,其平均值是多少。
t 分布的长尾占比更多,这意味着 t 分布更容易产生远离均值的样本。
学生t-分布

5.卡方分布
卡方分布(Chi-squared)可以理解为,k 个独立的标准正态分布变量的平方和服从自由度为 k 的卡方分布。
卡方分布
6.F分布
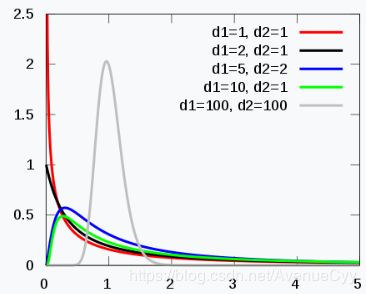
F分布是由2个卡方分布构造的,而卡方分布一般用于度量样本方差和误差之和。所以引出F分布的三个重要应用:两个正态总体的抽样分布、方差分析、回归分析。
数据统计基础之F分布及其应用
F分布及其分布
数字特征
1.期望
相当于平均值。
2.方差
就是方差。
3.协方差
定义表示X, Y 相互关系的数字特征,即协方差。
cov(X, Y) = E(X-E(X))(Y-E(Y))。
当 cov(X, Y)>0时,表明 X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
4.相关系数
相关系数也可以看成协方差:剔除了两个变量量纲影响、标准化后的特殊协方差。
5.数据的概括性度量
1.集中趋势的度量
中位数,均值,众数
2.离散程度的度量
- 分类数据:异众比率
- 顺序数据:四分位差
- 数值型数据:方差和标准差
1.极差
2.平均差
3.方差和标准差
4.相对位置的度量- 标准分数
- 经验法则
- 切比雪夫不等式
- 相对离散程度:离散系数
3.偏态与峰态的度量
偏态系数
峰态系数
大数定律
大数定律:如果实验次数足够大,样本均值就会趋近于总体的期望。
比如,我们投骰子,如果我们投100次,求出现的数的平均,我们觉得会差不多是(1+6)/2=3.5 因为我们按照期望计算,算出来就是3.5。
大数定律
中心极限定理
当满足某些条件的时候,比如样本量比较大,采样次数区域无穷大的时候,样本均值就越接近正态分布。
中心极限定理
文章参考
https://baijiahao.baidu.com/s?id=1645256431232755893&wfr=spider&for=pc
https://www.cnblogs.com/leezx/p/7340045.html