2020 Multi-University Training Contest 3 - 1008. Triangle Collision(计算几何+二分)

题目链接：Triangle Collision

题意：在一个边长为L的等边三角形内有一颗小球，给出初始位置$(x,y)$和速度$(v_x,v_y)$，每次与三角形的三边碰撞都为弹性碰撞，求第k次与边碰撞是在什么时候

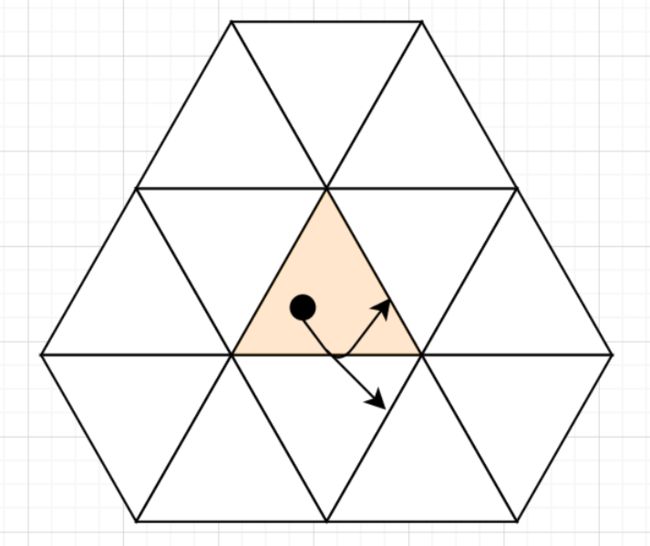
思路：我们可以将三角形进行扩展，如下图所示

可以看做小球在走直线，我们二分时间t，比较小球经过三边的次数与k的大小即可

以求经过三角形的底边为例，在t时间内，小球在y轴上运动的$v_y * t$，那么在t时刻，小球的坐标为$y+v_y * t$

如果$v_y >= 0$，即小球向上走，那么经过三角形底边的次数为$\left \lfloor \frac{y+v_y*t}{H} \right \rfloor$，H为三角形的高

如果$v_y<0$，即小球向下走，那么经过三角形底边的次数为$1-\left \lceil \frac{y+v_y*t}{H} \right \rceil$，注意此时$y+v_y*t$可能为负数，所以应该向上取整

对于另外的两种边，将坐标和速度都翻转一下，公式如下：

$y'=\frac{\left | H-\sqrt3 x-y \right |}{2}$，$v_y'=-\frac{\sqrt3}{2}v_x-\frac{1}{2}v_y$

$y''=\frac{\left | H+\sqrt3 x-y \right |}{2}$，$v_y''=\frac{\sqrt3}{2}v_x-\frac{1}{2}v_y$

图片参考：https://blog.csdn.net/qq_43680965/article/details/107647739

#include 
#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const double sq3 = sqrt(3);
const double eps = 1e-6;

int T;
ll k;
double L, x, y, vx, vy;

ll solve(double y, double vy, double t)
{
    double H = sq3 * L / 2, x = (y + vy * t) / H;
    if (vy >= 0) return abs(floor(x));
    return abs(1 - ceil(x));
}

int main()
{
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    scanf("%d", &T);
    while (T--) {
        scanf("%lf%lf%lf%lf%lf%lld", &L, &x, &y, &vx, &vy, &k);
        double H = sq3 * L / 2, l = 0, r = 100000000000;
        while (r - l > eps) {
            double mid = (l + r) / 2;
            ll a = solve(y, vy, mid);
            ll b = solve(abs(H - sq3 * x - y) / 2, -vy / 2 - sq3 * vx / 2, mid);
            ll c = solve(abs(H + sq3 * x - y) / 2, sq3 * vx / 2 - vy / 2, mid);
            if (a + b + c >= k) r = mid;
            else l = mid;
        }
        printf("%.8lf\n", l);
    }
    return 0;
}