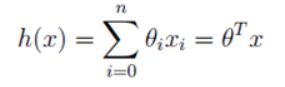Andrew Ng Machine learning——Work(One)——Linear regression——Univerate(Based on Python 3.7)
Python 3.7
所用数据链接::https://pan.baidu.com/s/1YGsencu8wrilvrjuSteGZQ
提取码:c3yy
目录
- Univerate linear regression
- 1.0 package
- 1.1 load data
- 1.2 visualization data
- 1.3 data preprocessing
- 1.4 define costfunction
- 1.5 gradientdescend
- 1.6 visualization result
Univerate linear regression
题目:为选定创办超市地点,我们有来自多个不同城市的人口(x)和利润(y) 数据,先希望根据这些数据利用线性回归来预测利润与人口的关系,从而选择超市创办地点。
1.0 package
首先引入相应的包,以便后续使用。
import numpy as np #处理矩阵,转换数据格式必备
import pandas as pd #读取数据,加工数据
import matplotlib.pyplot as plt #绘图
1.1 load data
读入数据,代码如下:
def load_data(path): #定义函数,名为load_data,有一个参数path
data=pd.read_csv(path,header=None,names=['population','profit'])
#读取数据,其中path为数据路径,header代表列索引,默认为0,也就是以第一行为列索引,这里关闭默认,改用后面的names为列索引
return data ,data.head(),data.describe()
# 返回数据,表头以及数据的统计信息
查看返回值:
data,data_head,data_describe=load_data('ex1data1.txt')
print(data_head)
print(data_describe)
1.2 visualization data
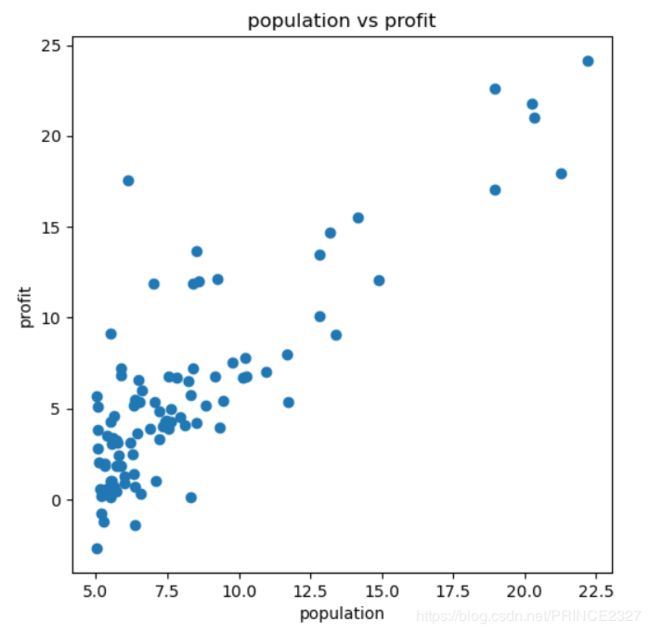
读取完数据后,最好能够将其可视化,以加深对数据的直观认识。事实上这一步虽然不是算法的核心,但个人认为对于数据分布的直观认识往往也十分重要,下面给出代码:
def visualization_data():
#定义函数,函数名称为cisualization_data,无传入变量
fig,ax=plt.subplots(figsize=(6,6))
# fig可以理解为创建一个画布,ax可以理解为画布中的具体内容,figsize指明画布大小为6*6
ax.scatter(data['population'],data['profit'])
#scatter指明画图类型为散点图,其中传入参数,前两个为位置参数,按位置对应依次为散点的x坐标和y坐标,第三个参数label指明了该图的名称
ax.set_xlabel('population')
#设置横坐标名称为 population
ax.set_ylabel('profit')
# 设置纵坐标名称为 profit
ax.set_title('population vs profit')
# 设置该图主题为 population vs profit
plt.show()
# 可视化
1.3 data preprocessing
所谓数据预处理似乎也谈不上,只是按照要求改变以下数据罢了,代码如下:
def data_preprocessing():
# 定义函数,名为data_processing,无传入参数
data.insert(0,'one',1)
#将之前的data,在第0列(也就是我们认知的第一列)加一列1,并将索引设置为one
#这一步是为了后续的向量化
col=data.shape[1]
# 返回data的列数(如果方括号里是0返回的则是行数)
x=data.iloc[:,:col-1]
#类似切片,选取data中第1到第col-1列的所有行作为x
y=data.iloc[:,col-1:]
# 选取data中最后一列所有行作为y
return x,y
# 返回x,y
x,y=data_preprocessing()
#print(x)
#print(y)
x=np.array(x.values)
y=np.array(y.values)
#将x,y转换为数组形式
1.4 define costfunction
def costfunction(x,y,theta):
# 定义函数,名为costfunction,传入三个参数:x,y,theta
h=x@theta.T
# 计算h_{theta}(x)
temp=np.power((h-y),2)
# 实际上这并没有什么用,只是将计算分解,降低出错。
# power 中第一个参数,表示求次方的对象,第二个参数,表示求的次方数
J=np.sum(temp-h)/(2*len(x))
# 计算式
return J
# 返回J
J=costfunction(x,y,theta)
print(J)
# 观察初始代价 32.0727......
好了,接下来就是梯度下降了
1.5 gradientdescend
def gradientdescend(x,y,theta,alpha,num_iter):
# 定义函数,名为gradientdescend ,传入参数x,y,theta,alpha,num_iter
theta_t=np.array(np.zeros(theta.shape))
# 初始化theta
cost=np.zeros(num_iter)
# 生成一个长度为迭代次数的数组,后续记录每一次迭代后的代价函数值
m=len(x)
for i in range(num_iter):
# 每次迭代均执行如下操作
theta_t=theta-(alpha/m)*(x@theta.T-y).T@x
# 梯度下降
theta=theta_t
# 将更新后的theta赋值
cost[i]=costfunction(x,y,theta)
# 记录每一次代价函数值
return theta,cost
# 返回
alpha=0.01
#指明学习率
iterations=1000
#指明迭代次数
fin_theta,cost=gradientdescend(x,y,theta,alpha,iterations)
fin_cost=costfunction(x,y,fin_theta)
print('fin_cost',fin_cost)
# 查看最终的代价函数值(迭代1000此后),大约为4.51595
1.6 visualization result
核心工作已做完,接下来就是可视化结果,代码如下:
x=np.linspace(data.population.min(),data.population.max(),200)
# 就是在data中从population列中最小的值到最大的值这个区间中,选取200个点
f=fin_theta[0,0]+(fin_theta[0,1]*x)
# 计算相应的纵坐标
fig,ax=plt.subplots(figsize=(8,8))
# 创建一个画布,尺寸为8*8
ax.plot(x,f,'black',label='predition')
# 指明要画的对象横坐标为x,纵坐标为f,颜色为黑色(个人喜好黑色,总感觉看起来很高雅
ax.scatter(data['population'],data['profit'])
# 指明现在要画散点图,并且横坐标为data中的population列,纵坐标为data中的profit列
ax.set_xlabel('population')
# 设置横坐标名称
ax.set_ylabel('profit')
# 设置纵坐标名称
ax.set_title('population vs profit')
# 设置图主题
plt.show()
#显示
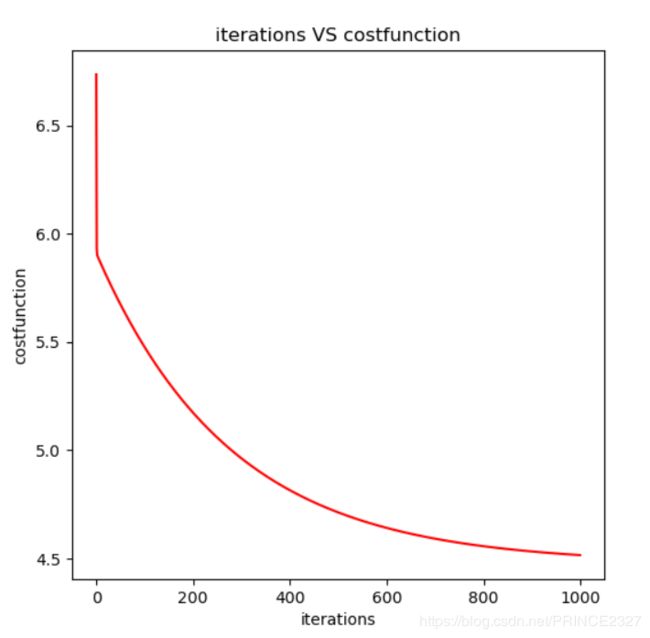
fig,ax=plt.subplots(figsize=(6,6))
ax.plot(np.arange(iterations),cost,'r')
ax.set_xlabel('iterations')
ax.set_ylabel('costfunction')
ax.set_title('iterations VS costfunction')
plt.show()
#代码解释同上
结果如下:
至此,已经实现了对于单特征的线性回归。建议读者在读懂代码后,自己动手写,以便加深理解。
未经允许,请勿转载。
欢迎交流。