Andrew Ng Machine learning——Work(One)——Logistic regression——Bipartition(Based on Python 3.7)

                    Python 3.7

所用数据链接：二元逻辑回归数据(ex2data2.txt),提取码：c3yy

Bipartition Logistic regression

题目：为根据两门考试预测某一学生能否被录取，我们收集了多组数据，其中每一个数据样本包括三个信息（考试一成绩，考试二成绩，被录取情况），希望通过这些数据训练出一个二元逻辑回归器，从而进行预测。

1.0 Package

老规矩，先进包：

import numpy as np
# 数据处理（尤其是矩阵，数组等）
import pandas as pd
# 数据格式转换及加工
import matplotlib.pyplot as plt
# 画图必备
import scipy.optimize as opt
# 高级优化函数（不用这个自己写梯度下降也可以）

1.1 Load data

第一步永远是读取数据，代码如下：

def load_data(path):
# 定义函数，传入参数path
    data=pd.read_csv(path,names=['test1','test2','accept'])
# 读取path指向的文件，读出来为Dataframe型，并将列索引依次改为names中的三个
    return data,data.head(),data.describe()
# data.head()为头文件，即简略反映该文件，data.describe()为data中数据的统计信息
data,data_head,data_describe=load_data('ex2data1.txt')
# 调用函数
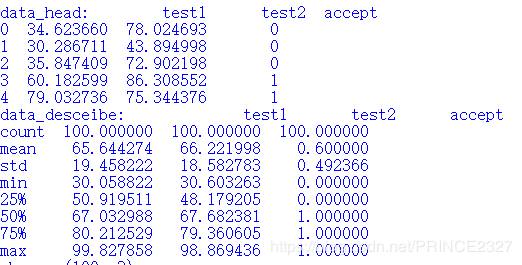
print('data_head:',data_head)
print('data_desceibe:',data_describe)

输入如下：

1.2 Visualization data

成功读取后，尽量可视化数据，有助于对于数据的直观理解，代码如下：

def view_data():
#定义函数，不传入参数
    pos_data=data[data.accept.isin(['1'])]
# data.accept.isin（[]）指返回data中accept列值为1的行索引，从而返回正样本点，返回类型为Dataframe
    neg_data=data[data.accept.isin(['0'])]
# 同上，返回负样本点
    fig,ax=plt.subplots(figsize=(6,6))
# 创建画布及对象，画布尺寸为6*6   
    ax.scatter(pos_data['test1'],pos_data['test2'],label='Accepted')
# 画正样本点 
    ax.scatter(neg_data['test1'],neg_data['test2'],label='Rejected')
# 画负样本点
    ax.legend()
# 显示标签
    ax.set_xlabel('Score of test1')
# 设置横轴名称
    ax.set_ylabel('Score of test2')
# 设置纵轴名称
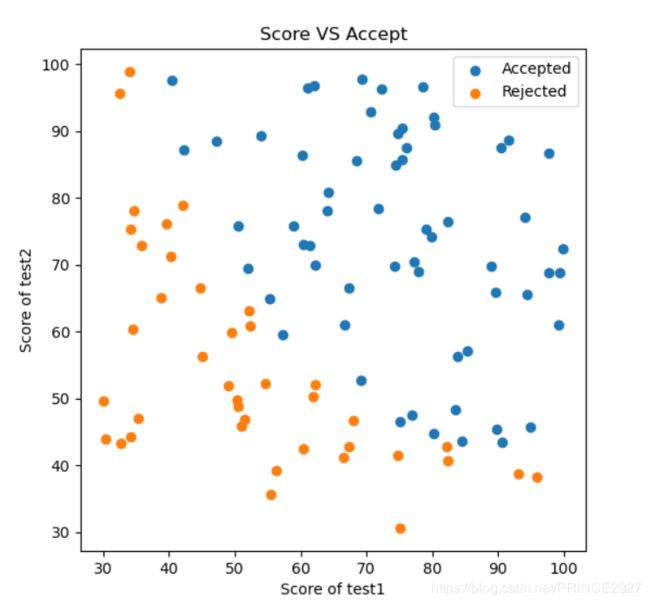
    ax.set_title('Score VS Accept')
# 设置图主题
    plt.show()
# 可视化
view_data()
# 调用函数

输出如下：

很漂亮，下面进入数据预处理。

1.3 Data processing

def sigmoid(z):
# 定义sigmoid函数
    return 1/(1+np.exp(-z))
def preprocess_data(data):
# 定义数据预处理函数，传入参数data
    data.insert(0,'one',1)
# 第一列加一列1，方便后续向量化
    x=(data.iloc[:,:-1]).values
# 取data中除倒数第一列的所有列的所有行，并将其转换为数组形式，作为x
    y=(data.iloc[:,-1]).values
# 同上
    return x,y
# 返回
x,y=preprocess_data(data)
# 调用
print('shape_x{}'.format(x.shape))
# 输出形状 （100，3）
print('shape_y{}'.format(y.shape))
# （100，）
theta=np.zeros(x.shape[1])
# （3，）

准备工作做好后，下面逐渐进入算法的核心

1.4 Costfunction

二元逻辑回归的代价函数见下图：

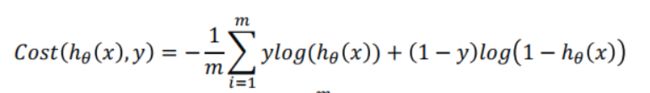
其中：

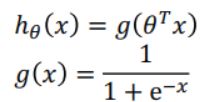
之所以这样定义代价函数而舍弃平方误差形式，是为了保证代价函数是凸函数，从而保证梯度下降能够收敛到全局最小值。下面给出代码：

def costfunction(theta,x,y):
# 定义代价函数，传入参数
    h=x@theta
    cost=sum((-y)*np.log(sigmoid(h))-(1-y)*np.log(1-sigmoid(h)))/(len(x))
# 计算损失函数值
    return cost
# 返回
cost=costfunction(theta,x,y)
print('initial_cost:',cost)
# 查看初始损失值 0.69134......

1.5 Gradientdescent

下面定义梯度：

def gradientdescent(theta,x,y):
# 定义函数
    h=x@theta
    gradient=(x.T@(sigmoid(h)-y))/(len(x))
# 计算梯度值
    return gradient
gradient=gradientdescent(theta,x,y)
print('initial_gradient:',gradient)
# 查看初始梯度值  [ -0.1        -12.00921659 -11.26284221]

1.6 Training model

下面，我们引入高级优化算法，并传入自定义的代价函数和梯度函数，计算最优解：

def training():
# 定义函数
    result=opt.minimize(fun=costfunction,x0=theta,args=(x,y),method='TNC',jac=gradientdescent)
# 调用minimize函数
    return result['x']
# 返回结果中索引为x的值（也即最优解）
fin_theta=training()
# 查看最优theta
#print(fin_theta)
# [-25.1613186    0.20623159   0.20147149]

1.7 Plot Decision Boundary

完成了模型训练后，我们希望可视化结果，以便直观地了解分类效果，代码如下：

def plot_boundary(theta,x):
# 定义函数
    x1=np.linspace(20,100,200)
# 指定x1范围，从（20，100）中选取200个点
    x2=-(theta[0]+x1*theta[1])/theta[2]
# 根据公式可推导出x2与x1关系从而计算出x2值
    fig,ax=plt.subplots(figsize=(6,6))
    pos_data=data[data.accept.isin(['1'])]
    neg_data=data[data.accept.isin(['0'])]
# 意义同数据可视化中代码
   ax.scatter(pos_data['test1'],pos_data['test2'],label='Accepted')
    ax.scatter(neg_data['test1'],neg_data['test2'],label='Rejected')
# 分别画出正负样本
    ax.plot(x1,x2)
# 画出x1,x2的函数关系图
    ax.set_xlabel('Test1')
    ax.set_ylabel('Test2')
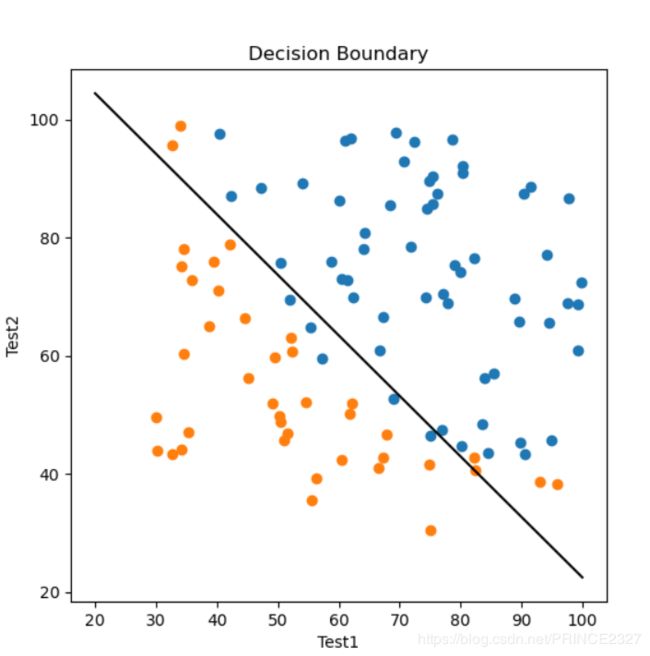
    ax.set_title('Decision Boundary')
# 设置标签
    plt.show()
# 可视化
plot_boundary(fin_theta,x)

输出如下：

结果还是相当美好，下面对该模型进行评估。

1.8 Evalute model

评估代码如下：

def model_predict(theta,x):
# 定义函数
    predict=sigmoid(x@theta)
# 输出训练模型判断值
    return [1 if i>=0.5 else 0 for i in predict]
# 根据predict的值与0.5的大小返回0或1，列表形式
result=model_predict(fin_theta,x)
print(result)
# 返回预测列表
def model_evaluation(theta,x):
# 定义函数
    accuracy=sum([1 if i==j else 0 for (i,j) in zip(result,y)])/len(x)
# zip意为打包为数组，当reslut中的某一个值（预测标签）和y(真实标签）相同时，返回1，否则0
    return accuracy
accuracy=model_evaluation(fin_theta,x)
#print('The accuracy of the model is{}{}'.format(accuracy*100,'%'))
# 输出准确率 89%

1.9 Apply module

训练一个模型最终目的是为了应用，我们已经看到，模型的训练效果还算不错(虽然这种检验方法是有问题），所以我们打算将其投入使用以预测某一个学生是否能够被录取：

def predict(fin_theta,a,b):
# 定义函数
    h=fin_theta[0]+fin_theta[1]*a+fin_theta[2]*b
    h=sigmoid(h)
# 计算激活值
    if h >0.5:
        print("You might be admitted,but I'm not sure,Good luck")
    else:
        print("You might be rejected,but I'm not sure,Good luck") # 根据激活值与0.5大小输出预测结果
a=float(input('Please tell me your score of test1:'))
b=float(input('Please tell me your score of test2:'))
predict(fin_theta,a,b)
# 调用

输出如下：

至此，已经完成了二元逻辑回归。希望读者吃透代码后反复练习以加深印象。

未经允许，请勿转载。

欢迎交流