2018研究生数学建模竞赛B题-光传送网建模与价值评估-竞赛总结
---恢复内容开始---
2018研究生数学建模竞赛B题-光传送网建模与价值评估-竞赛总结
这道赛题是有关通信方面的赛题,初步读题,感到第一问和第二问关系不大,第二问和第三问关系也不大,不过第一问和第三问有比较紧密的顺承关系.
1-1
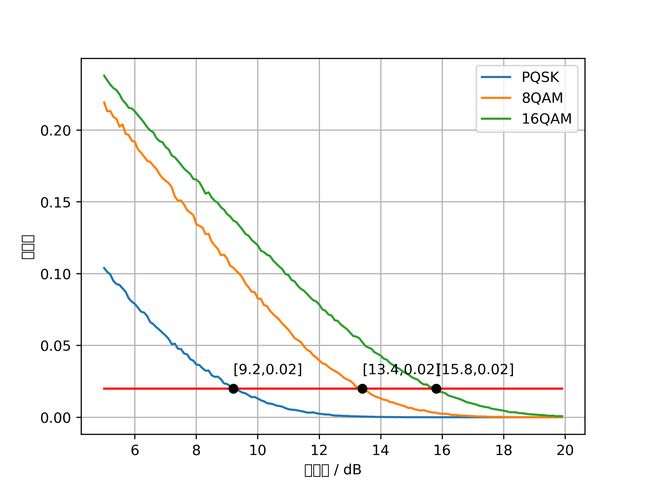
第一问主要讨论在光纤通信环境下,与光信号传输有关的调制解调的误码率问题.在题设条件中,纠前误码率(BER)只与信噪比(SNR)有关.因此题目要求我们建立数学模型描述两者的关系.
对于该问题有两种思路:
- 建立机理模型
也就是通过对光纤中的入纤信号,与信号噪声进行概率描述,然后推导出出纤信号的概率描述,从而通过对概率密度函数的二重积分,直接计算出两者的解析关系.
- 实验模型
也就是使用计算机仿真的方式,通过大量的实验,模拟信号输入,编码,噪声输入,解码,计算误码率的过程,对误码率进行计算.根据大数定律,大量实验的结果会趋近于第一种思路的机理模型的解.
- 两种方法的比较
第一种方法有着更强的数学要求,但是推到的结果显示,最后的结果是一个正态分布函数的二重积分的加权和.计算这个函数的积分其实十分困难,还是要借助数值计算的工具或者查表.无法有效的得到一条表达式.
第二种方法较容易实现,但是在试验次数较小的情况下,得到的曲线会引入较大误差.造成求解曲线的不平滑.因此得到平滑的曲线需要花费较大的计算时间.在我的电脑上计算时间大概有半个小时.
在这里给出一张求解图.
1-2
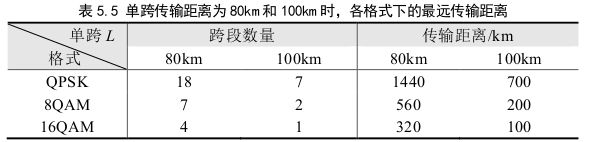
第二问主要是对整个传输的光路进行建模,要考虑光在线缆中引入的噪声,光放大器引入的噪声,光在线缆中的功率衰减等因素,结合上文中算出的一个参数求解传输链路的段数.
在这里给出模型和结果.
结果
2-1
第二问似乎与第一问没有必然的联系,这是一个整数规划的问题,特别是在第一问中,这个证书规划非常的纯粹,因此可以直接建立整数规划的模型,使用相应的求解器进行求解.
我们将问题直接转化成了MIP问题,然后使用GUROBI工具进行求解.
转化成的问题如下图.
其中Cij 表示 i 节点与 j 节点之间的传输容量,可依据节点间的距离选择相应的传输格式,从而判断传输容量的大小。本文认为,若要使网络价值最大化,必须要以容量利用率最大为标准来分配传输格式。
λ ij 表示 i 节点与 j 节点之间链路的权重,M 为光传输网络的节点数。
H i ,H j 分别表示 i 节点和 j 节点的人口数。当所有节点的链接情况由决策
信息R ij 确定时,目标函数值中相应的未知变量可进一步求出并确定目标函数值.
约束中限制了网络连接数,和孤立链路数量.
值得一题的是孤立链路这个约束.
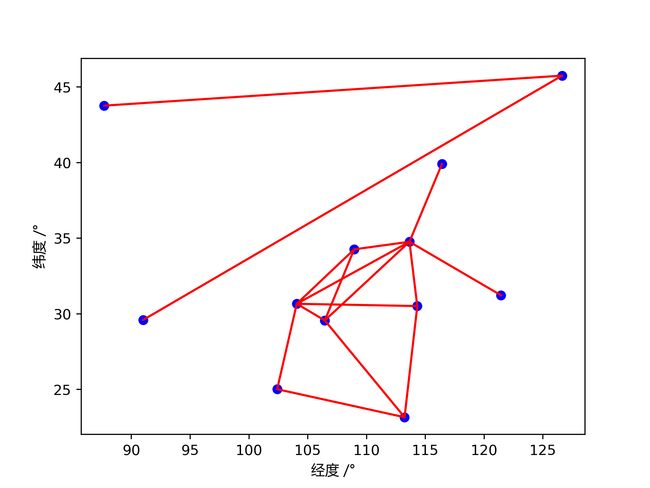
在一开始我们解出的解如下图:
可以看到,得到的解并不是一个连通的图.但是作为一个光纤网络来说,必然要求我们解出一个连通图.因此我们加入了孤立链路这个新的约束.
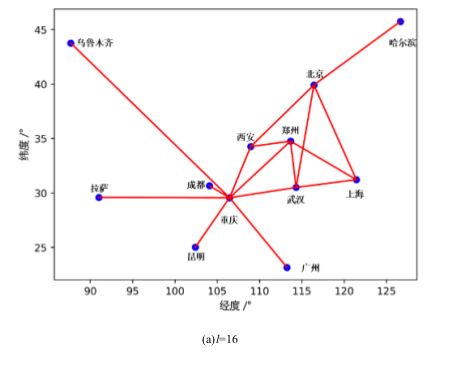
这个约束可以保证所有组成的集合(全集和空集除外)都与其他点是连通的.加入当前约束后得到的解如下图所示.
对于33条链路的是这样的.
2-2
第二问考虑到中转节点的问题,最初考虑在第一问的基础上进行拓展,为每条路段增加一个分配变量,也就是在这些变量中描述当前路段的资源是否进行分配,分配给谁.
然后通过增加约束条件约束分配必须满足题设需求.但是求解过程发现这样的求解占用太多资源.因此我们考虑将问题转化成为了一个层次优化的问题.在描述这个问题前,我们通过一些数学推导将问题稍作简化.
首先,中转通信的可行性分析.
一条线路进行中转的可行性,主要是由引入这些中转是否会带来目标(网络价值)的提升判断的.
如果引入这些中转可以将网络价值进行提升,那么系统将义不容辞的引入这些中转通信,如果不能,中转通信将一定不会被引入.
因此在引入的价值该如何度量呢?
看下图:
也就是说,当权重保持不变的情况下. 引入中转通信完全归结为节点的人口问题,对于三个节点的判断来说.当中间点城市的人口数足够小的情况下,引入中间节点通信是有好处的.
下面我们来进行更加复杂的分析.
当有多个城市需要占用同一个节点中转时,节点将为哪一个城市服务的问题.这个问题同样该从网络价值的角度分析.就是说我们要比较为谁服务可以获得更多的网络价值.
但是这个问题就没有前面的问题那样纯粹了,因为这将变成一个整体性的问题.也是一个规划问题.为了有效解决这个问题,本文件问题描述为一个两层的最优化问题的嵌套.
顶层的最优化问题负责寻找最优的网络路径,也就是像问题2-1一样的规划问题.第二个最优化问题在上层给出的路径的基础上寻找一个最优化的网络配置,配置最优化的中转节点情况.
在这种情况下,我们本文采用两层的架构,第一层使用遗传算法作为框架,第二层使用约束式求解器GUROBI.
2-3 第三问是自由式的问题,因此在这里不做分享
3
第三问由于太直接,没有太好的方法进行求解,所以直接上了遗传算法.
没有什么有效的数学模型可以将问题化简,大家有兴趣可以直接看我的代码.
代码:
问题求解的正确性我还没有作进一步的考证,
在这里发表一些想法只做讨论用.
代码我已经上传到了github: https://github.com/zangzelin/2018-Graduate-Mathematical-Modeling-Competition-B
希望觉得有帮助的同学,star 一下
---恢复内容结束---
# 2018研究生数学建模竞赛B题-光传送网建模与价值评估-竞赛总结这道赛题是有关通信方面的赛题,初步读题,感到第一问和第二问关系不大,第二问和第三问关系也不大,不过第一问和第三问有比较紧密的顺承关系.
1-1
第一问主要讨论在光纤通信环境下,与光信号传输有关的调制解调的误码率问题.在题设条件中,纠前误码率(BER)只与信噪比(SNR)有关.因此题目要求我们建立数学模型描述两者的关系.
对于该问题有两种思路:
- 建立机理模型
也就是通过对光纤中的入纤信号,与信号噪声进行概率描述,然后推导出出纤信号的概率描述,从而通过对概率密度函数的二重积分,直接计算出两者的解析关系.
- 实验模型
也就是使用计算机仿真的方式,通过大量的实验,模拟信号输入,编码,噪声输入,解码,计算误码率的过程,对误码率进行计算.根据大数定律,大量实验的结果会趋近于第一种思路的机理模型的解.
- 两种方法的比较
第一种方法有着更强的数学要求,但是推到的结果显示,最后的结果是一个正态分布函数的二重积分的加权和.计算这个函数的积分其实十分困难,还是要借助数值计算的工具或者查表.无法有效的得到一条表达式.
第二种方法较容易实现,但是在试验次数较小的情况下,得到的曲线会引入较大误差.造成求解曲线的不平滑.因此得到平滑的曲线需要花费较大的计算时间.在我的电脑上计算时间大概有半个小时.
在这里给出一张求解图.
1-2
第二问主要是对整个传输的光路进行建模,要考虑光在线缆中引入的噪声,光放大器引入的噪声,光在线缆中的功率衰减等因素,结合上文中算出的一个参数求解传输链路的段数.
在这里给出模型和结果.
结果
2-1
第二问似乎与第一问没有必然的联系,这是一个整数规划的问题,特别是在第一问中,这个证书规划非常的纯粹,因此可以直接建立整数规划的模型,使用相应的求解器进行求解.
我们将问题直接转化成了MIP问题,然后使用GUROBI工具进行求解.
转化成的问题如下图.
其中Cij 表示 i 节点与 j 节点之间的传输容量,可依据节点间的距离选择相应的传输格式,从而判断传输容量的大小。本文认为,若要使网络价值最大化,必须要以容量利用率最大为标准来分配传输格式。
λ ij 表示 i 节点与 j 节点之间链路的权重,M 为光传输网络的节点数。
H i ,H j 分别表示 i 节点和 j 节点的人口数。当所有节点的链接情况由决策
信息R ij 确定时,目标函数值中相应的未知变量可进一步求出并确定目标函数值.
约束中限制了网络连接数,和孤立链路数量.
值得一题的是孤立链路这个约束.
在一开始我们解出的解如下图:
可以看到,得到的解并不是一个连通的图.但是作为一个光纤网络来说,必然要求我们解出一个连通图.因此我们加入了孤立链路这个新的约束.
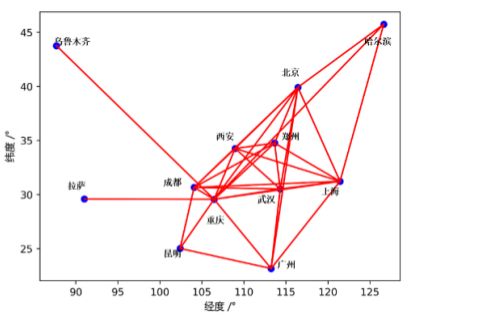
这个约束可以保证所有组成的集合(全集和空集除外)都与其他点是连通的.加入当前约束后得到的解如下图所示.
对于33条链路的是这样的.
2-2
第二问考虑到中转节点的问题,最初考虑在第一问的基础上进行拓展,为每条路段增加一个分配变量,也就是在这些变量中描述当前路段的资源是否进行分配,分配给谁.
然后通过增加约束条件约束分配必须满足题设需求.但是求解过程发现这样的求解占用太多资源.因此我们考虑将问题转化成为了一个层次优化的问题.在描述这个问题前,我们通过一些数学推导将问题稍作简化.
首先,中转通信的可行性分析.
一条线路进行中转的可行性,主要是由引入这些中转是否会带来目标(网络价值)的提升判断的.
如果引入这些中转可以将网络价值进行提升,那么系统将义不容辞的引入这些中转通信,如果不能,中转通信将一定不会被引入.
因此在引入的价值该如何度量呢?
看下图:
也就是说,当权重保持不变的情况下. 引入中转通信完全归结为节点的人口问题,对于三个节点的判断来说.当中间点城市的人口数足够小的情况下,引入中间节点通信是有好处的.
下面我们来进行更加复杂的分析.
当有多个城市需要占用同一个节点中转时,节点将为哪一个城市服务的问题.这个问题同样该从网络价值的角度分析.就是说我们要比较为谁服务可以获得更多的网络价值.
但是这个问题就没有前面的问题那样纯粹了,因为这将变成一个整体性的问题.也是一个规划问题.为了有效解决这个问题,本文件问题描述为一个两层的最优化问题的嵌套.
顶层的最优化问题负责寻找最优的网络路径,也就是像问题2-1一样的规划问题.第二个最优化问题在上层给出的路径的基础上寻找一个最优化的网络配置,配置最优化的中转节点情况.
在这种情况下,我们本文采用两层的架构,第一层使用遗传算法作为框架,第二层使用约束式求解器GUROBI.
2-3 第三问是自由式的问题,因此在这里不做分享
3
第三问由于太直接,没有太好的方法进行求解,所以直接上了遗传算法.
没有什么有效的数学模型可以将问题化简,大家有兴趣可以直接看我的代码.
代码:
问题求解的正确性我还没有作进一步的考证,
在这里发表一些想法只做讨论用.
代码我已经上传到了github: https://github.com/zangzelin/2018-Graduate-Mathematical-Modeling-Competition-B
希望觉得有帮助的同学,star 一下