串的模式匹配算法-KMP算法的演进

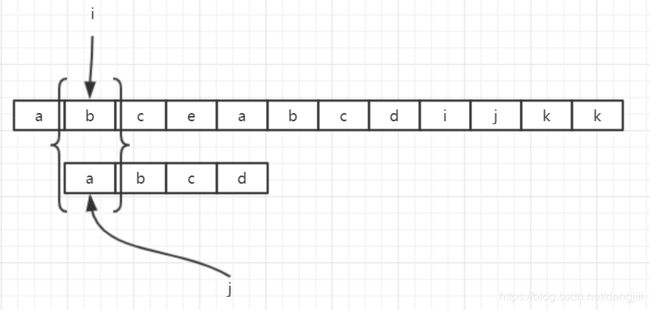
也就是平时所说的求子串位置的定位函数 Index(S,T,pos)，如下图所示，请子串abcd在字符串abceabcdijkl位置

通常的做法实现如下

1. 定义数据类型

   #define MAX_STRING_LEN 255
   
   // 下标为0存放串长度
   typedef unsigned char String[MAX_STRING_LEN + 1];
   

2. 定义字符串构建和字符串遍历的方法
   字符串构造， 其中字符数组第0位存储字符串长度

   Status Create(String &T, char str[])
   {
   	int index = 0;
   	while (str[index] != '\0')
   	{
   		T[index + 1] = str[index];
   		index++;
   	}
   	T[0] = index;
   	return OK;
   }
   

   子串位置的定位函数 Index(S,T,pos)

   int Index(String S, String T, int pos)
   {
   
   	if (pos < 1 || pos > S[0])
   	{
   		return FALSE;
   	}
   
   	int i = pos;
   	int j = 1;
   
   	while (i <= S[0] && j <= T[0])
   	{
   		if (S[i] == T[j])
   		{
   			i++;
   			j++;
   		}
   		else
   		{
   			i = i - j + 2;
   			j = 1;
   		}
   
   	}
   
   	if (j > T[0])
   	{
   		return i - T[0];
   	}
   
   	return FALSE;
   }
   

3. 测试

int main()
{
	String T;
	Create(T, "abceabcdijkl");
	Traverse(T, visit);

	String T2;
	Create(T2, "abcd");
	Traverse(T2, visit);
	printf("index=%d\n", Index(T, T2, 1));

	return 0;
}

测试结果该abcd字符串的位置在abceabcdijkl第5位

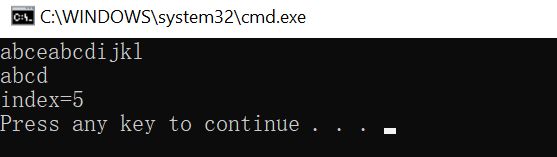
完成代码链接 CODE: 求子串位置的定位函数 Index(S,Tpos)

以上算法弊端分析

当i=4，j=4时，e不等于d，上面算法将出现回溯

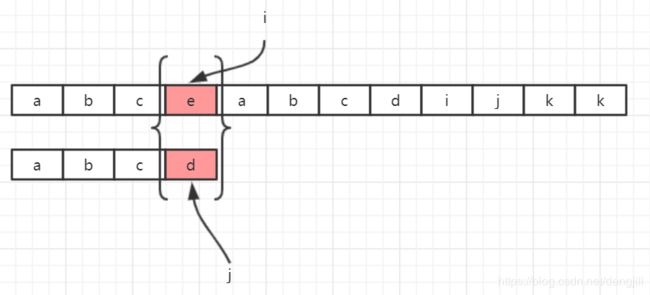
也就是说，i的值需要重置到i=2，如果回溯，那么将重复做无用功，也就说，b，c开始匹配，肯定是匹配不成功的。那么我们有没有办法不回溯呢

KMP算法

为了解决主串不回溯的问题，将引入KMP算法，kmp是对模式匹配的一种改进算法，本身并不是很复杂

过程演示

下面将演示一下过程，主串ababcabcacbab，匹配串abcac

第一次匹配失败（主串i不变，不回溯，j = 1）

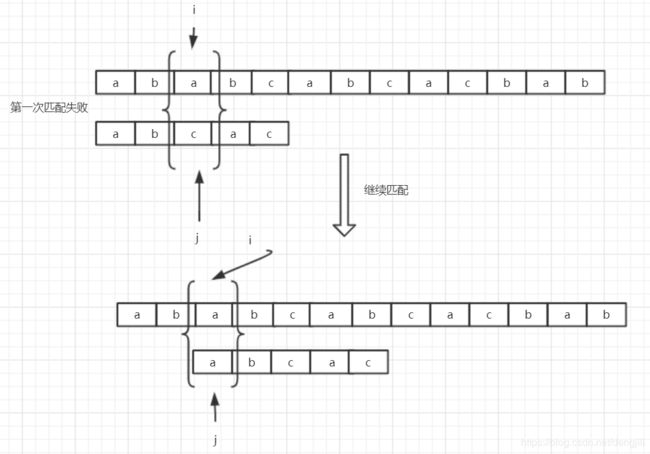
第二次匹配失败（主串i不变，不回溯，j = 2）

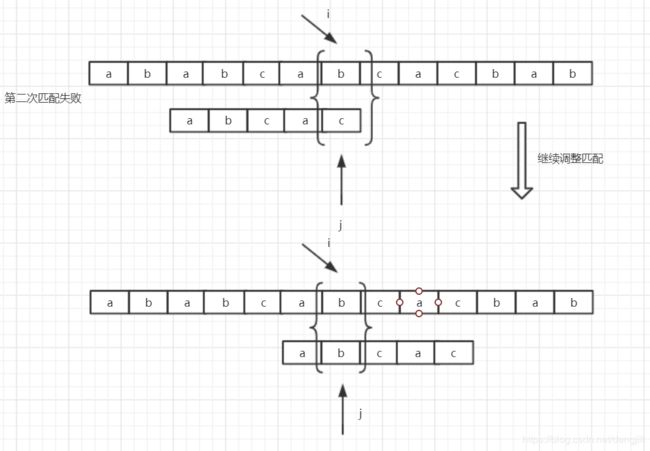
从上图演过可以看出，主串i主需要遍历一次就可以了，也就是说i不需要回溯

匹配失败，匹配串j的取值计算（匹配串移动距离计算）

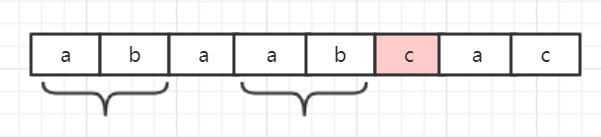
kmp的改进实际上也只是在找匹配串匹配失败后，匹配串移动距离，如下图所示，当b不等于c以后，那么匹配串abcac将找出哪一个字符串继续与主串的b继续比较

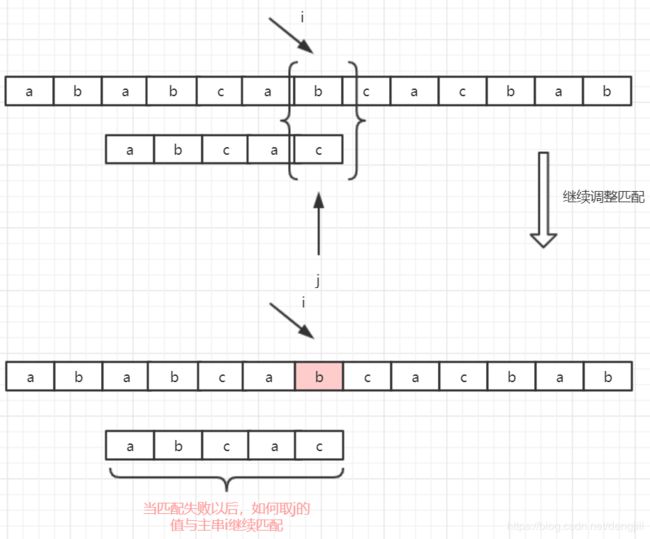
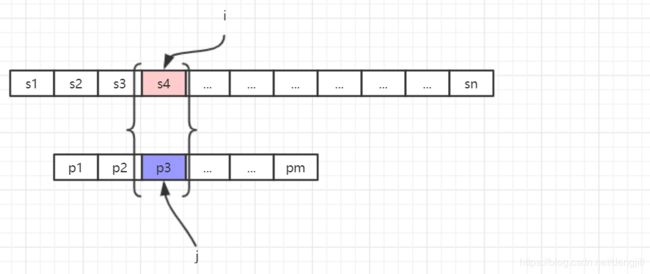
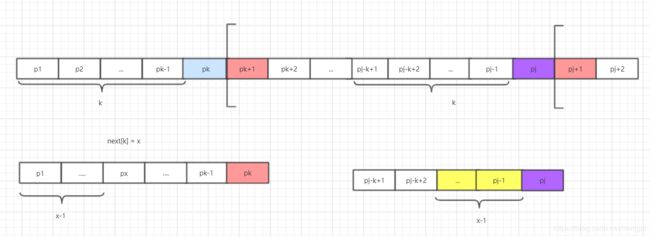
下面我们将来讨论匹配串右移的问题，现在讨论一般情况。假设主串为s12…sn,模式串为p1p2…pm,从上例的分析可知,为了实现改进算法,需要解决下述问题:当匹配过程中产生失配(即si≠pj)时,模式串向右滑动可行的距离多远,换句话说,当主串中第i个字符与模式中第j个字符失配(即比较不等)时,主串中第i个字符(i指针不回溯)应与模式中哪个字符再比较?

1. 假设当前s4 不等于p3
   
2. 假设下一个与si匹配的字符串为pk
   
   在k的左面，和i的左面，一定存在等式

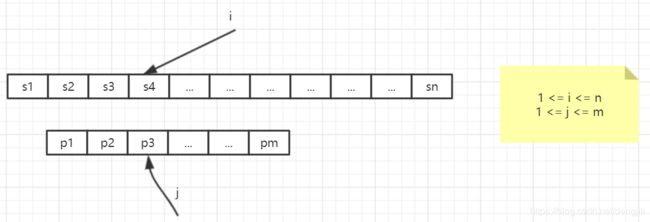
前k位匹配恒等：p1p2...pk-1=si-k+1si-k+2...si-1 （1-1）

也就是对应上述中的p1=s3

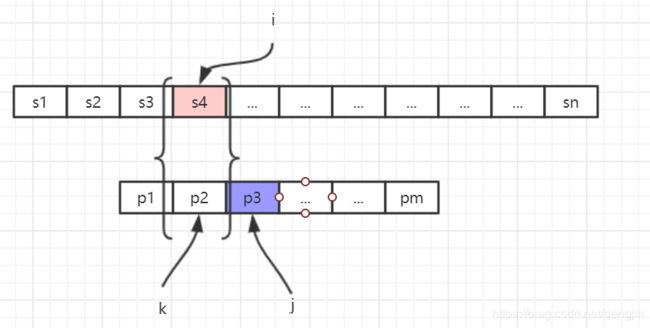
在j的左面，一定存在等式
后k位匹配恒等：pj-k+1pj-k+2...pj-1=si-k+1si-k+2...si-1 （1-2）

由式(1-1)和式(1-2)推得下列等式
p1p2...pk-1=pj-k+1pj-k+2...pj-1（1-3）

从（1-3）中可以看出，对于k的取值，已经完全和主串中的i无关，寻找这个k有多长（匹配串移动距离），变成了计算匹配串前k-1位匹配恒等 == 后k-1位匹配相等的最大值

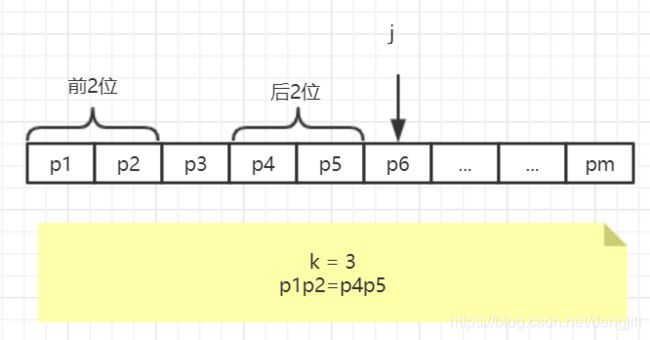
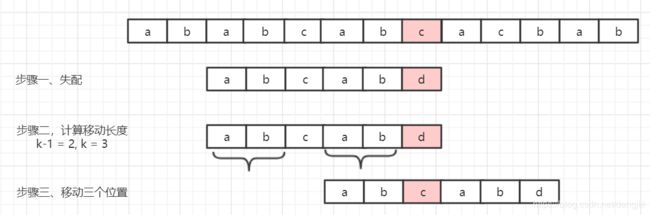
如图所示，假设匹配串匹配到p6（j=6失配），而根据匹配串p1p2=p4p5，k=3，那么移动距离直接将j = k，j = 3。实际字符串演示

匹配串移动距离计算算法（理论计算）

给定匹配串abaabcac,j为当前失配的下标，k为移动的距离
下面给出k的计算逻辑

1. j = 1，k = 0（也就说第一个匹配失效，需要移动主串了，而不移动匹配串）
2. 在j的下标之前的匹配串（也就说sub(T, 0, j - 1)）满足p1p2...pk-1=pj-k+1pj-k+2...pj-1（1-3）,取max(k)
3. 不满足前面两条，取值为1

给出三个个例子演示，帮助理解

• j = 1，满足第一条，取值为0
• j = 2或者3，不能满足第一条或第二条，取值为1
• j=6匹配失败，满足第二条
  p1p2=p4p5, k-1=2, k= 3
  
  下面给出所有计算结果

j	1	2	3	4	5	6	7	8
匹配串	a	b	a	a	b	c	a	c
k	0	1	1	2	2	3	1	2

有了以上移动数据，我们可以看一个具体的匹配过程

匹配串移动距离计算算法（算法实现）

KMP算法是在已知模式串的next函数值的基础上执行的,那么,如何求得模式串的
移动距离值呢?

我们定义函数：next[j] = k

1. 由于上面理论定义可以得知next[1] = 0

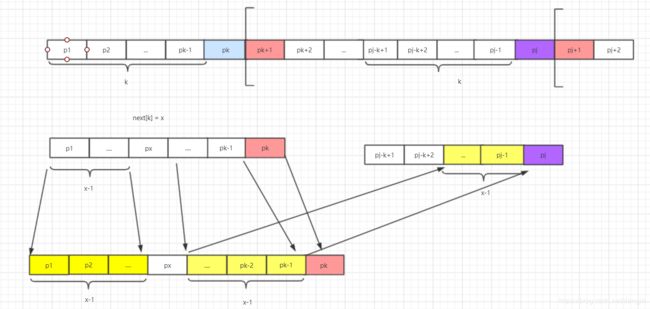
假设next[j]=k,模式串中存在下列关系:p1p2...pk-1=pj-k+1pj-k+2...pj-1（1-3），上述已经证明。也就说求next[j]是求pk左的字符串，与pj左面的字符串是否相等，最终求出的k值为：匹配字符串的长度+1，也就是pk的下标， k，即next[j] = k

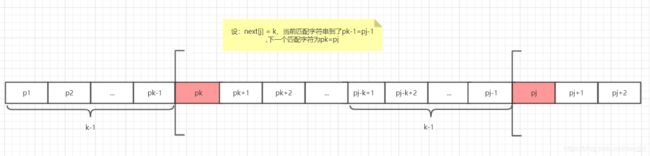
此时求next[j+1]=?可能有两种情况（此时是比较pj结点与pk是否相等）:

2. 当pk = pj,则p1p2...pk=pj-k+1pj-k+2...pj，则next[j+1]=next[j] + 1(1-4)，
   
   这个比较好理解，如果pk = pj,那么匹配相等长度比上一个结点+1
   

3. 当pk 不等于 pj,则p1p2...pk 不等于 pj-k+1pj-k+2...pj，那么我们是否能够找出比k小的值x（即x < k），满足p1p2...px=pj-x+1pj-x+2...pj（1-4）。也就说，当我们匹配失败的时候，需要将返回缩小匹配，本质上也是进行递归求值，也是求更小的移动距离。

图中的黄色部份都是相等。因为以上两个等式

• p1p2...pk-1=pj-k+1pj-k+2...pj-1（1-3）
• p1p2...px=pj-x+1pj-x+2...pj（1-4）

我们可以推导出如图中关系

此时，

1. 如果px = pj，那么只要重复第一个步骤规则，也就说所next[j+1] = next[k] + 1;
   
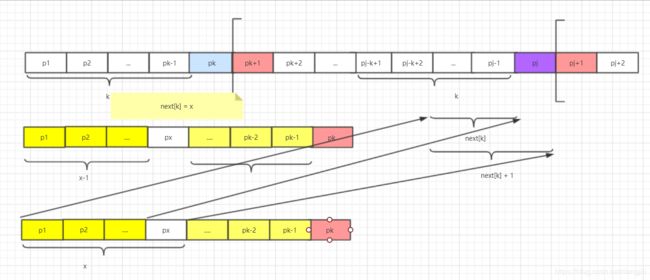
2. 否则，重复上面一个步骤，也就说说next[j+1] = next[…next[next[k]]] + 1;一直不停的计算下去，直到next[1] = 0，递归结束;

至此。理论阶段结束

KMP算法代码实现

next函数值计算

计算字符串bbabbxbbabbyx的next函数值

#include 
#include 
#include "string.h"

void visit(String T)
{
	for (int i = 1; i <= T[0]; i++)
	{
		printf("%-3c", T[i]);
	}
	printf("\n");
}

void get_next(String T, int next[])
{
	int i = 1;
	int j = 0;

	next[1] = 0;

	while (i < T[0])
	{
		if (j == 0 || T[i] == T[j])
		{
			i++;
			j++;
			next[i] = j;
		}
		else
		{
			j = next[j];
		}
	}
}


int main()
{
	String T;
	Create(T, "bbabbxbbabbyx");
	Traverse(T, visit);

	int next[MAX_STRING_LEN + 1];
	get_next(T, next);

	for (int j = 1; j <= T[0]; j++) 
	{
		printf("%-2d ", j);
	}
	printf("\n");
	for (int j = 1; j <= T[0]; j++) 
	{
		printf("%-2d ", next[j]);
	}
	printf("\n");

	return 0;
}

完整代码链接：code
测试结果

b  b  a  b  b  x  b  b  a  b  b  y  x
1  2  3  4  5  6  7  8  9  10 11 12 13
0  1  2  1  2  3  1  2  3  4  5  6  1
Press any key to continue . . .

完整的kmp算法实现

关键代码改进

int Index_kmp(String S, String T, int pos)
{
	if (pos < 1 || pos > S[0])
	{
		return FALSE;
	}

	// 计算next函数值
	int next[MAX_STRING_LEN + 1];
	get_next(T, next);

	int i = pos;
	int j = 1;

	while (i <= S[0] && j <= T[0])
	{
		// 因为next[1] = 0; 所以添加递归结束条件 j == 0
		if (j == 0 || S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
		}

	}

	if (j > T[0])
	{
		return i - T[0];
	}

	return FALSE;
}

完整代码链接：code
测试结果

aaaaabbbbbfffff
abb
index=5
Press any key to continue . . .