Codeforces Round #503 (by SIS, Div. 2) 题解
额,第一次现场打cf(居然没掉rating),还是暴露了许多问题,自己的基础不够扎实(连暴力分都没拿全),下面是自己写的ABCD的题解(E题题解已更新):
A. New Building for SIS
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
You are looking at the floor plan of the Summer Informatics School's new building. You were tasked with SIS logistics, so you really care about travel time between different locations: it is important to know how long it would take to get from the lecture room to the canteen, or from the gym to the server room.
The building consists of n towers, h floors each, where the towers are labeled from 1 to n, the floors are labeled from 1 to h. There is a passage between any two adjacent towers (two towers i and i + 1 for all i: 1 ≤ i ≤ n - 1) on every floor x, where a ≤ x ≤ b. It takes exactly one minute to walk between any two adjacent floors of a tower, as well as between any two adjacent towers, provided that there is a passage on that floor. It is not permitted to leave the building.
![]()
The picture illustrates the first example.
You have given k pairs of locations (ta, fa), (tb, fb): floor fa of tower ta and floor fb of tower tb. For each pair you need to determine the minimum walking time between these locations.
Input
The first line of the input contains following integers:
- n: the number of towers in the building (1 ≤ n ≤ 108),
- h: the number of floors in each tower (1 ≤ h ≤ 108),
- a and b: the lowest and highest floor where it's possible to move between adjacent towers (1 ≤ a ≤ b ≤ h),
- k: total number of queries (1 ≤ k ≤ 104).
Next k lines contain description of the queries. Each description consists of four integers ta, fa, tb, fb (1 ≤ ta, tb ≤ n, 1 ≤ fa, fb ≤ h). This corresponds to a query to find the minimum travel time between fa-th floor of the ta-th tower and fb-th floor of the tb-th tower.
Output
For each query print a single integer: the minimum walking time between the locations in minutes.
Example
Input
Copy
3 6 2 3 3
1 2 1 3
1 4 3 4
1 2 2 3
Output
Copy
1
4
2
好吧是道大模拟(我不会告诉你我第一遍把k打成n然后WA3)
#include
#include
#include
#include
#include
#include
#include
#include
B. Badge
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
In Summer Informatics School, if a student doesn't behave well, teachers make a hole in his badge. And today one of the teachers caught a group of n
students doing yet another trick.
Let's assume that all these students are numbered from 1
to n. The teacher came to student a and put a hole in his badge. The student, however, claimed that the main culprit is some other student pa
.
After that, the teacher came to student pa
and made a hole in his badge as well. The student in reply said that the main culprit was student ppa
.
This process went on for a while, but, since the number of students was finite, eventually the teacher came to the student, who already had a hole in his badge.
After that, the teacher put a second hole in the student's badge and decided that he is done with this process, and went to the sauna.
You don't know the first student who was caught by the teacher. However, you know all the numbers pi
. Your task is to find out for every student a, who would be the student with two holes in the badge if the first caught student was a
.
Input
The first line of the input contains the only integer n
(1≤n≤1000
) — the number of the naughty students.
The second line contains n
integers p1, ..., pn (1≤pi≤n), where pi indicates the student who was reported to the teacher by student i
.
Output
For every student a
from 1 to n print which student would receive two holes in the badge, if a
was the first student caught by the teacher.
Examples
Input
Copy
3
2 3 2
Output
Copy
2 2 3
Input
Copy
3
1 2 3
Output
Copy
1 2 3
Note
The picture corresponds to the first example test case.
When a=1
, the teacher comes to students 1, 2, 3, 2, in this order, and the student 2
is the one who receives a second hole in his badge.
When a=2
, the teacher comes to students 2, 3, 2, and the student 2 gets a second hole in his badge. When a=3, the teacher will visit students 3, 2, 3 with student 3
getting a second hole in his badge.
For the second example test case it's clear that no matter with whom the teacher starts, that student would be the one who gets the second hole in his badge.
一开始看成了NOIP2015D1T2,后来看见良心数据,果断O(n^2)模拟
(据某位不愿意透露姓名的现场16名的dalao透露他一开始写个O(n)的算法后来才发现O(n^2)可过QAQ)
#include
#include
#include
#include
#include
#include
#include
#include
C. Elections
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
As you know, majority of students and teachers of Summer Informatics School live in Berland for the most part of the year. Since corruption there is quite widespread, the following story is not uncommon.
Elections are coming. You know the number of voters and the number of parties — n
and m respectively. For each voter you know the party he is going to vote for. However, he can easily change his vote given a certain amount of money. In particular, if you give i-th voter ci
bytecoins you can ask him to vote for any other party you choose.
The United Party of Berland has decided to perform a statistical study — you need to calculate the minimum number of bytecoins the Party needs to spend to ensure its victory. In order for a party to win the elections, it needs to receive strictly more votes than any other party.
Input
The first line of input contains two integers n
and m (1≤n,m≤3000
) — the number of voters and the number of parties respectively.
Each of the following n
lines contains two integers pi and ci (1≤pi≤m, 1≤ci≤109
) — the index of this voter's preferred party and the number of bytecoins needed for him to reconsider his decision.
The United Party of Berland has the index 1
.
Output
Print a single number — the minimum number of bytecoins needed for The United Party of Berland to win the elections.
Examples
Input
Copy
1 2
1 100
Output
Copy
0
Input
Copy
5 5
2 100
3 200
4 300
5 400
5 900
Output
Copy
500
Input
Copy
5 5
2 100
3 200
4 300
5 800
5 900
Output
Copy
600
Note
In the first sample, The United Party wins the elections even without buying extra votes.
In the second sample, The United Party can buy the votes of the first and the fourth voter. This way The Party gets two votes, while parties 3
, 4 and 5 get one vote and party number 2
gets no votes.
In the third sample, The United Party can buy the votes of the first three voters and win, getting three votes against two votes of the fifth party.
额…… 日常不会写暴力,看到数据范围还以为是dp(果然还是菜啊)
暴力枚举1政党赢得选举时所获得的选票数(记为win),首先将选票数多于win的政党买他们最便宜的选票。如果此时1政党的选票数还未达到win,就买所有剩下选票中最便宜的(看起来好简单可我就是想不到)
#include
#include
#include
#include
#include
#include
#include
#include D. The hat
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
This is an interactive problem.
Imur Ishakov decided to organize a club for people who love to play the famous game «The hat». The club was visited by n students, where n is even. Imur arranged them all in a circle and held a draw to break the students in pairs, but something went wrong. The participants are numbered so that participant i and participant i + 1 (1 ≤ i ≤ n - 1) are adjacent, as well as participant n and participant 1. Each student was given a piece of paper with a number in such a way, that for every two adjacent students, these numbers differ exactly by one. The plan was to form students with the same numbers in a pair, but it turned out that not all numbers appeared exactly twice.
As you know, the most convenient is to explain the words to the partner when he is sitting exactly across you. Students with numbers i and ![]() sit across each other. Imur is wondering if there are two people sitting across each other with the same numbers given. Help him to find such pair of people if it exists.
sit across each other. Imur is wondering if there are two people sitting across each other with the same numbers given. Help him to find such pair of people if it exists.
You can ask questions of form «which number was received by student i?», and the goal is to determine whether the desired pair exists in no more than 60 questions.
Input
At the beginning the even integer n (2 ≤ n ≤ 100 000) is given — the total number of students.
You are allowed to ask no more than 60 questions.
Output
To ask the question about the student i (1 ≤ i ≤ n), you should print «? i». Then from standard output you can read the number ai received by student i ( - 109 ≤ ai ≤ 109).
When you find the desired pair, you should print «! i», where i is any student who belongs to the pair (1 ≤ i ≤ n). If you determined that such pair doesn't exist, you should output «! -1». In both cases you should immediately terminate the program.
The query that contains your answer is not counted towards the limit of 60 queries.
Please make sure to flush the standard output after each command. For example, in C++ use function fflush(stdout), in Java call System.out.flush(), in Pascal use flush(output) and stdout.flush() for Python language.
Hacking
Use the following format for hacking:
In the first line, print one even integer n (2 ≤ n ≤ 100 000) — the total number of students.
In the second line print n integers ai ( - 109 ≤ ai ≤ 109) separated by spaces, where ai is the number to give to i-th student. Any two adjacent elements, including n and 1, must differ by 1 or - 1.
The hacked solution will not have direct access to the sequence ai.
Examples
Input
Copy
8
2
2
Output
Copy
? 4
? 8
! 4
Input
Copy
6
1
2
3
2
1
0Output
Copy
? 1
? 2
? 3
? 4
? 5
? 6
! -1Note
Input-output in statements illustrates example interaction.
In the first sample the selected sequence is 1, 2, 1, 2, 3, 4, 3, 2
In the second sample the selection sequence is 1, 2, 3, 2, 1, 0.
交互题QAQ
看不懂英文是硬伤
题意:有n个人,每个人手上有一个数字,保证相邻两个人的数字相差1,请问是否存在相对的两个人手上有相同的数字。
题解:
记第i个人手上的数字为ai
首先特判出无解:n%4==2 原因是这时从a1走到an/2必定走过奇数个人,所以a1-an/2一定是个奇数,而又由于相邻两个人的数字只差1,所以ai与a(i+n/2)的差必定是个奇数(它与相邻那对数之差只能相差-2或0或2),而相同的两数差只能为0,是偶数。所以命题得证。
理解了上面接下来就好处理了,预处理出a1-an/2,然后再进行二分查找,如果两者同好则取右半边,否则取左半边
#include
#include
#include
#include
#include
#include
#include
#include
-------------------------------------------------------update---------------------------------------------------------------------------------------------------------
E. Sergey's problem
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Sergey just turned five years old! When he was one year old, his parents gave him a number; when he was two years old, his parents gave him an array of integers. On his third birthday he received a string. When he was four, his mother woke him up in a quiet voice, wished him to be a good boy and gave him a rooted tree. Today he celebrates his birthday again! He found a directed graph without loops as a present from his parents.
Since Sergey is a very curious boy, he immediately came up with a thing to do. He decided to find a set Q
of vertices in this graph, such that no two vertices x,y∈Q are connected by an edge, and it is possible to reach any vertex z∉Q from some vertex of Q
in no more than two moves.
After a little thought, Sergey was able to solve this task. Can you solve it too?
A vertex y
is reachable from a vertex x in at most two moves if either there is a directed edge (x,y), or there exist two directed edges (x,z) and (z,y) for some vertex z
.
Input
The first line of input contains two positive integers n
and m (1≤n≤1000000, 1≤m≤1000000
) — the number of vertices and the number of edges in the directed graph.
Each of the following m
lines describes a corresponding edge. Each one contains two integers ai and bi (1≤ai,bi≤n, ai≠bi) — the beginning and the end of the i
-th edge. The graph may contain multiple edges between the same pair of vertices.
Output
First print the number k
— the number of selected vertices. Then print k
distinct integers — the indices of the selected vertices.
If multiple answers exist you can output any of them. In particular, you don't have to minimize the number of vertices in the set. It is guaranteed, that there is always at least one valid set.
Examples
Input
Copy
5 4
1 2
2 3
2 4
2 5
Output
Copy
4
1 3 4 5
Input
Copy
3 3
1 2
2 3
3 1
Output
Copy
1
3
Note
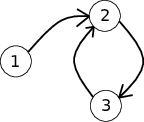
In the first sample, the vertices 1,3,4,5
are not connected. The vertex 2 is reachable from vertex 1
by one edge.
In the second sample, it is possible to reach the vertex 1
in one move and the vertex 2
in two moves.
The following pictures illustrate sample tests and their answers.
洛谷上给的居然是NOI的标签,可怕啊……
主要还是思路的问题
考虑将图中的每一个点删去,记当前删掉的点为u,则先将u压入栈中,再将点u以及所有u连向的点删去,再从剩下的图中重复进行上述操作。这一步几乎(重点)可以避免所求点集中有互相联通的点。
接下来开始进行弹栈操作。对于当前弹出的点u,如果所有连向u的点都未加入答案中,则将u加入答案中,否则就不加入。
因为假设答案集合中有一个点v可以到达弹出的点u,则v可以通过一步走向点u,同时对于u所连向的点,v都可以通过先走u的方式走向那些点,满足题目的要求2 。
那么为什么要用栈而不是其他数据结构呢?因为可能出现这种情况:1及其连向的点首先被删去。接下来的2号节点可能会连向1号节点,但是由于操作顺序的原因1无法弹出。所以采用栈这种数据结构。
那么如何实现呢?
对于第一步直接记一个del数组表示是否被删除,同时将现在操作的点压入栈中。
对于第二步,我们可以在读入时进行反向建图,同时通过一个used数组来表示是否已经进入答案点集中。
这样就可以解决啦QAQ
#include
#include
#include
#include
#include
#include
#include
#include
#include 话说这个人的生日礼物也真是清奇啊