莫烦pytorch学习笔记6

1.生成对抗网路gan

1.1 介绍

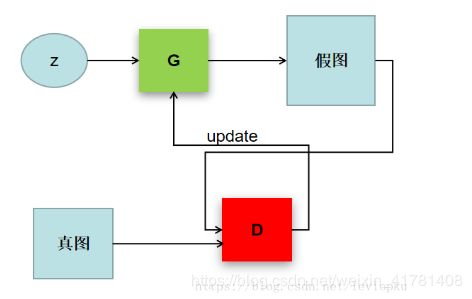
生成式对抗网络（GAN, Generative Adversarial Networks ）是一种深度学习模型，是近年来复杂分布上无监督学习最具前景的方法之一。模型通过框架中（至少）两个模块：生成模型（Generative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。原始 GAN 理论中，并不要求 G 和 D 都是神经网络，只需要是能拟合相应生成和判别的函数即可。但实用中一般均使用深度神经网络作为 G 和 D 。一个优秀的GAN应用需要有良好的训练方法，否则可能由于神经网络模型的自由性而导致输出不理想。

1.2GAN的原理

这里介绍的是原生的GAN算法，虽然有一些不足，但提供了一种生成对抗性的新思路。

理解GAN的两大护法G和D

G是generator，生成器: 负责凭空捏造数据出来

D是discriminator，判别器: 负责判断数据是不是真数据

这样可以简单的看作是两个网络的博弈过程。在最原始的GAN论文里面，G和D都是两个多层感知机网络。首先，注意一点，GAN操作的数据不一定非得是图像数据，不过为了更方便解释，我在这里用图像数据为例解释以下GAN：

import torch
import torch.nn as nn
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible
np.random.seed(1)
# Hyper Parameters
BATCH_SIZE = 64
LR_G = 0.0001           # learning rate for generator
LR_D = 0.0001           # learning rate for discriminator
N_IDEAS = 5             # think of this as number of ideas for generating an art work (Generator)
ART_COMPONENTS = 15     # it could be total point G can draw in the canvas
PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)])
# print(PAINT_POINTS)

# show our beautiful painting range
plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
plt.legend(loc='upper right')
plt.show()

def artist_works():     # painting from the famous artist (real target)
    a = np.random.uniform(1, 2, size=BATCH_SIZE)[:, np.newaxis]
    paintings = a * np.power(PAINT_POINTS, 2) + (a-1)
    paintings = torch.from_numpy(paintings).float()
    return Variable(paintings)

G = nn.Sequential(                      # Generator
    nn.Linear(N_IDEAS, 128),            # random ideas (could from normal distribution)
    nn.ReLU(),
    nn.Linear(128, ART_COMPONENTS),     # making a painting from these random ideas
)

D = nn.Sequential(                      # Discriminator
    nn.Linear(ART_COMPONENTS, 128),     # receive art work either from the famous artist or a newbie like G
    nn.ReLU(),
    nn.Linear(128, 1),
    nn.Sigmoid(),                       # tell the probability that the art work is made by artist
)

opt_D = torch.optim.Adam(D.parameters(), lr=LR_D)
opt_G = torch.optim.Adam(G.parameters(), lr=LR_G)

for step in range(10000):
    artist_paintings = artist_works()           # real painting from artist
    G_ideas = Variable(torch.randn(BATCH_SIZE, N_IDEAS))    # random ideas
    G_paintings = G(G_ideas)                    # fake painting from G (random ideas)

    prob_artist0 = D(artist_paintings)          # D try to increase this prob
    prob_artist1 = D(G_paintings)               # D try to reduce this prob

    D_loss = - torch.mean(torch.log(prob_artist0) + torch.log(1. - prob_artist1))
    G_loss = torch.mean(torch.log(1. - prob_artist1))

    opt_D.zero_grad()
    D_loss.backward(retain_graph=True)      # retain_variables for reusing computational graph
    opt_D.step()

    opt_G.zero_grad()
    G_loss.backward()
    opt_G.step()

    if step % 1000 == 0:  # plotting
        plt.cla()
        plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0], c='#4AD631', lw=3, label='Generated painting',)
        plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
        plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
        plt.text(-.5, 2.3, 'D accuracy=%.2f (0.5 for D to converge)' % prob_artist0.data.numpy().mean(), fontdict={'size': 15})
        plt.text(-.5, 2, 'D score= %.2f (-1.38 for G to converge)' % -D_loss.data.numpy(), fontdict={'size': 15})
        plt.ylim((0, 3));plt.legend(loc='upper right', fontsize=12);plt.draw();plt.pause(0.01)
        plt.show()

1.3 L1正则化和L2正则化实现

class MLP(torch.nn.Module):
    def __init__(self):
        super(MLP,self).__init__()
        self.linear1 = torch.nn.Linear(128,32)
        self.linear2 = torch.nn.Linear(32,16)
        self.linear3 = torch.nn.Linear(16,2)
    def forward(self,x):
        out1 = F.relu(self.linear1(x))
        out2 = F.relu(self.linear2(out1))
        out = F.relu(self.linear3(out2))
        return out,out1,out2
    
def l1_penalty(var):
    return torch.abs(var).sum()

def l2_penalty(var):
    return torch.sqrt(torch.pow(var,2).sum())

batchsize = 4

lambda1,lambda2  = 0.5,0.01

for i in range(1000):
    model = MLP()
    optimizer = torch.optim.SGD(model.parameters(),lr =1e-4)
    inputs = torch.rand(batchsize,128)
    targets = torch.ones(batchsize).long()
    
    optimizer.zero_grad()
    outputs,out1,out2 = model(inputs)
    
    cross_entropy_loss = F.cross_entropy(outputs,targets)
    l1_regularization = lambda1 * l1_penalty(out1)
    l2_regularization = lambda2 * l2_penalty(out2)
    
    loss = cross_entropy_loss + l1_regularization + l2_regularization
    print(i,loss.item())
    loss.backward()
    optimizer.step()
    

参考：
https://blog.csdn.net/Heitao5200/article/details/90404177
https://blog.csdn.net/leviopku/article/details/81292192