算法导论（一）：快速排序与随机化快排

排序算法是算法学习的第一步，想当初我学的第一个算法就是选择排序，不过当时很长一段时间我都不清楚我到底用的是选择还是冒泡还是插入。只记得两个for一个if排序就完成了。

再后来更系统地接触算法，才发现那才是排序算法队伍中小小而基本的一员。

买的《算法导论》一直没有认真地看一看，下来要找实习找工作，为了做准备，也是为了复习一下算法，便扒出来好好学一学，并做一些记录，免得我金鱼般的记忆使我看了和没看一样。

快速排序

快速排序用到了分治思想，同样的还有归并排序。乍看起来快速排序和归并排序非常相似，都是将问题变小，先排序子串，最后合并。不同的是快速排序在划分子问题的时候经过多一步处理，将划分的两组数据划分为一大一小，这样在最后合并的时候就不必像归并排序那样再进行比较。但也正因为如此，划分的不定性使得快速排序的时间复杂度并不稳定。

快速排序的期望复杂度是O(nlogn)，但最坏情况下可能就会变成O(n^2)，最坏情况就是每次将一组数据划分为两组的时候，分界线都选在了边界上，使得划分了和没划分一样，最后就变成了普通的选择排序了。

快速排序分为三步分治过程，划分，解决，合并。

分解是将输入数组A[l..r]划分成两个子数组的过程。选择一个p，使得a被划分成三部分，分别是a[l..p-1]，a[p]和a[p+1..r]。并且使得a[l..p-1]中的元素都小于等于（或大于等于）a[p]，同时a[p]小于等于（或大于等于）a[p+1..r]中的所有元素。

解决是调用递归程序，解决分解中划分生成的两个子序列。

合并是递归到最深层，已经不能再划分成更小的子序列了，便开始合并。因为在分解的时候已经比较过大小，每一个父序列分解而来的两个子序列不仅是有序的，而且合并成一个序列之后还是有序的。因为快排可以在输入数组上进行操作，所以合并这一步不需要编写代码。

《算法导论》上称这样的排序为原址排序，即在原数组上操作就可以完成排序，不需要临时数组。

书上的代码非常简洁巧妙，我就不把书上的伪代码照抄上来了，这里给出Java的实现代码以供参考：

//快速排序
public static void QuickSort(int[] a, int left, int right) {
    if (left < right) {
        int p = partition(a, left, right);
        QuickSort(a, left, p - 1);
        QuickSort(a, p + 1, right);
    }
}

//快速排序数组划分
private static int partition(int[] a, int left, int right) {
    int x = a[right];
    int p = left - 1;
    for (int i = left; i < right; i++) {
        if (a[i] <= x) {
            p++;
            swap(a, p, i);
        }
    }
    swap(a, p+1, right);
    return p+1;
}

其中的swap函数如下：

//交换数组a中的a[i]和a[j]
private static void swap(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}

QuickSort(int[] a,int left,int right)函数没什么好说的，设置递归边界，接下来递归处理左序列，再处理右序列。

下来的partition(int[] a, int left, int right)就比较有意思了。

int x = a[right];这行代码选中一个主元，这里我们每次选择的都是当前序列中最右边那个。int p = left - 1;这行代码保存了一个变量p，用来记录比主元小的所有元素中，在序列中存放的位置最靠右的那个。接下来是个循环，从当前序列的第一个循环到倒数第二个（right-1）元素，来进行和主元比较。因为最后一个已经是主元了，所以就没有必要循环到right了。循环里面先是一个比较if (a[i] <= x)。这里写的是小于等于，更改这个就可以改变序列式由小到大还是由大到小排列。这里则是由小到大排列。如果进入了if语句，则说明a[i]（当前元素）比主元小，还记得之前的变量p吗，保存着比主元小的元素最右边的位置，这里先p++，接着把a[i]和a[p]交换，就是说把a[p]右边的元素和当前元素换位置。a[p]右边的元素是什么呢？可能就是当前元素，也可能是比主元大的元素。这样，就完成了比主元小的元素的处理。

可是如果a[i]>x呢，则不进入if执行这两行代码，也就是不动那个比主元大的元素。

这样直到循环结束，整个序列就变成了三部分，从a[left..p]是比主元小的元素，a[p+1..right-1]是比主元大的元素，a[right]则是主元。而我们划分的目的是将主元放在这两个序列的中间，则再执行一行语句swap(a, p+1, right);，将主元和比它大序列的第一个元素互换位置，就大功告成了。

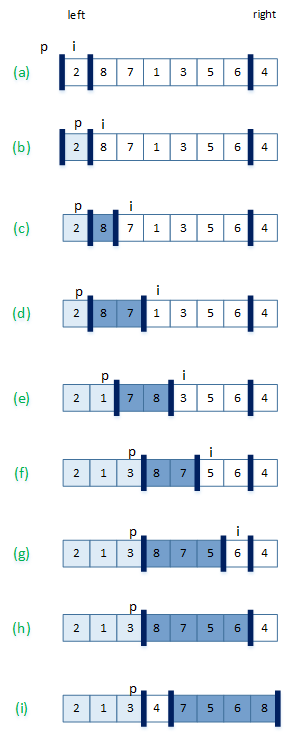
书上的图解非常的清晰：（标号是根据上面代码所标，和书上不太一样，但意思是一样的）

这张图描述了一次划分。浅蓝色部分是不大于主元的部分，深蓝色部分是大于主元的部分。没有颜色的是还未处理的元素，最后的元素则是主元。

快速排序的主要内容差不多就这些了，书上接下来证明了快速排序的正确性，以及计算了其时间复杂度。之后讨论了划分的不平衡性所导致的性能退化。对一个排好序的序列使用上述快排，时间复杂度为O(n^2)，而插入排序则仅为O(n)。因此便有了随机化快速排序的出现。

快速排序的随机化版本

上面版本的快排在选取主元的时候，每次都选取最右边的元素。当序列为有序时，会发现划分出来的两个子序列一个里面没有元素，而另一个则只比原来少一个元素。为了避免这种情况，引入一个随机化量来破坏这种有序状态。

在随机化的快排里面，选取a[left..right]中的随机一个元素作为主元，然后再进行划分，就可以得到一个平衡的划分。

实现起来其实只需要对上面的代码做小小的修改就可以了。

//快速排序的随机化版本，除了调用划分函数不同，和之前快排的代码结构一模一样
public static void RandomQuickSort(int[] a, int left, int right) {
    if (left < right) {
        int p = randomPartition(a, left, right);
        RandomQuickSort(a, left, p - 1);
        RandomQuickSort(a, p + 1, right);
    }
}

//随机化划分
public static int randomPartition(int[] a, int left, int right) {
    int r = random.nextInt(right - left) + left; //生成一个随机数，即是主元所在位置
    swap(a, right, r); //将主元与序列最右边元素互换位置，这样就变成了之前快排的形式。
    return partition(a, left, right); //直接调用之前的代码
}

这里的random是一个已经初始化过的Random的静态对象。

随机化快排就这样就ok了。

性能分析

随机序列

为了比较普通快排和随机化快排的性能，我做了一些测试。因为没有太多的经验，测试结果仅供参考。:)

数组生成代码

Random random = new Random(Calendar.getInstance().getTimeInMillis());
int[] a = new int[10000000];
int[] b = new int[10000000];
for (int i = 0; i < a.length; i++) {
    a[i] = random.nextInt(Integer.MAX_VALUE);
    b[i] = a[i];
}

测试代码：

//随机化快排
startTime = System.currentTimeMillis();
Sort.RandomQuickSort(a, 0, a.length - 1);
endTime = System.currentTimeMillis();
o(String.format("RandomQuickSort Finished. Cost %dms\n", endTime - startTime));//o是一个输出函数，把系统的System.out.print()简单封装了一下，打起来短一些……
//快排
startTime = System.currentTimeMillis();
Sort.QuickSort(b, 0, b.length - 1);
endTime = System.currentTimeMillis();
o(String.format("QuickSort Finished. Cost %dms\n", endTime - startTime));

结果：

RandomQuickSort Finished. Cost 1417ms
QuickSort Finished. Cost 1367ms

多次实验结果：

10w：

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
普通快排	13ms	15ms	15ms	14.333ms
随机化版本快排	25ms	25ms	27ms	25.667ms

100w：

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
普通快排	101ms	103ms	96ms	100ms
随机化版本快排	119ms	101ms	105ms	108.333ms

1000w：

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
普通快排	1397ms	1379ms	1338ms	1371.333ms
随机化版本快排	1241ms	1187ms	1258ms	1228.667ms

随机化快排因为要生成随机数，所以有一些性能损失，所以数据规模较小，数据分布均匀时普通快排还是比随机化快排要快些的，不过随着数据规模的上升，随机化快排的性能优势就展现出来了。

有序序列

下来才是展示快排才华的时候，假设当输入数组已经是排好序的，这两个算法的性能差距又有多少？
之前的数组生成代码不变，只是在调用两个算法之前，先调用一下快排将数组排序，然后将两个有序的数组作为参数传进去。

10w：

10w的普通快排……已经栈溢出了。

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
普通快排	溢出	溢出	溢出	溢出
随机化版本快排	15ms	7ms	6ms	9.333ms

1w：

试一试1w的

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
普通快排	98ms	94ms	92ms	94.667ms
随机化版本快排	2ms	1ms	0ms	1ms

1000w：

看下1000w下随机化快排是否有影响

算法	第1次耗时	第2次耗时	第3次耗时	平均耗时
随机化版本快排	696ms	733ms	689ms	706ms

这篇笔记就到这儿了，希望能通过讲解一遍加深记忆，也希望能给别人带来哪怕一点点帮助。

本人水平有限，如果有什么错误，请告诉我[email protected]，我会感激不尽！因为错误不仅会蒙蔽自己，也有可能会误导别人。

---

参考书籍：机械工业出版社 第三版《算法导论》部分内容引自原书