用神经网络解决拼图游戏
在一个排列不变性的数据上神经网络是困难的。拼图游戏就是这种类型的数据,那么神经网络能解决一个2x2的拼图游戏吗?
什么是置换不变性(Permutation Invariance)?
如果一个函数的输出不通过改变其输入的顺序而改变,那么这个函数就是一个排列不变量。下面是一个例子。
1) f(x,y,z) = ax + by +cz
2) f(x,y,z) = xyz
如果我们改变输入的顺序,第一个函数的输出会改变,但是第二个函数的输出不会改变。第二个函数是置换不变量。
神经网络的权值映射到特定的输入单元。当输入改变时,输出也会改变。为了学习这种对称性,权值应该是这样的即使改变了输入,最终的输出也是不变的。而前馈网络是不容易学习的。
拼图游戏也是置换不变性。不管拼图的顺序是什么,输出总是固定的。下面是一个2x2的网格难题的例子,我们将在这个项目中尝试解决它。
解决一个3x3网格的难题是极其困难的。下面是这些谜题的可能组合。
2x2 puzzle = 4! = 24 combinations
3x3 puzzle = 9! = 362880 comb’ns
为了解决一个3x3的难题,网络必须从362880中预测出一个正确的组合。这也是为什么3x3拼图是一个难题的另一个原因。
让我们继续,尝试解决一个2x2的拼图游戏。
怎么得到这些数据的?
没有任何公共数据集可用于拼图游戏,所以我必须自己创建它。我创建的数据如下。
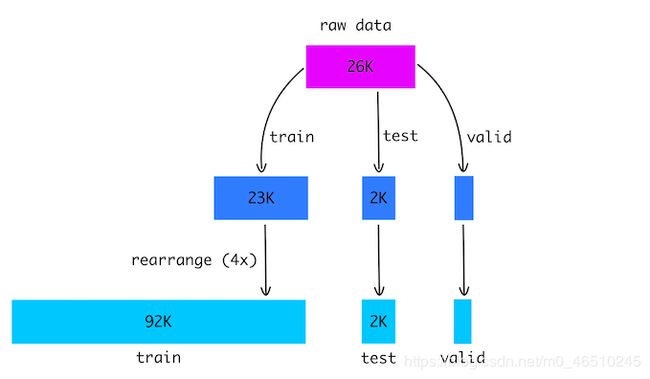
- 采集了大约26K动物图像的原始数据集。
- 裁剪所有图像到固定大小200x200。
- 将图像分割为训练、测试和验证集。
- 将图片切成4块,随机重新排列。
- 对于训练集,我重复了4次前面的步骤来增加数据。
- 最后,我们有92K个训练图像和2K个测试图像。我还分离出300张图像进行验证。
- 标签是一个整数数组,表示每个拼图块的正确位置。
这个数据集包含2x2和3x3的puzzle。你可以在这里找到它。
https://www.kaggle.com/shivajbd/jigsawpuzzle
数据是怎样的呢?
下面是一个2x2网格拼图的数据示例。输入是一个200x200像素的图像和标签是一个4个整数的数组,其中每个整数告诉每个片段的正确位置。
我们的目标是将这个图像输入到神经网络中,并得到一个输出,它是一个4个整数的向量,表示每一块的正确位置。
如何设计这个网络的?
在尝试了20多种神经网络架构和大量的尝试和错误之后,我得到了一个最优的设计。如下所示。
首先,从图像中提取每一块拼图(共4块)。
然后把每一个片段都传递给CNN。CNN提取有用的特征并输出一个特征向量。
我们使用Flatten layer将所有4个特征向量连接成一个。
然后我们通过前馈网络来传递这个组合向量。这个网络的最后一层给出了一个16单位长的向量。
我们将这个16单位向量重塑成4x4的矩阵。
为什么要做维度重塑?
在一个正常的分类任务中,神经网络会为每个类输出一个分数。我们通过应用softmax层将该分数转换为概率。概率值最高的类就是我们预测的类。这就是我们如何进行分类。
这里的情况不同。我们想把每一个片段都分类到正确的位置(0,1,2,3),这样的片段共有4个。所以我们需要4个向量(对于每个块)每个有4个分数(对于每个位置),这只是一个4x4矩阵。其中的行对应于要记分的块和列。最后,我们在这个输出矩阵行上应用一个softmax。
下面是网络图。
代码实现
我在这个项目中使用Keras框架。以下是Keras中实现的完整网络。这看起来相当简单。
model = keras.models.Sequential()
model.add(td(ZeroPadding2D(2), input_shape=(4,100,100,3))) # extra padding
model.add(td(Conv2D(50, kernel_size=(5,5), padding='same', activation='relu', strides=2))) # padding=same for more padding
model.add(td(BatchNormalization()))
model.add(td(MaxPooling2D())) # only one maxpool layerQ
model.add(td(Conv2D(100, kernel_size=(5,5), padding='same', activation='relu', strides=2)))
model.add(td(BatchNormalization()))
model.add(td(Dropout(0.3)))
model.add(td(Conv2D(100, kernel_size=(3,3), padding='same', activation='relu', strides=2)))
model.add(td(BatchNormalization()))
model.add(td(Dropout(0.3)))
model.add(td(Conv2D(200, kernel_size=(3,3), padding='same', activation='relu', strides=1)))
model.add(td(BatchNormalization()))
model.add(td(Dropout(0.3)))
model.add(Flatten()) # combining all the features
model.add(Dense(600, activation='relu'))
model.add(BatchNormalization())
model.add(Dense(400, activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.3))
model.add(Dense(16))
model.add(Reshape((4, 4))) # reshaping the final output
model.add(Activation('softmax')) # softmax would be applied row wise
模型解释
输入形状是(4,100,100,3)。我将形状(100,100,3)的4个图像(拼图)输入到网络中。
我使用的是时间分布(TD)层。TD层在输入上多次应用给定的层。在这里,TD层将对4个输入图像应用相同的卷积层(行:5,9,13,17)。
为了使用TD层,我们必须在输入中增加一个维度,TD层在该维度上多次应用给定的层。这里我们增加了一个维度,即图像的数量。因此,我们得到了4幅图像的4个特征向量。
一旦CNN特征提取完成,我们将使用Flatten层(行:21)连接所有的特征。然后通过前馈网络传递矢量。重塑最终的输出为4x4矩阵,并应用softmax(第29,30行)。
CNN的架构
这个任务与普通的分类任务完全不同。在常规的分类中,任务网络更关注图像的中心区域。但在拼图游戏中,边缘信息比中心信息重要得多。
所以我的CNN架构与平常的CNN有以下几个不同之处。
填充
我在图像通过CNN之前使用了一些额外的填充(line: 3),并且在每次卷积操作之前填充feature map (padding = same),以保护尽可能多的边缘信息。
MaxPooling
代码中尽量避免了pooling层,只使用一个MaxPool层来减小feature map的大小(行:7). pooling使得网络平移不变性,这意味着即使你旋转或晃动图像中的对象,网络仍然会检测到它。这对任何对象分类任务都很有用。
对于拼图游戏一般不希望网络具有平移不变性。我们的网络应该对变化很敏感。因为我们的边缘信息是非常敏感的。
浅层网络
我们知道CNN的顶层提取了像边缘、角等特征。当我们深入更深的层倾向于提取特征,如形状,颜色分布,等等。这和我们的案例没有太大关系,所以只创建一个浅层网络。
这些都是您需要了解CNN架构的重要细节。网络的其余部分相当简单,有3个前馈层,一个重塑层,最后一个softmax层。
训练
最后,我使用sparse_categorical_crossentropy loss和adam optimizer编译我的模型。我们的目标是一个4单位向量,告诉我们每一块的正确位置。
Target Vector: [[3],[0],[1],[2]]
我把网络训练了5个轮次。我开始时的学习率是0.001批次大小是64。在每一个轮次之后,我都在降低学习速度,增加批处理规模。
结果
在预测时,我们的网络输出一个4x4的向量,然后我们选择每行中有最大值的索引,也就是预测的位置。因此我们得到一个长度为4的向量。使用这个向量,我们还可以重新排列拼图碎片并将它们可视化。
经过训练,我在2K个未见过的批图上运行了模型,模型能够正确解决80%的谜题。
下面是由网络解决的几个样本。
作者:Shiva Verma
deephub翻译组
本文代码 https://github.com/shivaverma/Jigsaw-Solver