深度学习课程 | 《结构化机器学习项目》概念笔记—— 机器学习策略

1. 正交化方法 Orthogonalization

通过每次只调试一个参数，保持其他参数不变，而得到的模型某一个性能发生改变的一种调参策略。简单说，就是每个参数是互不影响的，是正交的。

对应到机器学习监督学习模型中，可以分成四个独立的部分，如下：

• Fit training set well on cost function

• Fit dev set well on cost function

• Fit test set well on cost function

• Performs well in real world

第一条优化训练集可以通过更大、更复杂的神经网络或者使用更好地优化算法（如Adam）来实现；
第二条优化验证集可以通过正则化或者采用更多训练样本来实现；
第三条优化测试集可以通过使用更多的验证集数据来实现；
第四条可以通过更换验证集，使用新的cost function来实现。

2. 单一数字评估指标

通过使用F1 score来评价模型的好坏，F1 score结合了precision和recall的大小，计算公式如下：
$$F1=\frac{2}{\frac{1}{R}+\frac{1}{P}}$$

除了F1 score，还可以使用平均值作为单一数字评估指标对模型进行评估。

3. 满足和优化指标

需要把所有性能指标都综合到一起，构成一个单一数字评估指标是比较困难的。为了解决这个问题，可以把某些性能作为优化指标，找到最优值；其余的性能作为满足指标，只要满足阈值即可。

4. 训练\验证\测试集的划分

合理对数据进行训练\验证\测试集的划分是非常必要的，能够提高模型训练的效率和模型的质量。

理论上，应该尽量保证验证集和测试集来源同一分布且都反映实际样本的情况。

5. 验证和测试集的大小

深度学习与机器学习的数据量不同，划分训练\验证\测试集的准则也不同。当样本（百万级别）时，划分通常遵循的比例是：98%/1%/1% 或99%/1%。

验证集数量的设置，遵循的准则是能够通过验证集检测不同算法或模型的区别，以选择出更好的模型。

测试集数量的设置，遵循的准则是通过测试集反映出模型在实际中的表现。

在实际应用中，可以只有训练集/验证-测试集，后者可以合在一起，也可以分开。

6. 贝叶斯最优误差

定义： 通过训练不断接近人类水平甚至超过它，超过它之后准确性上升比较缓慢，最终不断接近理想的最优表现。换句话说，就是理论上最小的误差。

偏差定义： 模型在训练集上的误差。——训练误差和人类水平的误差之间的差值称为偏差，也可以称为可避免偏差。
方差定义： 模型在验证集上的误差。——验证误差和训练误差之间的差值称为方差。

实际生活中，往往会使用人类水平的误差代表贝叶斯最优误差。

7. 提高你模型的表现

提高机器学习模型性能，主要是解决两个问题：可避免偏差和方差。

可避免偏差的解决方法：

1. 训练更大的模型
2. 训练使用更好、更大的优化算法：momentum, RMSprop, Adam
3. 修改卷积网络结构和超参数搜索

方差的解决方法：

1. 提供更多的数据
2. 正则化：L2，dropout，数据增强
3. 修改卷积网络结构和超参数搜索

8. 误差分析

错误分析主要是对结果影响较大的因素进行改进。

统计数据集中所有预测错误的样本所占的比例，如果某些负样本所占的比重比较小（5%左右），那么就没有很大的必要对样本进行处理；若比重比较大（50%以上），改进模型能够改善性能，就值得花时间去对样本进行分析。

错误分析可以同时评估几个影响模型性能的因素（如，修正被某些非正样本的目标被预测错误；改善模糊图像的性能；进行图像增强等），通过各自在错误样本中所占的比例来判断其重要性。

9. 清楚标注错误的数据

监督学习中，可能会出现标签y被标注错误的情况。

无论是训练集、验证集、测试集都可能会出现标签y被标注错误的情况，使用8中的错误分析统计出所有预测错误的样本中错误标签数据所占的比例，根据比例大小从而决定是否要修正被错误标注的数据。

对于修正标注错误的验证集和测试集，有几点注意事项：

• 确保你的验证集和测试集均来自同一分布；
• 考虑一下你的算法正确与错误的例子；
• 训练和验证/测试数据可能来自不同的分布。

10. 当数据来自不同分布时，如何划分训练、验证和测试集

有两种方法：

• 第一种做法是将训练集和验证/测试集完全混合起来，然后随机选择一部分作为训练集，另一部分作为验证/测试集。——优点：训练集和验证/测试集的分布一致。缺点：来自分布较差的样本在验证集上占比例可能会大。

• 第二种做法是将原来的训练集和一部分验证/测试集组合当成“训练集”，剩下的验证/测试集分别作为验证集和测试集。

11. 不匹配数据划分的偏差和方差

在分布不同的数据集（训练、验证、测试）下，不能直接通过相对值大小来判断是否有偏差和方差。

Andrew给出一个方法，定义一个train-dev set，用这个数据集来验证方差。具体做法是：从原来的训练集中分出一部分作为train-dev set，这部分并不参与训练，与验证集一样用于验证。

现在就有三种误差，分别是训练误差、训练-验证误差、验证误差。训练误差和训练-验证误差的差值反映的是方差（variance)，训练-验证误差和验证误差的差值反映的是样本分布不一致（mismatch problem）。

误差的差值以及所反映的问题，可以用如下图表示：

12. 迁移学习(Transfer learning)

定义： 将已经训练好的模型直接应用到另一个类似的模型中去，无需重新构建新的模型，而是利用之前的神经网络模型，只改变样本输入、输出和输出层的权重系数，不改变其他层所有的权重系数。

如果数据样本比较多，可以只保留网络结构，重新训练所有层的权重系数。根据具体数据量大小，选择不同的方法。

预训练：重新训练所有权重系数，但初始权重系数是由之前的模型训练得到的。

微调（fine-tuning）：通过调参等操作不断优化$W^{[l]}$和$b^{[l]}$。

在计算机视觉方面，就经常使用这样的学习方法。

（图片来源）

迁移学习应用的三种场合：

1. 任务A和任务B输入相同；
2. 与任务B相比，任务A的数据要多很多；
3. 任务A的低级功能可能有助于学习任务B。

13. 多任务学习

定义： 构建单个神经网络同时执行多个任务，类似于将多个神经网络融合在一起，用一个网络模型来实现多种不同的效果。实际应用中，也可以分别构建多个神经网络来实现多个任务。

多任务学习应用的三种场合：

1. 训练任务时，这些任务可以共用低层次特征；
2. 每个任务的数据量很接近；
3. 当训练足够大的神经网络时，同时做好所有的工作。

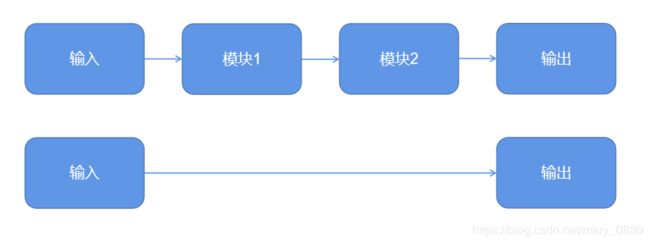
14. 端到端学习（end-to-end learning）

定义：将所有不同阶段的数据处理系统或学习系统模块组合在一起，用一个单一的神经网络模型来实现所有的功能，即将所有的模块合在一起，只有输入和输出。

当训练样本足够多，神经网络模型足够复杂，则端到端学习模型比传统机器学习模型更好。

优点：

1. 仅使用一个模型、一个目标函数，比较简单；
2. 减少所需模型的手工设计，减少工程的复杂度。

缺点：

1. 需要大量的数据。
2. 排除可能有用的手工设计。