十三、数字图像处理之小波基础
小波
- （一）小波概念
- （二）快速小波变换FWT
- （1）使用小波工具箱的FWT
- （2）不使用小波工具箱的FWT
- （三）快速小波反变换
- （四）小波分解结构的处理
- （1）不使用小波工具箱编辑小波分解系数
- （2）显示小波分解系数
- （五）图像中的小波运用
（一）小波概念
小波变换（wavelet transform，WT）是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，能对时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了 Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。（来自百度百科）
通俗来说， 小波，一个神奇的波，可长可短可胖可瘦，如图所示：
（a）是我们熟悉的傅里叶变换正弦波；（b）DWT展开函数是持续时间受限且频率不断变化的“小波”
小波的一般特性：
- 可分离性、可伸缩性和平移性；
- 多分辨率的兼容性；
- 正交性。
（二）快速小波变换FWT
概念：快速小波变换，也叫快速小波转换（英语：Fast wavelet transform）是利用数学的演算法则用来转换在时域的波形或信号变成一系列的以正交基底构成的小而有限的小波。 当然，快速小波转换本身可以很轻易地扩增它的维度以符合各种不同的需求，例如影像处理、压缩、去除噪声。（来自百度百科）
FWT滤波器计算原理如下：
其中，“实星号”表示卷积，在非负处计算卷积值，偶数指针等价于滤波和由2下取样。
下面有两种方法来处理快速小波变换，分别是：使用小波工具箱的FWT（函数wfilters和函数wavedec2）、不使用小波工具箱的FWT（函数waverec2和函数waveback）。
（1）使用小波工具箱的FWT
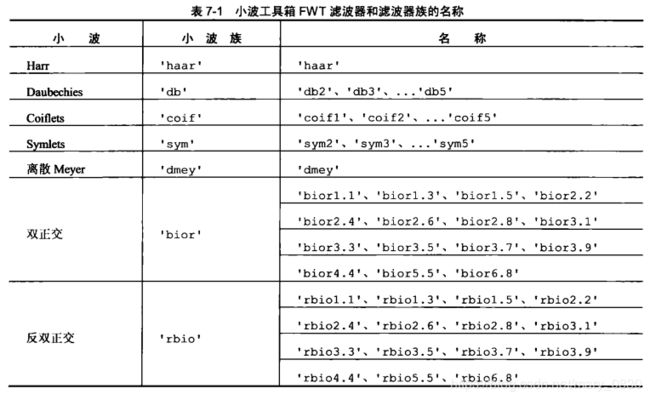
- 小波工具箱为各种快速小波变换提供分解滤波器，与特殊变换有关的滤波器可通过函数wfilters来访问，基本语法为：
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wname);
其中，wname是滤波器名称，Lo_D,Hi_D,Lo_R,Hi_R这四个参数是行向量，分别返回低通分解、高通分解、低通重建和高通重建滤波器。
- 频率耦合滤波器可以用下面语法处理：
[F1,F2] = wfilters(wname,type)
- 为了在命令窗口中打印小波族wfamily的描述信息，在提示符后键入：
waveinfo(wfamily)
- 为了获得归一化正交变换的尺度和小波函数的数字近似值，可键入：
[phi,psi,xval] = wavefun(wname,iter)
- 双正交变换，可键入：
[phi1,psi1,phi2,psi2,xval] = wavefun(wname,iter)
其中，phi1,psi1是分解函数，phi2,psi2是重建函数。
实验代码：
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('haar')
得到结果：
waveinfo('haar') %获得小波族的描述信息
[phi,psi,xval] = wavefun('haar',10); %归一化正交变换的haar小波和小波函数的数字近似值为10
xaxis = zeros(size(xval));
subplot(121);
plot(xval,phi,'k',xval,xaxis,'--k');
axis([0 1 -1.5 1.5]);
axis square;
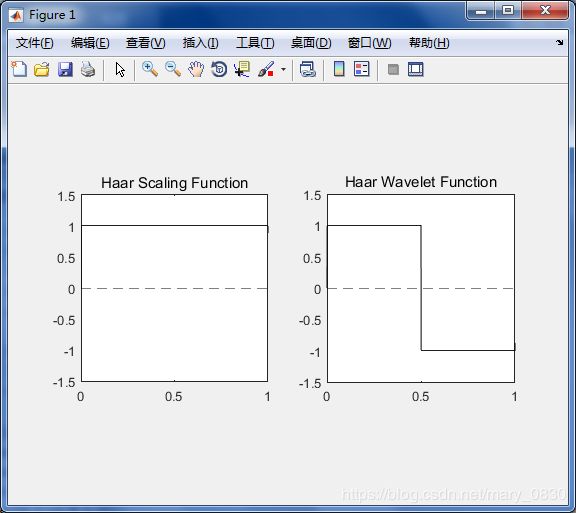
title('Haar Scaling Function'); %haar尺度函数
subplot(122);
plot(xval,psi,'k',xval,xaxis,'--k');
axis([0 1 -1.5 1.5]);
axis square;
title('Haar Wavelet Function'); %haar小波函数
计算小波变换是用函数wavedec2处理的，基本语法是：
[C,S] = wavedec2(X,N,Lo_D,Hi_D) %Lo_D,Hi_D是一组分解滤波器，X是二维图形或矩阵，N是被计算的尺度数
也可以用下面修改的语法来处理：
[C,S] = wavedec2(x,n,wname) %wname是上面图表的小波滤波器
用以上函数编写实验代码：
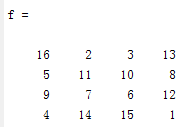
f = magic(4)
[c1,s1] = wavedec2(f,1,'haar')
[c2,s2] = wavedec2(f,2,'haar')
（2）不使用小波工具箱的FWT
当我们不使用小波工具箱时，可以用函数wavefilter和wavefast来处理小波的分解和重建。
- 函数wavefilter：小波分解和重构的滤波器
function [varargout] = wavefilter(wname, type)
error(nargchk(1, 2, nargin));
if (nargin == 1 & nargout ~= 4) | (nargin == 2 & nargout ~= 2)
error('Invalid number of output arguments.');
end
if nargin == 1 & ~ischar(wname)
error('WNAME must be a string.');
end
if nargin == 2 & ~ischar(type)
error('TYPE must be a string.');
end
% Create filters for the requested wavelet.
switch lower(wname)
case {'haar', 'db1'}
ld = [1 1]/sqrt(2); hd = [-1 1]/sqrt(2);
lr = ld; hr = -hd;
case 'db4'
ld = [-1.059740178499728e-002 3.288301166698295e-002 ...
3.084138183598697e-002 -1.870348117188811e-001 ...
-2.798376941698385e-002 6.308807679295904e-001 ...
7.148465705525415e-001 2.303778133088552e-001];
t = (0:7);
hd = ld; hd(end:-1:1) = cos(pi * t) .* ld;
lr = ld; lr(end:-1:1) = ld;
hr = cos(pi * t) .* ld;
case 'sym4'
ld = [-7.576571478927333e-002 -2.963552764599851e-002 ...
4.976186676320155e-001 8.037387518059161e-001 ...
2.978577956052774e-001 -9.921954357684722e-002 ...
-1.260396726203783e-002 3.222310060404270e-002];
t = (0:7);
hd = ld; hd(end:-1:1) = cos(pi * t) .* ld;
lr = ld; lr(end:-1:1) = ld;
hr = cos(pi * t) .* ld;
case 'bior6.8'
ld = [0 1.908831736481291e-003 -1.914286129088767e-003 ...
-1.699063986760234e-002 1.193456527972926e-002 ...
4.973290349094079e-002 -7.726317316720414e-002 ...
-9.405920349573646e-002 4.207962846098268e-001 ...
8.259229974584023e-001 4.207962846098268e-001 ...
-9.405920349573646e-002 -7.726317316720414e-002 ...
4.973290349094079e-002 1.193456527972926e-002 ...
-1.699063986760234e-002 -1.914286129088767e-003 ...
1.908831736481291e-003];
hd = [0 0 0 1.442628250562444e-002 -1.446750489679015e-002 ...
-7.872200106262882e-002 4.036797903033992e-002 ...
4.178491091502746e-001 -7.589077294536542e-001 ...
4.178491091502746e-001 4.036797903033992e-002 ...
-7.872200106262882e-002 -1.446750489679015e-002 ...
1.442628250562444e-002 0 0 0 0];
t = (0:17);
lr = cos(pi * (t + 1)) .* hd;
hr = cos(pi * t) .* ld;
case 'jpeg9.7'
ld = [0 0.02674875741080976 -0.01686411844287495 ...
-0.07822326652898785 0.2668641184428723 ...
0.6029490182363579 0.2668641184428723 ...
-0.07822326652898785 -0.01686411844287495 ...
0.02674875741080976];
hd = [0 -0.09127176311424948 0.05754352622849957 ...
0.5912717631142470 -1.115087052456994 ...
0.5912717631142470 0.05754352622849957 ...
-0.09127176311424948 0 0];
t = (0:9);
lr = cos(pi * (t + 1)) .* hd;
hr = cos(pi * t) .* ld;
otherwise
error('Unrecognizable wavelet name (WNAME).');
end
% Output the requested filters.
if (nargin == 1)
varargout(1:4) = {ld, hd, lr, hr};
else
switch lower(type(1))
case 'd'
varargout = {ld, hd};
case 'r'
varargout = {lr, hr};
otherwise
error('Unrecognizable filter TYPE.');
end
end
- 函数wavefast：用来处理对称图像扩展，减少因计算FWT而产生边缘失真
function [c, s] = wavefast(x, n, varargin)
error(nargchk(3, 4, nargin));
if nargin == 3
if ischar(varargin{1})
[lp, hp] = wavefilter(varargin{1}, 'd');
else
error('Missing wavelet name.');
end
else
lp = varargin{1}; hp = varargin{2};
end
fl = length(lp); sx = size(x);
if (ndims(x) ~= 2) | (min(sx) < 2) | ~isreal(x) | ~isnumeric(x)
error('X must be a real, numeric matrix.');
end
if (ndims(lp) ~= 2) | ~isreal(lp) | ~isnumeric(lp) ...
| (ndims(hp) ~= 2) | ~isreal(hp) | ~isnumeric(hp) ...
| (fl ~= length(hp)) | rem(fl, 2) ~= 0
error(['LP and HP must be even and equal length real, ' ...
'numeric filter vectors.']);
end
if ~isreal(n) | ~isnumeric(n) | (n < 1) | (n > log2(max(sx)))
error(['N must be a real scalar between 1 and ' ...
'log2(max(size((X))).']);
end
% Init the starting output data structures and initial approximation.
c = []; s = sx; app = double(x);
% For each decomposition ...
for i = 1:n
% Extend the approximation symmetrically.
[app, keep] = symextend(app, fl);
% Convolve rows with HP and downsample. Then convolve columns
% with HP and LP to get the diagonal and vertical coefficients.
rows = symconv(app, hp, 'row', fl, keep);
coefs = symconv(rows, hp, 'col', fl, keep);
c = [coefs(:)' c]; s = [size(coefs); s];
coefs = symconv(rows, lp, 'col', fl, keep);
c = [coefs(:)' c];
% Convolve rows with LP and downsample. Then convolve columns
% with HP and LP to get the horizontal and next approximation
% coeffcients.
rows = symconv(app, lp, 'row', fl, keep);
coefs = symconv(rows, hp, 'col', fl, keep);
c = [coefs(:)' c];
app = symconv(rows, lp, 'col', fl, keep);
end
% Append final approximation structures.
c = [app(:)' c]; s = [size(app); s];
%-------------------------------------------------------------------%
function [y, keep] = symextend(x, fl)
% Compute the number of coefficients to keep after convolution
% and downsampling. Then extend x in both dimensions.
keep = floor((fl + size(x) - 1) / 2);
y = padarray(x, [(fl - 1) (fl - 1)], 'symmetric', 'both');
%-------------------------------------------------------------------%
function y = symconv(x, h, type, fl, keep)
% Convolve the rows or columns of x with h, downsample,
% and extract the center section since symmetrically extended.
if strcmp(type, 'row')
y = conv2(x, h);
y = y(:, 1:2:end);
y = y(:, fl / 2 + 1:fl / 2 + keep(2));
else
y = conv2(x, h');
y = y(1:2:end, :);
y = y(fl / 2 + 1:fl / 2 + keep(1), :);
end
- 函数fwtcompare：用于比较wavefast和wacedec2的执行时间
function [ratio, maxdiff] = fwtcompare(f, n, wname)
% Get transform and computation time for wavedec2.
tic;
[c1, s1] = wavedec2(f, n, wname);
reftime = toc;
% Get transform and computation time for wavefast.
tic;
[c2, s2] = wavefast(f, n, wname);
t2 = toc;
% Compare the results.
ratio = t2 / (reftime + eps);
maxdiff = abs(max(c1 - c2));
编写代码如下：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0619(a).tif');
[ratio,maxdifference] = fwtcompare(f,5,'db4')
（三）快速小波反变换
下图是快速小波变换的逆过程：
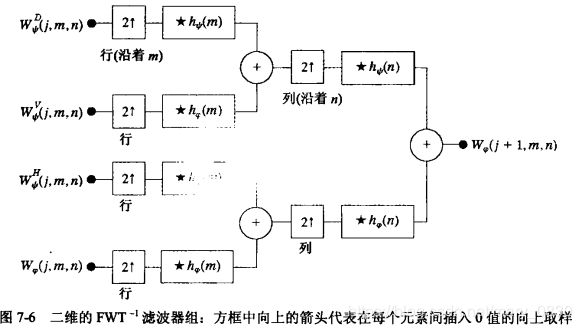
其中，“实星号”表示卷积，在非负处计算卷积值，偶数指针等价于滤波和由2上取样。
- 当使用小波工具箱内的函数waverec2用来计算小波分解结构[C,S] 的反快速小波变换：
g = waverec2(C,S,wname)； %g是得到重构后的二维图像
g = waverec2(C,S,LO_R,HI_R); %要求的重构图像可以通过下面语句实现
- 当不使用小波工具箱时，可以调用函数waveback处理小波重构。
function [varargout] = waveback(c, s, varargin)
% Check the input and output arguments for reasonableness.
error(nargchk(3, 5, nargin));
error(nargchk(1, 2, nargout));
if (ndims(c) ~= 2) | (size(c, 1) ~= 1)
error('C must be a row vector.');
end
if (ndims(s) ~= 2) | ~isreal(s) | ~isnumeric(s) | (size(s,2) ~= 2)
error('S must be a real, numeric two-column array.');
end
elements = prod(s, 2);
if (length(c) < elements(end)) | ...
~(elements(1) + 3 * sum(elements(2:end - 1)) >= elements(end))
error(['[C S] must be a standard wavelet ' ...
'decomposition structure.']);
end
% Maximum levels in [C, S].
nmax = size(s, 1) - 2;
% Get third input parameter and init check flags.
wname = varargin{1}; filterchk = 0; nchk = 0;
switch nargin
case 3
if ischar(wname)
[lp, hp] = wavefilter(wname, 'r'); n = nmax;
else
error('Undefined filter.');
end
if nargout ~= 1
error('Wrong number of output arguments.');
end
case 4
if ischar(wname)
[lp, hp] = wavefilter(wname, 'r');
n = varargin{2}; nchk = 1;
else
lp = varargin{1}; hp = varargin{2};
filterchk = 1; n = nmax;
if nargout ~= 1
error('Wrong number of output arguments.');
end
end
case 5
lp = varargin{1}; hp = varargin{2}; filterchk = 1;
n = varargin{3}; nchk = 1;
otherwise
error('Improper number of input arguments.');
end
fl = length(lp);
if filterchk % Check filters.
if (ndims(lp) ~= 2) | ~isreal(lp) | ~isnumeric(lp) ...
| (ndims(hp) ~= 2) | ~isreal(hp) | ~isnumeric(hp) ...
| (fl ~= length(hp)) | rem(fl, 2) ~= 0
error(['LP and HP must be even and equal length real, ' ...
'numeric filter vectors.']);
end
end
if nchk & (~isnumeric(n) | ~isreal(n)) % Check scale N.
error('N must be a real numeric.');
end
if (n > nmax) | (n < 1)
error('Invalid number (N) of reconstructions requested.');
end
if (n ~= nmax) & (nargout ~= 2)
error('Not enough output arguments.');
end
nc = c; ns = s; nnmax = nmax; % Init decomposition.
for i = 1:n
% Compute a new approximation.
a = symconvup(wavecopy('a', nc, ns), lp, lp, fl, ns(3, :)) + ...
symconvup(wavecopy('h', nc, ns, nnmax), ...
hp, lp, fl, ns(3, :)) + ...
symconvup(wavecopy('v', nc, ns, nnmax), ...
lp, hp, fl, ns(3, :)) + ...
symconvup(wavecopy('d', nc, ns, nnmax), ...
hp, hp, fl, ns(3, :));
% Update decomposition.
nc = nc(4 * prod(ns(1, :)) + 1:end); nc = [a(:)' nc];
ns = ns(3:end, :); ns = [ns(1, :); ns];
nnmax = size(ns, 1) - 2;
end
if nargout == 1
a = nc; nc = repmat(0, ns(1, :)); nc(:) = a;
end
varargout{1} = nc;
if nargout == 2
varargout{2} = ns;
end
%-------------------------------------------------------------------%
function z = symconvup(x, f1, f2, fln, keep)
y = zeros([2 1] .* size(x)); y(1:2:end, :) = x;
y = conv2(y, f1');
z = zeros([1 2] .* size(y)); z(:, 1:2:end) = y;
z = conv2(z, f2);
z = z(fln - 1:fln + keep(1) - 2, fln - 1:fln + keep(2) - 2);
- 函数ifwtcompare：用于比较waveback和wacerec2的执行时间
function [ratio, maxdiff] = ifwtcompare(f, n, wname)
% Compute the transform and get output and computation time for
% waverec2.
[c1, s1] = wavedec2(f, n, wname);
tic;
g1 = waverec2(c1, s1, wname);
reftime = toc;
% Compute the transform and get output and computation time for
% waveback.
[c2, s2] = wavefast(f, n, wname);
tic;
g2 = waveback(c2, s2, wname);
t2 = toc;
% Compare the results.
ratio = t2 / (reftime + eps);
maxdiff = abs(max(max(g1 - g2)));
和正变换一样，用小波对图像进行5级变换，编写代码：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0619(a).tif');
[ratio,maxdifference] = ifwtcompare(f,5,'db4')
解释：两个函数的逆变换次数是相似的（比率仅为0.5026），并且最大输出差别仅为3.9790e-13。在实际用途中，本质上差别不大。因此，当有没有小波工具箱的帮助时，执行时间基本上没有差别，用哪种函数都可以用小波来重构图像。同理，函数wavedec2和函数wavefast的执行时间也是相差不大。但是有一点需要注意的是，当产生实质上相同的结果时，函数wavefast比小波工具箱提供的函数wavedec2要快一些。
（四）小波分解结构的处理
实验代码：
f = magic(8);
[c1,s1] = wavedec2(f,3,'haar');
size(c1)
s1
approx = appcoef2(c1,s1,'haar') %提取小波
horizdet2 = detcoef2('h',c1,s1,2) %级别2的水平细节系数
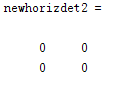
newc1 = wthcoef2('h',c1,s1,2) %设置小波阈值函数
newhorizdet2 = detcoef2('h',newc1,s1,2)
实验结果：
（1）不使用小波工具箱编辑小波分解系数
说明： 不使用小波工具箱，记录矩阵S是单独访问多尺度向量c的近似和细节系数的关键。
函数wavework是以剪切-复制-粘贴为基础处理小波的方法。分别产生了函数wavecut、函数wavecopy、函数wavepaste，这样更好的处理向量c。
实验代码：
f = magic(8);
[c1,s1] = wavedec2(f,3,'haar');
approx = wavecopy('a',c1,s1)
horizdet2 = wavecopy('h',c1,s1,2)
[newc1,horizdet2] = wavecut('h',c1,s1,2);
newhorizdet2 = wavecopy('h',newc1,s1,2)
实验结果：
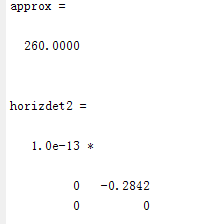
实验分析：本次得到的结果和上面实验获得结果一致，其提取的所有矩阵一致。其原因是函数wavecut和函数wavecopy可以用上面实验结果重新产生小波工具箱，这个作用就相当于常在word中剪切-复制-粘贴一样，这是小波中的剪切-复制-粘贴。即使没有使用小波工具箱，依然可以通过这三步骤获得小波工具箱中的函数来处理小波分解。
（2）显示小波分解系数
这里说明用函数wavedisplay执行子图像合成，标定这些系数以便更好地显示它们之间的区别，并且插入描绘近似和各个水平、垂直及对角线细节矩阵的边界。
实验代码：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0704.tif');
[c,s] = wavefast(f,2,'db4'); %尺度为2的小波变换
subplot(131),wave2gray(c,s); %按照自动比例放大
subplot(132),wave2gray(c,s,8); %按照8倍比例放大
subplot(133),wave2gray(c,s,-8); %按照绝对值8倍比例放大
实验结果：
实验分析： 对比同一图像的三幅图，第一幅基本看不出细节系数是由于没有附加上比例缩放系数，第二、第三幅就显示了图像细节；第二幅图是被放大8倍以后得到的细节描述，它和第三幅图不一样的地方在于，是以中等灰度填充的，并不是黑色。第三幅图显示填充为黑色，是由于细节系数取绝对值后的结果。如果输入scale是正数，那么细节系数是以中等灰度显示，若输入scale是负数，则细节系数的绝对值将以黑色填充。这次运用的小波变换是Daubechies（小波基）中的’db4’，这个小波滤波器是可以变换的，当实验换成’haar’，那么效果会如何？
修改代码并显示如下：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0704.tif');
[c,s] = wavefast(f,2,'haar'); %尺度为2的小波变换
subplot(131),wave2gray(c,s); %按照自动比例放大
subplot(132),wave2gray(c,s,8); %按照8倍比例放大
subplot(133),wave2gray(c,s,-8); %按照绝对值8倍比例放大
对于花瓶图像，小波滤波器换成’haar’比’db4’显示出来的细节更加多一些，这是由于不同滤波器的效果是会出现差别的，当需要满足不同的需求时，可以使用不同的滤波器来处理不同的情况。
（五）图像中的小波运用
基于小波处理的基本过程就是：
- 计算一幅图像的二维小波变换
- 修改变换系数
- 计算反变换
实验一代码：小波定向和边缘检测
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0513(a).tif');
subplot(221),imshow(f),title('原始图像');
[c,s] = wavefast(f,1,'sym4');
subplot(222);wavedisplay(c,s,-6),title('小波变换后的图像');
[nc,y] = wavecut('a',c,s);
subplot(223);wavedisplay(nc,s,-6),title('将所有近似系数设为0的图像');
edges = abs(waveback(nc,s,'sym4'));
subplot(224),imshow(mat2gray(edges)),title('计算反变换的绝对值从而得到边缘图像');
实验一结果：
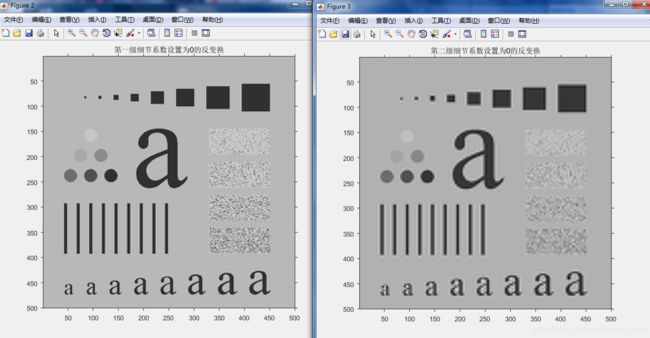
实验二代码：基于小波的图像平滑及模糊
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0513(a).tif');
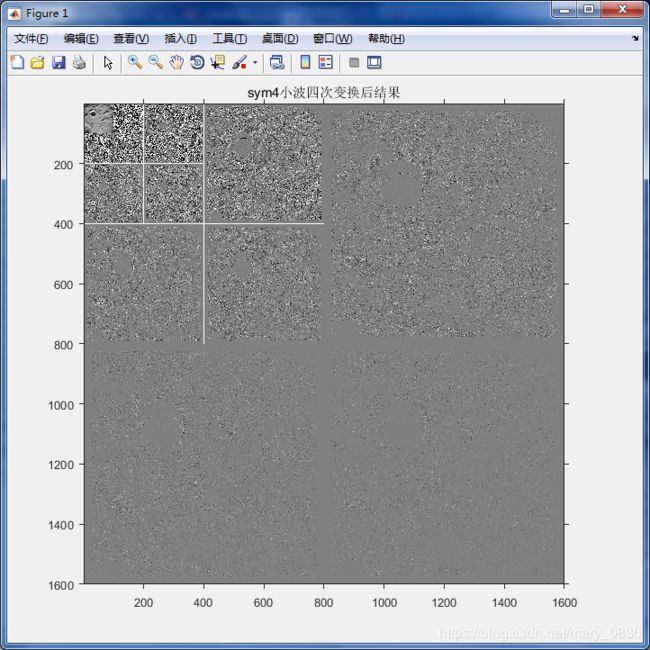
[c,s] = wavefast(f,4,'sym4'); %小波变换后图像
wavedisplay(c,s,20),title('sym4小波四次变换后结果');
[c,g8] = wavezero(c,s,1,'sym4'),title('第一级细节系数设置为0的反变换');
[c,g8] = wavezero(c,s,2,'sym4'),title('第二级细节系数设置为0的反变换');
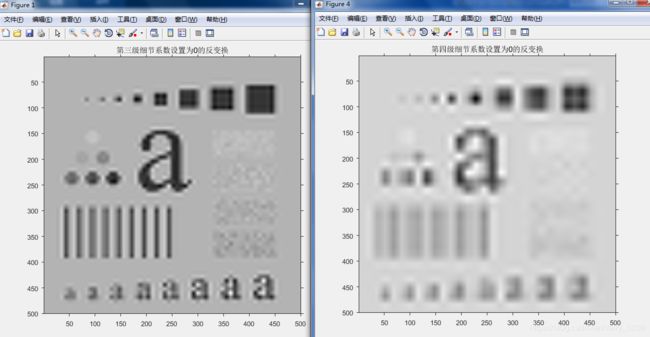
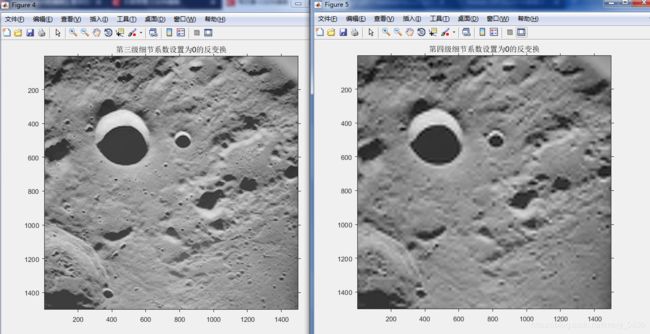
[c,g8] = wavezero(c,s,3,'sym4'),title('第三级细节系数设置为0的反变换');
[c,g8] = wavezero(c,s,4,'sym4'),title('第四级细节系数设置为0的反变换');
实验二结果：
实验三代码：渐进重构
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0219(a).tif');
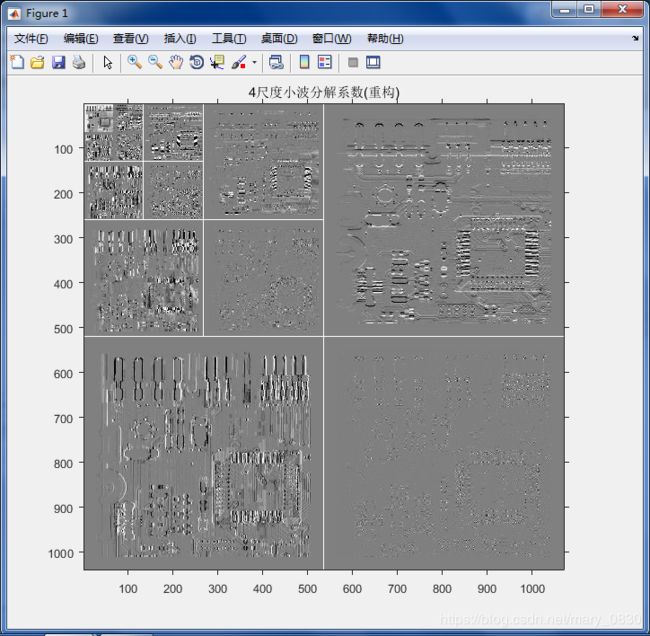
[c,s] = wavefast(f,4,'jpeg9.7');
wavedisplay(c,s,8),title('4尺度小波分解系数(重构)');
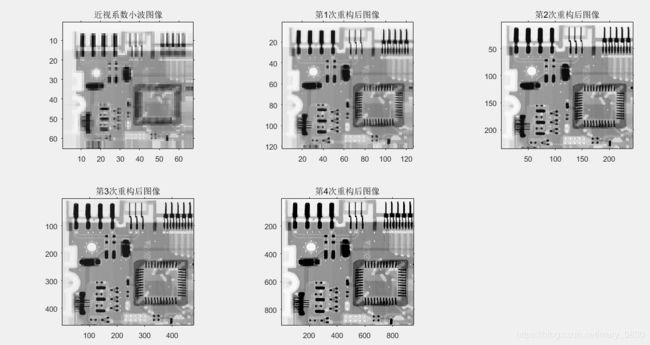
f =wavecopy('a',c,s);
subplot(231),imshow(mat2gray(f)),title('近视系数小波图像');;
[c,s] = waveback(c,s,'jpeg9.7',1);
f =wavecopy('a',c,s);
subplot(232),imshow(mat2gray(f)),title('第1次重构后图像');
[c,s] = waveback(c,s,'jpeg9.7',1);
f =wavecopy('a',c,s);
subplot(233),imshow(mat2gray(f)),title('第2次重构后图像');
[c,s] = waveback(c,s,'jpeg9.7',1);
f =wavecopy('a',c,s);
subplot(234),imshow(mat2gray(f)),title('第3次重构后图像');
[c,s] = waveback(c,s,'jpeg9.7',1);
f =wavecopy('a',c,s);
subplot(235),imshow(mat2gray(f)),title('第4次重构后图像');
实验三结果：
实验总结：
小波变换和傅里叶变换一样都可以用于边缘检测、图像平滑、图像重建。但小波变换比傅里叶变换更好之处在于，它可以用于时域频域局部同时分析。傅里叶变换和小波变换的区别是：傅立叶变换分析中，以单个变量（时间或频率）的函数表示信号，所以不能同时作时域频域分析。小波变换分析中，利用联合时间——尺度函数分析信号，通过平移和伸缩构造小波基，由于小波同时具有时间平移和多尺度分辨率的特点，可以同时进行时频域分析。小波还可以解决傅里叶变换处理不了的非稳定信号，因此小波也常用于图像处理。