GNN Pooling(三)：An End-to-End Deep Learning Architecture for Graph Classification，AAAI2018；以及图核

本文的作者来自Department of Computer Science and Engineering, Washington University in St. Louis。
本文提出了一种接受任意结构图的新型神经网络结构，主要解决了图分类问题中的两个挑战：1)如何提取有用的特征来描述编码在图中的丰富信息，以达到分类的目的;2)如何以有意义和一致的顺序读取图。从实际的操作来看，这两个challenge分别对应图卷积以及图池化。对此，本文设计了一个局部图卷积模型，并给出了它与两个图核的关系；设计了一个新的排序池层，以一致的顺序对图顶点进行排序，这样传统的神经网络就可以在图上进行训练；并通过top-k选取对卷积之后的图进行池化。
本文的贡献如下：
1)我们提出了一种新颖的端到端深度学习结构用于图分类。它直接接受图形作为输入，不需要任何预处理。
2)提出了一种新的空间图卷积层来提取多尺度的顶点特征，并与目前流行的图核进行了类比来解释其工作原理。
3)我们开发了一个新的排序池层来对顶点特征进行排序，而不是对它们进行汇总，这样可以保留更多的信息，并允许我们从全局图的拓扑结构中学习。
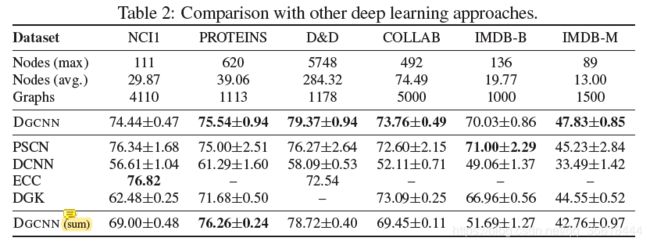
4)在基准图分类数据集上的实验结果表明，我们的深度图卷积神经网络(DGCNN)与先进的图核具有很强的竞争力，并且在图分类方面明显优于许多其他深度学习方法。
由于本文在模型描述中对比了图核，因此最开始咱们先看看图核到底是个啥。

核，图核，图卷积核

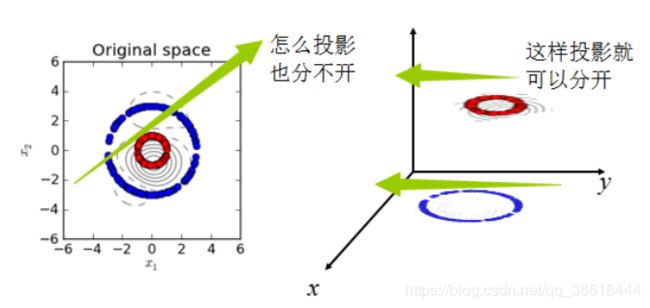
首先，我们先复习一下机器学习里常见的核函数。核函数可以理解为一种变换，以SVM中常提到的核函数举例，SVM通过超平面将数据分类，而对于一些不可分的数据，通过核函数将其变换到另一个空间，再进行分类（图片来源）。

图核（Graph Kernal）从名字上来说，应该可以理解为“对图上的特征的一种变换方式”，我在必应学术上找到了图核对应的标签定义：
a graph kernel is a kernel function that computes an inner product on graphs。Graph kernels can be intuitively understood as functions measuring the similarity of pairs of graphs. They allow kernelized learning algorithms such as support vector machines to work directly on graphs, without having to do feature extraction to transform them to fixed-length, real-valued feature vectors。
大概就是说，图核是在图上计算內积的核函数，直观上可以理解为两个图相似度的衡量方式。图核允许核化学习算法(如支持向量机)直接在图上工作，而不需要进行特征提取来将它们转换为固定长度的实值特征向量。
看到这里我想到GNN中的卷积核，也是图核的一种。中科院沈华伟老师把Kernel function描述为：Characterizing the similarity or distance among nodes，其本质也与图核一致。顺便一提，我们都知道图卷积分为两种：Spectral methods和Spatial Methods。现在的研究达成共识，谱方法就是空间方法的特例，而二者在实际操作中的不同则被归纳为：空间方法需要直接定义核函数，而谱方法不必。而对于谱方法，也可以在推导的时候看到卷积核：

图中给出了三种不同的GNN，以最原始的谱方法为例，核参数为θ，卷积核为uu^T。而GCN则要简单很多了，（I-L） 为核。
不过，在我看来，核也决定了特征聚合的方式，因此为了方便理解，核被看做是一系列操作，这个操作规定了如何从邻居结点聚合特征。这个在接下来的论文里真正介绍图核的实际例子的时候可以看到。

Deep Graph Convolutional Neural Network (DGCNN)

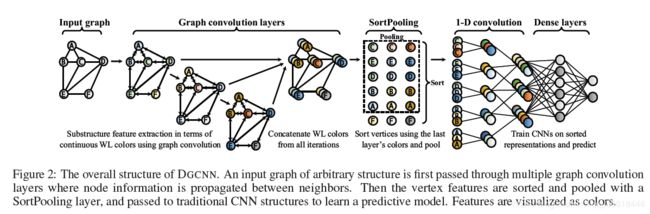
本文首先提出了一个图卷积网络GDCNN。这个东西有三个不同步骤：1)图卷积层提取顶点的局部子结构特征，定义一致的顶点排序;2)排序池层按照前面定义的顺序对顶点特征进行排序，并统一输入大小;3)传统的卷积稠密层读取已排序图表示并进行预测。
一些符号，都是GCN里常见的：X∈R^n×c,X是特征矩阵，n是图中结点数，c是特征维度。参考CNN中的定义，可以把c理解为通道数（channel）。A当然是邻接矩阵咯，没有闭环的那种。然后又定义了Pi作为任何矩阵P的i^th行。结点v的邻居使用Γ(v)来表示。

Graph convolution layers

本文中的图卷积为：

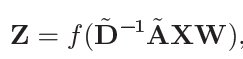
A_hat = A + I，D_hat通过如下方式计算：

W∈R^c×c’,Z∈R^n×c’，这都是Kipf论文里提到过的。当然，和原论文里的公式还是稍有不同：

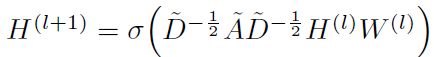
本文的方法为了和图核进行一个关系的比较，因此需要再进一步推导。假定Y := XW，就有如下表示形式：

这个公式的解释为：i^th结点的行可以表示为结点Yi自身以及邻居Yj的和，本质上依旧是GCN的特征聚合思想。然后，为了提取更深层次的特征，把许多上述卷积操作堆叠起来，就构成了一个深度网络：

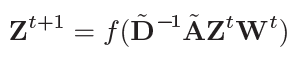
最终，把所有的Z^t t=1,2,3…h堆叠起来，得到Z^1:h:=[Z¹…Z^h]，这个东西就是卷积层的输出。接下来就是把本文的卷积方式（可以理解为图核）与其他图核进行对比。

Connection with Weisfeiler-Lehman subtree kernel

我会按照论文里提到的简单介绍一下这个图核，若是以后有时间且有兴趣，我会单独读一系列有关图核的论文（flag立下了不知道会不会有后续啊哈哈）。
Weisfeiler-Lehman subtree kernel（WL）基本思想是将顶点的颜色与其1跳邻居的颜色连接起来作为顶点的WL签名，然后按字典顺序对签名字符串进行排序，以分配新的颜色；具有相同签名的顶点被赋予相同的新颜色。重复这个过程，直到颜色收敛或达到某个最大迭代h，这些具有相同颜色的结点就代表同一含义。如果两个图是同构的，他们将在尽可能多的点集上拥有相同的颜色。
举一个实际的例子，abcde按照顺序给出了WL的计算步骤。首先，每一个结点获取邻居结点的信息构成一个新的点集。然后每个不同的点集都被映射成新的结点id（signature），并分配不同的颜色。比如，图c中的1,4→6。如此一来带有全新签名的图就形成了，每个签名实际上浓缩了图的拓扑结构信息。然后，用颜色以及签名就可以获取到图的表示。图d中，每一位表示一个颜色，数字注意表示签名出现的次数。这样就可以通过比较两个特征向量之间的相似性决定两个图的相似程度了。

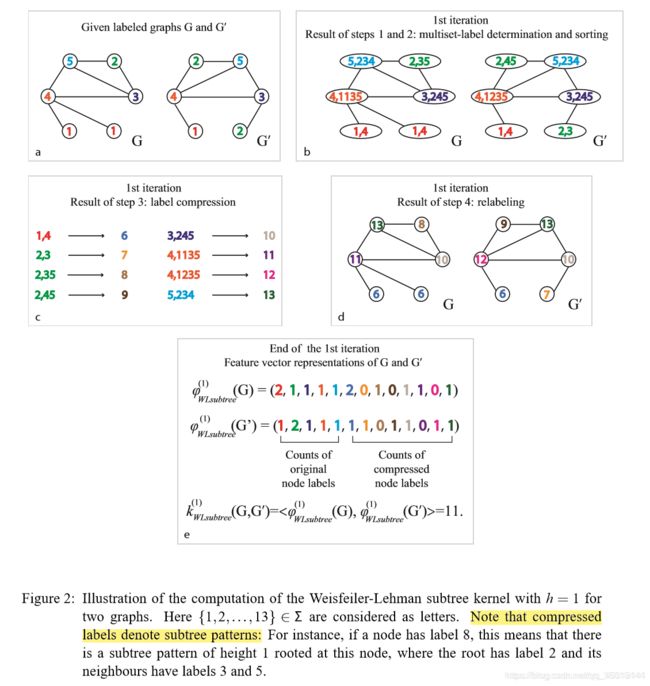
俩特征向量的相似程度有一个单独的公式：

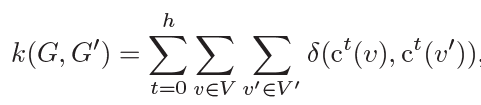
c^t(v)表示结点v在第t次迭代的颜色，遍历每次迭代的每个结点，δ(x, y) = 1如果x=y否则就是0。然后本文作者为了说明图核与本文的图卷积之间的联系，把卷积的公式改写为：

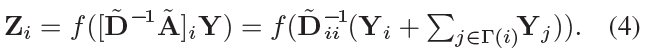
还说把Yi看成了结点i的颜色，并把这个公式看成是WL的“soft”版本。然而实际上Yi是一个特征向量，也就是例子中对应的整数“color”对应的连续的向量化的版本，所以我个人觉得本文的卷积操作还是和Kipf大佬的卷积操作更贴近。

Connection with propagation kernel

至于和第二个核propagation kernel（PK）之间的联系我就看得有点懵逼了，希望有看到这篇论文的大佬能在评论区里为我解答一下，由于我个人理解不到位所以我就在下面多抄一些原文。
P有一个传播规则：

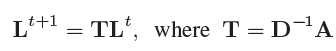
T=D^-1A是random walk的（概率）转移矩阵，Lt∈R^n×c包含了n个顶点在第t^th次迭代时的c维标签分布向量。在PK中，初始标签在迭代中扩散。最终的相似度是通过基于位置敏感哈希将所有迭代的分布向量映射到离散箱中，并计算公共整数箱。PK的图分类性能与WL相似，效率更高。这个装箱的操作应该就是对大概同范围的数值进行聚堆。

The SortPooling layer

排序池层的主要功能是对特征描述符进行排序，每个特征描述符代表一个顶点，在将它们放入传统的1-D卷积和Dense层之前，按照一致的顺序排序。其实最主要的问题就是根据什么排序。
还记得上文的卷积之后得到了Z^1:h:=[Z¹…Z^h]，用这个来对结点进行排序。它是几个不同的卷积层的输出拼接而成的，因此行表示结点，列表示特征通道。输出则是k×∑len(Z^t),也就是选取了topk作为输出，多截少补。
在排序的时候，先从最后一层GCN的输出开始比较，也就是Z^h，因为这个东西是由最多次卷积得到的，因此其特征更细粒度。假如两个结点的Z^h相同，那就再去比较Z^h-1，直到先后顺序确定为止。由于论文中为了与WL靠拢把这个比较成为颜色的比较，我觉得这个属实有点没必要，因为本质上就是按照大小进行的排序。我最终是看了github的源码才确定这一点的：

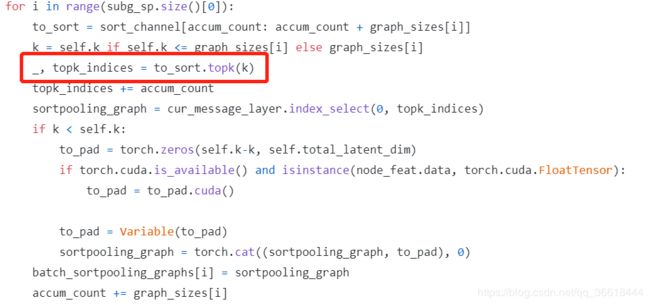
SortPooling作为图卷积层和传统层之间的桥梁，还有一个很大的好处，就是它可以通过记住输入的排序顺序，将损失梯度返回到前一层，使前一层参数的训练变得可行。相比之下，由于(Niepert, Ahmed, and Kutzkov 2016)在预处理步骤中对顶点进行排序，因此在排序之前不能进行参数训练。

Remaining layers

之后的操作就简便多了，先把池化之后的k个结点展开成行向量，之后进行1-D卷积，然后再给全连接层，最后输出分类数，就可以预测了。最终的模型架构长这样：

Experimental Results

实验评估了DGCNN与最先进的图核和其他深度学习方法对比的性能。