第四次周赛

YZJ的牛肉干

思路：
简单的递推一下以每一位字母结尾时候的符合要求的数量， fy[i]就表示以Y结尾时候长度为i的字符串有多少种， 同理，fz[i]表示以J结尾长度为i的字符串有多少种， fj[i]就是以Z结尾长度为i 的字符串有多少种。 那么 你就可以得到这么一个递推公式：

fy[i]=fy[i-1]+fz[i-1]+fj[i-1];
fz[i]=fy[i-1]+fj[i-1];
fj[i]=fy[i-1]+fz[i-1]+fj[i-1];

就以第一行为例，当第i位为Y时候，符合要求长度为i的字符串数量肯定等于分别以Y结尾长度为i-1的符 合要求字符串和以Z结尾长度为i-1的符合要求字符串数量，还有长度为i-1的以J结尾的符合要求字符串数 之和（仔细想想是不是这样），剩下两个也是相同的道理，只不过以Z结尾的时候不能再加上以Z结尾的 长度i-1的符合要求字符串，（不能出现ZZ)。 那么长度为n的符合要求字符串数量是不是就等于分别以这三个字母结尾的长度为n的字符串数量之 和。(注意这里数据范围超出int了，实际上40也超出long long范围了)
题解：

#include 
#include 
#include
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        long long i,fy[100],fz[100],fj[100];
        fy[1]=1;
        fz[1]=1;
        fj[1]=1;
        for(i=2; i<40; i++)
        {
            fy[i]=fy[i-1]+fz[i-1]+fj[i-1];
            fz[i]=fy[i-1]+fj[i-1];
            fj[i]=fy[i-1]+fz[i-1]+fj[i-1];
        }
        printf("%lld\n",fy[n]+fz[n]+fj[n]);
    }
    return 0;

扫雷

这道题又是四层for循环和二维数组的应用
代码：

#include 
#include 
#include
#include
int main()
{
    char a[1005][1005]={'\0'};
    int i,j,n,m,ii,jj;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
            scanf(" %c",&a[i][j]);
    }
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            int ans=0;
            for(ii=i-1;ii<i+2;ii++)
            {
                for(jj=j-1;jj<j+2;jj++)
                {
                    if(a[ii][jj]=='*')
                        ans++;
                }
            }
            if(a[i][j]=='*')printf("*");
            else printf("%d",ans);
        }
         printf("\n");
    }
    return 0;
}

签到题它又来了

这道题是结构体的应用，只不过多了一个去重和一个长宽的判定
代码

#include 
#include
#include
#include
#include
using namespace std;
struct people
{
    int c,k,bh;
} v[1005];
bool cmp(people x,people y)
{
    if(x.bh!=y.bh)
        return x.bh<y.bh;
    else if(x.c!=y.c)
        return x.c<y.c;
    else if(x.k!=y.k)
        return x.k<y.k;
}
int main()
{
    int n,m;
    int i;
    scanf("%d",&n);
    while (n--)
    {
    scanf("%d",&m);
        for(i=0; i<m; i++)
        {
            scanf("%d%d%d",&v[i].bh,&v[i].c,&v[i].k);
            int t;
            if(v[i].c<v[i].k)
            {
                t=v[i].c;
                v[i].c=v[i].k;
                v[i].k=t;
            }
        }
        sort(v,v+m,cmp);
        for(i=0; i<m; i++)
        {
            if(v[i-1].bh!=v[i].bh||v[i-1].c!=v[i].c||v[i-1].k!=v[i].k)
                printf("%d %d %d\n",v[i].bh,v[i].c,v[i].k);
        }
    }
    return 0;

万德隆购物

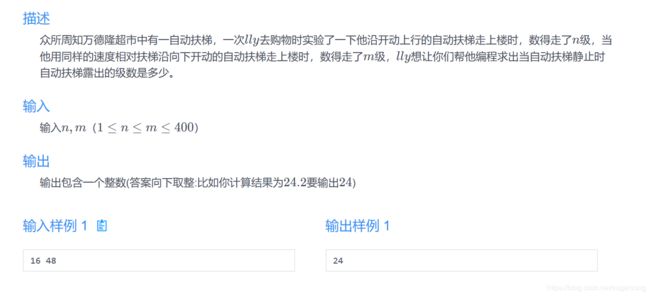
思路： 初中物理题，分析 和电梯在整个过程中的运动情况，电梯在整个运动过程中的速度不变，可以知道 向上和向下的运动时间之比为 。由人沿电梯上下行所走的路程相等，等于同一个楼层的高度， 建立方程即可求解：

代码：

#include 
#include 
#include
#include
int main()
{
    double n,m;
    scanf("%lf%lf",&n,&m);
    double a=(2.0*n*m)/(m+n);
    int b=a;
    printf("%d",b);
    return 0;
}

三生三世

题目比较长，大致意思就是说，输入两个字符串，判断他们的字符是否相同，但是他们还不能完全相同（本来我是用sort排序做的，没想到差点超时 -.- ）下面看一下统筹做法（这个做法挺快的，是sort的几百倍了0.0）
代码：

#include 
#include 
#include
#include
int main()
{
char a[200005],b[200005];
    int ak[2005]= {0},bk[2005]= {0},flog=0;
    int n,i;
    scanf("%d%s%s",&n,a,b);
    if(strcmp(a,b)==0)
        printf("no\n");
    else
    {
        for(i=0; i<n; ++i)
        {
            ak[a[i]-'A']++;
            bk[b[i]-'A']++;
        }
        for(i=0; i<='z'-'A'; ++i)
        {
            if(ak[i]!=bk[i])
            {
                printf("no\n");
                flog=1;
                break;
            }
        }
        if(flog==0)printf("yes\n");
    }
    return 0;
}

卖火柴的lly

思路：
既然是要找出形如A+B=C这样的等式，那最简单的办法就是分别枚举A，B，C。接下来的问题就是： A，B，C的枚举范围是什么呢？我们只需要在0～1111之间枚举就可以了。为什么呢？因为题目中最多 只有24根火柴棒即m<=24。除去“+”和“-”占用的4根火柴棍，那么最多剩下20根火柴棍。而0-9这十个数 字中，1需要用到的火柴棍最少，只需要2根火柴棍。而20根火柴棍最多能组成10个1。因此A+B=C这个 等式中A,B,C中任意一个数都不能超过1111。接下来就暴力求解就阔以了。
代码：

#include 
#include 
#include
#include
int write(int x)
{
    int ans=0,f[10]={6,2,5,5,4,5,6,3,7,6};
    while (x/10!=0)
     {
        ans+=f[x%10];
        x/=10;
    }
    ans+=f[x];
    return ans;
}
int main()
{
    int n,a,b,c,ans=0;
    scanf("%d",&n);
    for(a=0;a<1111;a++)
    {
        for(b=0;b<1111;b++)
        {
            c=a+b;
            if(write(a)+write(b)+write(c)==n-4)
                ans++;
        }
    }
    printf("%d",ans);
    return 0;
}

进位

就是简单的加法，注意保留一下进位就行了（可以参考一下大数加法）
代码：

#include 
#include 
#include
#include
int main()
{
    char a[5],b[5];
    while (~scanf("%s%s",a,b))
    {
        int i,ans=0,t=0;
        if(a[0]=='0'&&b[0]=='0')
            break;
        for(i=2; i>=0; i--)
        {
            t=(a[i]-'0'+b[i]-'0'+t);
            if(t>=10)ans++;
            t/=10;
        }
         printf("%d\n",ans);
    }
    return 0;
}

最直接的题

仔细思考一下就可以很快想到思路了，其实就是找奇数和偶数的最小值
代码：

#include 
#include 
#include
#include
int main()
{
    int n,a=0,b=0,i,m;
    scanf("%d",&n);
    for(i=0;i<n;i++)
    {
        scanf("%d",&m);
        if(m%2==0)
            a++;
        else b++;
    }
    if(a>=b)printf("%d",b);
    else printf("%d",a);
    return 0;
}

淘宝盖楼

学姐又开始盖楼了，你们的等级都是多少呢？快来帮助学姐吧！（虽然双十一已经结束了QAQ），大家是不是都已经开始吃土了呢
代码：

#include 
#include 
#include
int main()
{
    int n,i,maxi=-100;
    long long ans=0,a;
    scanf("%d",&n);
    for(i=0;i<n;i++)
    {
        scanf("%lld",&a);
         if(a>=maxi)
         {
             maxi=a;
             ans+=maxi;
         }
    }
    printf("%lld",ans);
    return 0;
}

Belief

直接看代码吧

#include 
#include 
#include
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        printf("I love ACM,ACM is my belief!\n");
    }
    return 0;
}

爱我中华

直接看代码，还是签到题
代码

#include 
#include 
#include
int main()
{
    int n;
    scanf("%d",&n);
    printf("%d",1949+n);
    return 0;
}

货车

这是栈的应用，不算太难，会用就能解
代码：

#include 
#include
#include
#include
#include
using namespace std;
int main()
{
    int a,i,n,j,m;
    stack<int>q;
    scanf("%d%d",&n,&m);
     for(i=1; i<=n; i++)
    {
//        scanf("%d",&a);
        q.push(i);
    }
    for(i=1; i<=m; i++)
    {
        scanf("%d",&j);
        if(j==1)
        {
            scanf("%d",&a);
            q.push(a);
        }
        else
        {
            if(!q.empty())
            {
               q.pop();
            }
        }
    }
    if(q.empty())
        printf("NO\n");
    else
    {
        while(!q.empty())
        {
            int x=q.top();
            q.pop();
            printf("%d",x);
            printf(" ");
        }
    }
    return 0;
}